Hierbei handelt es sich um eine Methode zum Beibehalten des simultanen Konfidenzniveaus für eine ganze Gruppe von Konfidenzintervallen. Wenn Sie mehrere Konfidenzintervalle untersuchen, ist es wichtig, das simultane Konfidenzniveau zu berücksichtigen, weil die Wahrscheinlichkeit, dass mindestens eines der Konfidenzintervalle den Parameter der Grundgesamtheit nicht enthält, bei einer Reihe von Intervallen größer als bei einem einzelnen Intervall ist. Um dieser höheren Irrtumswahrscheinlichkeit zu begegnen, korrigiert die Bonferroni-Methode das Konfidenzniveau für jedes einzelne Intervall, so dass das resultierende simultane Konfidenzniveau dem angegebenen Wert entspricht.
Beispiel für Bonferroni-Konfidenzintervalle
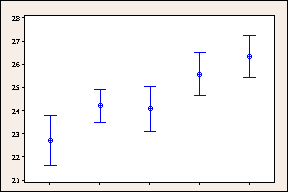
Nicht korrigierte 95%-Konfidenzintervalle für Lieferzeiten nach Versandzentrum
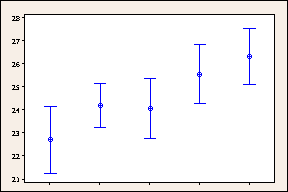
95%-Bonferroni-Konfidenzintervalle für Lieferzeiten nach Versandzentrum (individuelle 99%-Konfidenzintervalle)
In diesen Grafiken werden normale 95%-Konfidenzintervalle mit 95%-Bonferroni-Konfidenzintervallen verglichen. Die breiteren Bonferroni-Konfidenzintervalle bieten weniger genaue Schätzwerte des Parameters der Grundgesamtheit, doch senken sie die Wahrscheinlichkeit, dass mindestens ein Konfidenzintervall den Parameter nicht enthält, auf maximal 5 %. Im Vergleich beläuft sich die simultane Irrtumswahrscheinlichkeit für die fünf regulären 95%-Konfidenzintervalle auf 25 %.
Diese konservative Methode stellt sicher, dass das Gesamtkonfidenzniveau mindestens 1–α beträgt. Um für die gemeinsamen Intervallschätzwerte ein Gesamtkonfidenzniveau von 1–α zu erhalten, erstellt Minitab jedes Intervall mit einem Konfidenzniveau von (1–α/g), wobei g die Anzahl der Intervalle angibt. In den Bonferroni-Intervallen verwendet Minitab 99%-Konfidenzintervalle (1,00–0,05/5 = 0,99), um das simultane 95%-Konfidenzniveau zu erhalten.
