Was ist eine MANOVA (multivariate Varianzanalyse)?
- Erhöhte Trennschärfe
- Mit Hilfe der Kovarianzstruktur der Daten zwischen den Antwortvariablen können Sie gleichzeitig die Gleichheit der Mittelwerte testen. Wenn die Antwortvariablen korreliert sind, können diese Zusatzinformationen beim Ermitteln von Unterschieden helfen, die zu klein sind, um bei einzelnen ANOVAs erkannt zu werden.
- Erkennung von multivariaten Mustern in den Werten der Antwortvariablen
- Die Faktoren wirken sich u. U. auf die Beziehung zwischen den Antwortvariablen und nicht nur auf eine einzelne Antwortvariable aus. Mit ANOVAs werden diese multivariaten Muster nicht erkannt, wie in den folgenden Abbildungen veranschaulicht wird.
- Kontrolle der simultanen Irrtumswahrscheinlichkeit
- Die Wahrscheinlichkeit, dass die Nullhypothese fälschlicherweise zurückgewiesen wird, steigt mit jeder nachfolgenden ANOVA. Durch das Ausführen einer MANOVA zum gleichzeitigen Testen aller Antwortvariablen wird die simultane Irrtumswahrscheinlichkeit auf dem Alpha-Niveau gehalten.
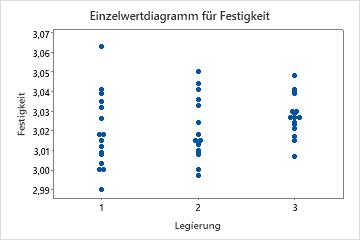
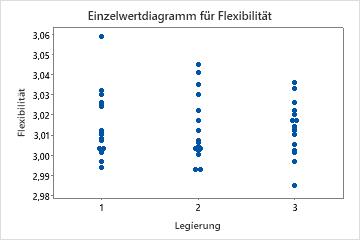
Angenommen, Sie untersuchen die Auswirkungen verschiedener Legierungen (1, 2 und 3) auf die Festigkeit und Flexibilität der Baustoffprodukte Ihres Unternehmens. Zuerst führen Sie getrennte ANOVAs durch, doch die Ergebnisse sind nicht signifikant. Dies überrascht Sie, und Sie tragen die Rohdaten für beide Antwortvariablen in Einzelwertdiagrammen auf. Diese Diagramme bestätigen die fehlende Signifikanz der ANOVA-Ergebnisse.
Da die Antwortvariablen korreliert sind, führen Sie eine MANOVA durch. Dieses Mal sind die Ergebnisse mit p-Werten unter 0,05 signifikant. Sie erstellen ein Streudiagramm, um die Ergebnisse besser zu verstehen.
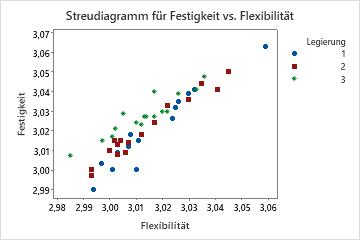
Die Einzelwertdiagramme zeigen aus univariater Perspektive, dass die Legierungen weder die Festigkeit noch die Flexibilität signifikant beeinflussen. Das Streudiagramm für dieselben Daten zeigt jedoch, dass die verschiedenen Legierungen die Beziehungen zwischen den beiden Antwortvariablen ändern. Das heißt, bei einem angegebenen Flexibilitätswert besitzt Legierung 3 im Allgemeinen einen höheren Festigkeitswert als die Legierungen 1 und 2. Mit einer MANOVA können multivariate Antwortvariablen dieses Typus erkannt werden, mit einer ANOVA jedoch nicht.
Hinweis
Im Allgemeinen sollten Sie die Daten grafisch darstellen, bevor Sie eine Analyse durchführen, um leichter entscheiden zu können, welche Vorgehensweise geeignet ist.
Welche multivariaten Tests sind in der MANOVA enthalten?
- Wilk-Test
- Lawley-Hotelling-Test
- Pillai-Test
- Größte charakteristische Wurzel nach Roy
- Eine mit den einzelnen Termen verknüpfte H-Matrix (Hypothesenmatrix), die auch als Summe der Quadrate zwischen den Stichproben bezeichnet wird
- Eine mit dem Fehler für den Test verknüpfte E-Matrix (Fehlermatrix), die auch als Summe der Quadrate innerhalb der Stichprobe bezeichnet wird
Die SSCP-Matrizen werden angezeigt, wenn Sie die Hypothesenmatrizen anfordern.
Sie können die Teststatistiken entweder als H, E oder H und E oder als Eigenwerte von E-1 H ausdrücken. Sie können festlegen, dass diese Eigenwerte angezeigt werden sollen. (Wenn die Eigenwerte wiederholt werden, sind die entsprechenden Eigenvektoren nicht eindeutig. In diesem Fall stimmen die Eigenvektoren, die von Minitab angezeigt werden, und die, die in Büchern und anderer Software angezeigt werden, möglicherweise nicht überein. Die MANOVA-Tests sind jedoch immer eindeutig.)
