Was ist eine Kovariate?
Kovariaten kommen im Allgemeinen in der ANOVA und der Versuchsplanung zur Anwendung. In diesen Modellen ist eine Kovariate eine stetige Variable, die während der Datenerfassung im Allgemeinen nicht kontrolliert wird. Das Einbinden von Kovariaten ermöglicht das Modellieren von und Anpassen für Eingabevariablen, die zwar erfasst, jedoch im Experiment weder randomisiert noch kontrolliert wurden. Durch Hinzufügen von Kovariaten können Sie die Genauigkeit des Modells erheblich steigern; zudem können sich diese wesentlich auf die endgültigen Ergebnisse der Analyse auswirken. Das Einbinden einer Kovariate in das Modell kann den Fehler im Modell verringern und somit die Trennschärfe der Faktortests erhöhen. Zu den üblichen Kovariaten gehören Umgebungstemperatur, Luftfeuchtigkeit sowie Merkmale eines Teils oder Prüfobjekts vor der Behandlung.
Ein Techniker möchte beispielsweise den Korrosionsgrad bei vier Typen von Eisenträgern untersuchen. Der Techniker unterzieht die Eisenträger jeweils einer Behandlung mit Flüssigkeit, um die Korrosion zu beschleunigen, kann aber die Temperatur der Flüssigkeit nicht kontrollieren. Die Temperatur ist eine Kovariate, die im Modell berücksichtigt werden sollte.
In der Versuchsplanung kann ein Ingenieur beispielsweise am Effekt der Kovariate Umgebungstemperatur auf die Trockenzeit zweier unterschiedlicher Lacktypen interessiert sein.
Beispiel für das Hinzufügen einer Kovariate zu einem allgemeinen linearen Modell
Ein Textilunternehmen verwendet für die Produktion von monofilen Fäden drei unterschiedliche Maschinen. Es soll bestimmt werden, ob die Reißfestigkeit der Fäden abhängig von der verwendeten Maschine variiert. Es werden Daten zu Festigkeit und Durchmesser von 5 zufällig ausgewählten Fäden von jeder Maschine erfasst. Da die Festigkeit der Fäden im Zusammenhang mit ihrem Durchmesser steht, wird auch der Fadendurchmesser als mögliche Kovariate aufgezeichnet.
| C1 | C2 | C3 |
|---|---|---|
| Maschine | Durchmesser | Festigkeit |
| 1 | 20 | 36 |
| 1 | 25 | 41 |
| 1 | 24 | 39 |
| 1 | 25 | 42 |
| 1 | 32 | 49 |
| 2 | 22 | 40 |
| 2 | 28 | 48 |
| 2 | 22 | 39 |
| 2 | 30 | 45 |
| 2 | 28 | 44 |
| 3 | 21 | 35 |
| 3 | 23 | 37 |
| 3 | 26 | 42 |
| 3 | 21 | 34 |
| 3 | 15 | 32 |
- Überprüfen Sie, ob eine lineare Beziehung zwischen der Kovariate und der Antwortvariablen besteht. Sie können dies in Minitab durch das Analysieren der Daten mit einer Darstellung der Anpassungslinie durchführen.
- Wählen Sie aus.
- Geben Sie im Feld Antwort (Y) die Variable Festigkeit ein.
- Geben Sie im Feld Prädiktor (X) die Variable Durchmesser ein.
- Bestimmen Sie die Nähe der Daten zur Anpassungslinie und die Nähe von R2 zu einer perfekten Anpassung (100 %).
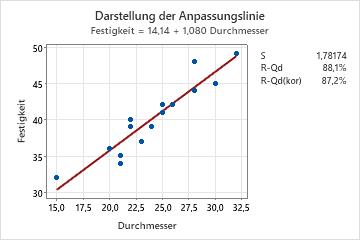
Die Darstellung der Anpassungslinie zeigt eine starke lineare Beziehung (87,2 %) zwischen Durchmesser und Festigkeit.
- Führen Sie die GLM-Analyse mit der Kovariate durch.
- Wählen Sie aus.
- Geben Sie im Feld Antworten die Variable Festigkeit ein.
- Geben Sie im Feld Faktoren die Variable Maschine ein.
- Geben Sie im Feld Kovariaten die Variable Durchmesser ein.
- Klicken Sie auf OK.
Minitab zeigt die folgenden Ergebnisse für die Daten zur Fadenproduktion an:
Allgemeines lineares Modell: Festigkeit vs. Durchmesser; Maschine
Varianzanalyse Quelle DF Kor SS Kor MS F-Wert p-Wert Durchmesser 1 178,014 178,014 69,97 0,000 Maschine 2 13,284 6,642 2,61 0,118 Fehler 11 27,986 2,544 Fehlende Anpassung 7 18,486 2,641 1,11 0,487 Reiner Fehler 4 9,500 2,375 Gesamt 14 346,400Die F-Statistik für die Maschinen beträgt 2,61, und der p-Wert beträgt 0,118. Da der p-Wert größer als 0,05 ist, weisen Sie die Nullhypothese, dass sich die Fadenfestigkeit abhängig von der verwendeten Maschine nicht unterscheidet, bei einem Signifikanzniveau von 5 % nicht zurück. Sie können annehmen, dass die Fadenfestigkeit bei allen Maschinen gleich ist. Beachten Sie, dass die F-Statistik für den Durchmesser (Kovariate) 69,97 und der entsprechende p-Wert 0,000 beträgt. Dies bedeutet, dass ein signifikanter Kovariateneffekt vorliegt. Somit hat der Durchmesser einen statistisch signifikanten Einfluss auf die Fadenfestigkeit.
Angenommen, Sie führen die Analyse nun erneut aus, jedoch ohne die Kovariate. Sie erhalten dann die folgende Ausgabe:
Allgemeines lineares Modell: Festigkeit vs. Maschine
Varianzanalyse Quelle DF Kor SS Kor MS F-Wert p-Wert Maschine 2 140,4 70,20 4,09 0,044 Fehler 12 206,0 17,17 Gesamt 14 346,4Beachten Sie, dass die F-Statistik 4,09 und der p-Wert 0,044 beträgt. Ohne die Kovariate im Modell verwerfen Sie die Nullhypothese bei einem Signifikanzniveau von 5 % und schlussfolgern, dass die Fadenfestigkeit abhängig von der verwendeten Maschine variiert.
Diese Schlussfolgerung ist das Gegenteil der Schlussfolgerung aus der Analyse mit der Kovariate. Dieses Beispiel zeigt, dass das Weglassen einer Kovariate zu irreführenden Analyseergebnissen führen kann.
