Informationen über die Meldung zu einem Rangdefizit
Lineare Modelle haben einen vollen Rang, wenn für jede Kombination von Faktorstufen eine ausreichende Anzahl von Beobachtungen vorhanden ist, um sämtliche im Modell eingebundenen Terme zu schätzen. Wenn die Anzahl der Beobachtungen in den Daten nicht ausreicht, um das Modell anzupassen, entfernt Minitab Terme, bis das Modell klein genug für eine Anpassung ist. Möglicherweise sind andere Modelle besser angepasst.
Angenommen, Sie verfügen über ein GLM-Modell mit zwei Faktoren. Sie versuchen, das Modell mit den Termen A, B und A*B anzupassen, und erhalten eine Fehlermeldung über ein Rangdefizit. Dies deutet darauf hin, dass nicht genügend Beobachtungen pro Kombination von Faktorstufen vorhanden sind. In diesem Fall könnten Sie versuchen, den Wechselwirkungsterm (A*B) zu entfernen.
Was ist ein Rangdefizit?
Ein Rangdefizit kann das Durchführen von Matrixberechnungen durch Minitab verhindern. Betrachten Sie beispielsweise den folgenden Datensatz mit zwei Prädiktorvariablen und einer Antwortvariablen:
| C1 | C2 | C3 |
|---|---|---|
| X1 | X2 | Y |
| 1,5 | 9,7 | 15,0 |
| 1,4 | 8,4 | 14,0 |
| 1,6 | 8,6 | 16,0 |
| 1,7 | 8,9 | 17,0 |
| 1,7 | 8,1 | 14,5 |
x1 und x2 sind die Prädiktorvariablen, und y ist die Antwortvariable. Bei der Regressionsanalyse in Minitab werden die Schätzwerte der Koeffizienten b0, b1, b2 in der folgenden linearen Gleichung mit Hilfe der kleinsten Quadrate berechnet:
y = b0 + b1x1 + b2x2
Das Verfahren der kleinsten Quadrate entspricht dem Lösen der Gruppe von Matrixgleichungen
b = (XTX)–1XTY
Dabei ist b ein Spaltenvektor, der die geschätzten Modellkoeffizienten enthält, X ist eine Matrix, deren erste Spalte jeweils den Wert 1 enthält (zum Schätzen des Schnittpunkts mit der y-Achse/Konstanten) und deren restliche Spalten die Prädiktordaten (X1, X2, …) enthalten, und Y ist der Spaltenvektor der Antwortdaten. Die Matrizen für den vorherigen Datensatz lauten:
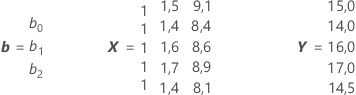
Minitab berechnet die Schätzwerte der Parameter (b0, b1 und b2) und die Standardabweichung der Parameter mit Hilfe der QR-Zerlegung. Die Berechnung hängt von den Eigenwerten der Matrix (XTX) ab. Wenn einige der Eigenwerte von (XTX) im Wesentlichen null betragen, ist die quadratische Matrix (XTX) entweder singulär oder nahezu singulär, und Minitab kann die Berechnungen nicht durchführen.
Was verursacht ein Rangdefizit?
Ein Rangdefizit tritt auf, wenn x-Variablenspalten als lineare Kombination der anderen x-Spalten geschrieben werden können. Es werden zwei Beispiele gezeigt, in denen C1, C2 und C3 als Prädiktorvariablen (x) verwendet werden:
Beispiel 1
| C1 | C2 | C3 |
|---|---|---|
| X1 | X2 | X3 |
| 1 | 2 | 3 |
| 2 | 3 | 5 |
| 1,5 | 2,5 | 4 |
Beispiel 2
| C1 | C2 | C3 |
|---|---|---|
| X1 | X2 | X3 |
| 1 | 2 | 3 |
| 2 | 4 | 5 |
| 1,5 | 3 | 4 |
Beachten Sie im ersten Beispiel, dass C1 + C2 = C3.
Beachten Sie im zweiten Beispiel, dass 2*C1 = C2.
Wenn Sie versuchen, mit diesen Prädiktoren eine Regression (oder ANOVA) auszuführen, entfernt Minitab Terme aus dem Modell, um die Analyse durchzuführen.
Ein Rangdefizit kann auch bei kategorialen Daten auftreten:
Beispiel 3
| C1 | C2 | C3 |
|---|---|---|
| Maschine | Prüfer | Antwort |
| 1 | Jürgens | 15 |
| 1 | Jürgens | 18 |
| 1 | Jürgens | 17 |
| 2 | Baumann | 14 |
| 2 | Baumann | 15 |
| 2 | Baumann | 16 |
In diesem Beispiel weist die Spalte „Maschine“ genau das gleiche Muster wie die Spalte „Bediener“ auf. Wenn Sie mit diesem Datensatz eine ANOVA durchführen, entfernt Minitab Terme aus dem Modell, um die Analyse durchzuführen.
- Ein enthaltener Wechselwirkungsterm weist nicht mindestens eine Beobachtung für jede Kombination von Faktorstufen auf. Beispiel: A verfügt über 3 Stufen, B verfügt über 4 Stufen, und Sie nehmen die Wechselwirkung A*B in das Modell auf, ohne dass mindestens eine Beobachtung für jede der 12 Kombinationen von Faktorstufen vorliegt.
- Es liegt eine nicht balancierte Schachtelung vor.
- Eine stetige Variable im Modell ist nicht als Kovariate angegeben.
- Die Freiheitsgrade für Fehler sind negativ.
