In diesem Thema
Mehrfachvergleichstest
Intervalle für Mehrfachvergleiche für k > 2 Stichproben
Sei 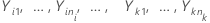 k > 2 unabhängige Stichproben, jeweils unabhängig und identisch verteilt mit dem Mittelwert
k > 2 unabhängige Stichproben, jeweils unabhängig und identisch verteilt mit dem Mittelwert 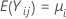 und der Varianz
und der Varianz  . Sei außerdem angenommen, dass die Stichproben aus Grundgesamtheiten mit einer gemeinsamen Kurtosis stammen.
. Sei außerdem angenommen, dass die Stichproben aus Grundgesamtheiten mit einer gemeinsamen Kurtosis stammen. 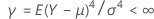
Des Weiteren sei 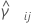 ein Schätzwert der zusammengefassten Kurtosis für das Paar von Stichproben (i, j), das wie folgt gegeben wird:
ein Schätzwert der zusammengefassten Kurtosis für das Paar von Stichproben (i, j), das wie folgt gegeben wird:
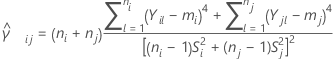
Sei 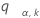 der obere a-Punkt der Spannweite von k Variablen, die unabhängig und gemäß einer zufälligen Standardnormalverteilung identisch verteilt sind. Das heißt,
der obere a-Punkt der Spannweite von k Variablen, die unabhängig und gemäß einer zufälligen Standardnormalverteilung identisch verteilt sind. Das heißt, 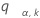 erfüllt folgende Bedingungen:
erfüllt folgende Bedingungen:
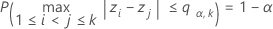
Hierbei sind Z1, ..., Zk unabhängige und gemäß einer Standardnormalverteilung identisch verteilte Zufallsvariablen. Barnard (1978) gibt einen einfachen numerischen Algorithmus an, der auf einer Gaußschen Quadratur von 16 Punkten zum Berechnen der Verteilungsfunktion über die Spannweite der Normalverteilung basiert.
Beim Mehrfachvergleichsverfahren wird die Nullhypothese der Gleichheit der Varianzen (auch als Homogenität der Varianzen bezeichnet) nur dann zurückgewiesen, wenn mindestens ein Paar der folgenden Intervalle keine Überlappung aufweist:
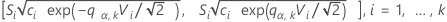
Dabei gilt Folgendes:
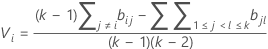
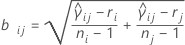
wobei ri = (ni – 3) / ni.
Die oben aufgeführten Intervalle werden als Mehrfachvergleichsintervalle oder MV-Intervalle bezeichnet. Die MV-Intervalle für die einzelnen Stichproben dürfen nicht als Konfidenzintervalle für die Standardabweichungen der übergeordneten Grundgesamtheiten interpretiert werden. Hochberg et al. (1982) bezeichnen ähnliche Intervalle für Vergleiche von Mittelwerten als „Unsicherheitsintervalle“. Die hier angegebenen MV-Intervalle sind nur nützlich bei Vergleichen der Standardabweichungen bzw. Varianzen für Designs mit mehreren Stichproben. Wenn der Mehrfachvergleichstest insgesamt signifikant ist, unterscheiden sich die Standardabweichungen, die den einander nicht überlappenden Intervallen entsprechen, statistisch voneinander. (Eine ausführliche Ableitung dieser Intervalle finden Sie im White Paper zu Methoden für Mehrfachvergleiche.)
Intervalle für Mehrfachvergleiche für k = 2 Stichproben
Wenn lediglich zwei Stichproben vorhanden sind, werden die Intervalle für die Mehrfachvergleiche wie folgt ausgedrückt:

Hierbei ist zα / 2 der obere (α / 2)-Perzentilpunkt der Standardnormalverteilung, ci = ni / ni – zα / 2, und Vi wird mit der folgenden Formel angegeben:
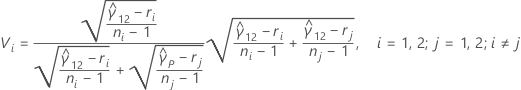
p-Wert für den Test
Wenn zwei Stichproben im Design vorhanden sind, berechnet Minitab den p-Wert für den Mehrfachvergleichstest mit der Bonett-Methode für einen Test auf Varianzen bei zwei Stichproben und einem hypothetischen Verhältnis Ρo von 1.
Wenn k > 2 Stichproben im Design vorhanden sind, sei Pi j der p-Wert des Tests für ein Paar (i, j) von Stichproben. Der p-Wert für das Mehrfachvergleichsverfahren als Gesamttest auf Gleichheit der Varianzen wird mit folgender Formel angegeben:

Weitere Informationen, u. a. Simulationen und detaillierte Algorithmen zum Berechnen von Pi j, finden Sie in Bonett-Methode, einem White Paper mit Simulationen und sonstigen Informationen zur Bonett-Methode.
Notation
| Begriff | Beschreibung |
|---|---|
| ni | Anzahl der Beobachtungen in der Stichprobe i |
| Y i l | l-te Beobachtung in Stichprobe i |
| mi | getrimmtes Mittel für die Stichprobe i mit getrimmten Anteilen von  |
| k | Anzahl der Stichproben |
| Si | Standardabweichung von Stichprobe i |
| α | Signifikanzniveau für den Test = 1 – (Konfidenzniveau/100) |
| Ci | 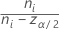 |
| Zα / 2 | oberer (α / 2)-Perzentilpunkt der Standardnormalverteilung |
| ri |  |
Levene-Teststatistik
Minitab zeigt eine Teststatistik und einen p-Wert für den Levene-Test an. Die Nullhypothese besagt, dass die Varianzen gleich sind, während die Alternativhypothese besagt, dass die Varianzen ungleich sind. Verwenden Sie den Levene-Test, wenn die Daten zwar aus stetigen, aber nicht unbedingt aus normalverteilten Stichproben stammen.
Die Berechnungsmethode für den Levene-Test ist eine Abwandlung des Levene-Verfahrens (Levene, 1960), die von Brown und Forsythe (1974) entwickelt wurde. Diese Methode berücksichtigt die Distanzen der Beobachtungen von ihrem Stichprobenmedian statt ihrem Stichprobenmittelwert. Da sich der Test auf den Stichprobenmedian und nicht auf den Stichprobenmittelwert stützt, ist er robuster bei kleineren Stichproben, und das Verfahren ist asymptotisch verteilungsfrei. Wenn der p-Wert kleiner als das α-Niveau ist, verwerfen Sie die Nullhypothese, dass die Varianzen gleich sind.
Formel
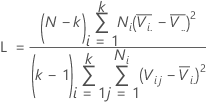
- H. Levene (1960). Contributions to Probability and Statistics. Stanford University Press, CA.
- M. B. Brown and A. B. Forsythe (1974). „Robust tests for the equality of variance“, Journal of the American Statistical Association, 69, 364-367.
Notation
| Begriff | Beschreibung |
|---|---|
| Vij |  |
| i | 1, ..., k |
| j | 1, ..., ni |
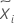 | Median |
Bartlett-Teststatistik
Minitab zeigt eine Teststatistik und einen p-Wert für den Bartlett-Test an. Wenn nur zwei Stufen vorhanden sind, führt Minitab anstelle des Bartlett-Tests einen F-Test durch. Für diese Tests besagt die Nullhypothese, dass die Varianzen gleich sind, während die Alternativhypothese besagt, dass die Varianzen ungleich sind. Verwenden Sie einen Bartlett-Test, wenn die Daten aus Normalverteilungen stammen. Der Bartlett-Test ist gegenüber Abweichungen von der Normalverteilung nicht robust.
Mit der Bartlett-Teststatistik werden der gewichtete arithmetische Durchschnitt und der gewichtete geometrische Durchschnitt der einzelnen Stichprobenvarianzen auf der Grundlage der Freiheitsgrade berechnet. Je größer die Differenz in den Durchschnitten, desto wahrscheinlicher ist es, dass die Varianzen der Stichproben ungleich sind. B folgt einer χ2-Verteilung mit k–1 Freiheitsgraden. Wenn der p-Wert kleiner als das α-Niveau ist, verwerfen Sie die Nullhypothese, dass die Varianzen gleich sind.
Formel
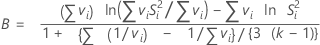
Notation
| Begriff | Beschreibung |
|---|---|
| si2 |  |
| k | Anzahl der Stichproben |
| vi | ni – 1 |
| ni | Anzahl der Beobachtungen auf der i-ten Faktorstufe |
F-Teststatistik
Wenn nur zwei Stufen vorhanden sind, führt Minitab anstelle des Bartlett-Tests einen F-Test durch. Die Nullhypothese besagt, dass die Varianzen gleich sind, während die Alternativhypothese besagt, dass die Varianzen ungleich sind. Verwenden Sie die F-Statistik, wenn die Daten aus Normalverteilungen stammen.
Wenn der p-Wert kleiner als das α-Niveau ist, verwerfen Sie die Nullhypothese, dass die Varianzen gleich sind.
Formel
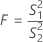
Formel für p-Wert
- Für einen einseitigen Test mit einer „Kleiner als“-Alternativhypothese entspricht der p-Wert der Wahrscheinlichkeit, eine F-Statistik zu erhalten, die kleiner oder gleich dem beobachteten Wert aus einer F-Verteilung mit DF1 und DF2 Freiheitsgraden ist.
- Für einen beidseitigen Test mit einem Verhältnis kleiner als 1 entspricht der p-Wert dem Zweifachen der Fläche unter der F-Kurve bis zu dem beobachteten Wert aus einer F-Verteilung mit DF1 und DF2 Freiheitsgraden.
- Für einen beidseitigen Test mit einem Verhältnis größer als 1 entspricht der p-Wert dem Zweifachen der Fläche unter der F-Kurve ab dem beobachteten Wert aus einer F-Verteilung mit DF1 und DF2 Freiheitsgraden.
- Für einen einseitigen Test mit einer „Größer als“-Alternativhypothese entspricht der p-Wert der Wahrscheinlichkeit, eine F-Statistik zu erhalten, die größer oder gleich dem beobachteten Wert aus einer F-Verteilung mit DF1 und DF2 Freiheitsgraden ist.
Notation
| Begriff | Beschreibung |
|---|---|
| S12 | Varianz der Stichprobe 1 |
| S22 | Varianz der Stichprobe 2 |
| n1 – 1 | Freiheitsgrade des Zählers |
| n2 – 1 | Freiheitsgrade des Nenners |
Standardabweichung (StdAbw)
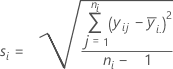
Notation
| Begriff | Beschreibung |
|---|---|
| yij | Beobachtungen auf der i-ten Faktorstufe |
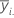 | Mittelwert der Beobachtungen auf der i-ten Faktorstufe |
| ni | Anzahl der Beobachtungen auf der i-ten Faktorstufe |
Bonferroni-Konfidenzintervalle
Minitab berechnet die Konfidenzintervalle für die Standardabweichungen mit der Bonferroni-Methode. Ein Konfidenzintervall ist ein Bereich von Werten, der wahrscheinlich einen Parameter der Grundgesamtheit enthält; in diesem Fall handelt es sich um die Standardabweichung.
Reguläre Konfidenzintervalle werden mit einem Konfidenzniveau von 1–α/2 berechnet. Bei der Bonferroni-Methode wird hingegen das Konfidenzniveau 1–α/2p für jedes individuelle Konfidenzintervall verwendet, wobei p die Anzahl der Faktor- und Stufenkombinationen angibt. Mit der Methode wird sichergestellt, dass die Gesamtheit der Konfidenzintervalle ein Konfidenzniveau von mindestens 1–α aufweist. Die Bonferroni-Methode liefert konservativere (breitere) Konfidenzintervalle, wodurch die Wahrscheinlichkeit eines Fehlers 1. Art gemindert wird.
