In diesem Thema
Nullhypothese, Alternativhypothese
Der Test auf gleiche Varianzen ist ein Hypothesentest, bei dem zwei einander ausschließende Aussagen über mindestens zwei Standardabweichungen einer Grundgesamtheit auswertet werden. Diese beiden Aussagen werden als Nullhypothese und Alternativhypothese bezeichnet. In einem Hypothesentest werden Stichprobendaten verwendet, um zu bestimmen, ob die Nullhypothese zurückgewiesen werden sollte.
- Nullhypothese (H0)
- Die Nullhypothese besagt, dass alle Standardabweichungen der Grundgesamtheiten gleich sind.
- Alternativhypothese (HA)
- Die Alternativhypothese besagt, dass nicht alle Standardabweichungen der Grundgesamtheiten gleich sind.
Interpretation
Vergleichen Sie den p-Wert mit dem Signifikanzniveau, um festzustellen, ob die Nullhypothese zurückgewiesen werden sollte.
N
Der Stichprobenumfang (N) gibt die Gesamtzahl der Beobachtungen in jeder Gruppe an.
Interpretation
Der Stichprobenumfang wirkt sich auf das Konfidenzintervall und auf die Trennschärfe des Tests aus.
Eine größere Stichprobe führt in der Regel zu einem schmaleren Konfidenzintervall. Bei größeren Stichprobenumfängen verfügt der Test außerdem über eine höhere Trennschärfe zum Erkennen einer Differenz.
Standardabweichung (StdAbw)
Die Standardabweichung ist das am häufigsten verwendete Maß für die Streuung bzw. die Streubreite der Daten um den Mittelwert. Die Standardabweichung einer Grundgesamtheit wird oft mit dem Symbol σ (Sigma) dargestellt. Die Standardabweichung einer Stichprobe wird hingegen mit dem Buchstaben s dargestellt.
Interpretation
Für die Standardabweichung wird die gleiche Einheit wie für die Variable verwendet. Ein höherer Wert der Standardabweichung verweist auf eine größere Streubreite der Daten. Eine Faustregel für normalverteilte Daten besagt, dass etwa 68 % der Werte innerhalb einer Standardabweichung vom Mittelwert, 95 % der Werte innerhalb von zwei Standardabweichungen und 99,7 % der Werte innerhalb von drei Standardabweichungen liegen.
Bonferroni-Konfidenzintervalle
Verwenden Sie die Bonferroni-Konfidenzintervalle, um die Standardabweichung jeder Grundgesamtheit auf der Grundlage der kategorialen Faktoren zu schätzen. Jedes Konfidenzintervall ist ein Bereich von Werten, der wahrscheinlich die Standardabweichung der entsprechenden Grundgesamtheit enthält. Minitab korrigiert die Bonferroni-Konfidenzintervalle, um das simultane Konfidenzniveau beizubehalten.
Das Beibehalten des simultanen Konfidenzniveaus ist insbesondere dann wichtig, wenn mehrere Konfidenzintervalle untersucht werden. Wenn das simultane Konfidenzniveau nicht beibehalten wird, erhöht sich mit zunehmender Anzahl von Konfidenzintervallen die Wahrscheinlichkeit, dass mindestens ein Konfidenzintervall nicht die tatsächliche Standardabweichung enthält.
Weitere Informationen finden Sie unter Grundlagen von individuellen und simultanen Konfidenzniveaus in Mehrfachvergleichen und Was ist die Bonferroni-Methode?
Hinweis
Mit den Bonferroni-Konfidenzintervallen können Sie nicht ermitteln, ob die Differenzen zwischen Paaren von Gruppen statistisch signifikant sind. Verwenden Sie die p-Werte und die Konfidenzintervalle für Mehrfachvergleiche im zusammenfassenden Diagramm, um die statistische Signifikanz der Differenzen zu ermitteln.
Interpretation
Methode
| Nullhypothese | Alle Varianzen sind gleich. |
|---|---|
| Alternativhypothese | Mindestens eine Varianz weicht ab. |
| Signifikanzniveau | α = 0,05 |
95%-Bonferroni-KIs für Standardabweichungen
| Dünger | N | StdAbw | KI |
|---|---|---|---|
| GrowFast | 50 | 4,28743 | (3,43659; 5,61790) |
| Keiner | 50 | 5,09137 | (4,24793; 6,40914) |
| SuperPlant | 49 | 5,49969 | (4,48577; 7,08914) |
In diesen Ergebnissen geben die 95%-Bonferroni-Konfidenzintervalle an, dass Sie sich zu 95 % sicher sein können, dass die Gesamtheit der Konfidenzintervalle die tatsächlichen Standardabweichungen der Grundgesamtheiten für alle Gruppen enthält. Zudem zeigt das individuelle Konfidenzniveau an, mit welcher Sicherheit Sie behaupten können, dass ein individuelles Konfidenzintervall die Standardabweichung der Grundgesamtheit der betreffenden Gruppe enthält. Sie können sich beispielsweise zu 98,3333 % sicher sein, dass die Standardabweichung für die Grundgesamtheit GrowFast innerhalb des Konfidenzintervalls (3,43659; 5,61790) liegt.
Individuelles Konfidenzniveau
Das individuelle Konfidenzniveau ist der Prozentsatz der Fälle, in denen ein einzelnes Konfidenzintervall die tatsächliche Standardabweichung für diese spezifische Gruppe enthält, wenn Sie die Untersuchung mehrmals wiederholen.
Wenn Sie die Anzahl der Konfidenzintervalle in einem Satz von Konfidenzintervallen erhöhen, steigt die Wahrscheinlichkeit, dass mindestens ein Konfidenzintervall nicht die tatsächliche Standardabweichung enthält. Das simultane Konfidenzniveau gibt an, mit welcher Sicherheit Sie annehmen können, dass der komplette Satz von Konfidenzintervallen die tatsächlichen Standardabweichungen der Grundgesamtheiten für alle Gruppen enthält.
Interpretation
Methode
| Nullhypothese | Alle Varianzen sind gleich. |
|---|---|
| Alternativhypothese | Mindestens eine Varianz weicht ab. |
| Signifikanzniveau | α = 0,05 |
95%-Bonferroni-KIs für Standardabweichungen
| Dünger | N | StdAbw | KI |
|---|---|---|---|
| GrowFast | 50 | 4,28743 | (3,43659; 5,61790) |
| Keiner | 50 | 5,09137 | (4,24793; 6,40914) |
| SuperPlant | 49 | 5,49969 | (4,48577; 7,08914) |
Sie können sich zu 98,3333 % sicher sein, dass jedes individuelle Konfidenzintervall die Standardabweichung der Grundgesamtheit für die betreffende Gruppe enthält. Sie können sich beispielsweise zu 98,3333 % sicher sein, dass die Standardabweichung für die Grundgesamtheit GrowFast innerhalb des Konfidenzintervalls (3,43659; 5,61790) liegt. Da insgesamt jedoch drei Konfidenzintervalle vorliegen, können Sie nur mit einer Sicherheit von 95 % davon ausgehen, dass alle Intervalle die tatsächlichen Werte enthalten.
Tests
Welche Typen von Tests auf gleiche Varianzen von Minitab angezeigt werden, hängt davon ab, ob Sie die Option Test auf Grundlage der Normalverteilung verwenden im Unterdialogfeld Optionen ausgewählt haben, sowie von der Anzahl der Gruppen in den Daten.
Mehrfachvergleichsmethode und Levene-Methode
Wenn Sie die Option Test auf Grundlage der Normalverteilung verwenden nicht ausgewählt haben, zeigt Minitab Testergebnisse sowohl für die Mehrfachvergleichsmethode als auch für die Levene-Methode an. Für die meisten stetigen Verteilungen ergeben beide Methoden eine Wahrscheinlichkeit eines Fehlers 1. Art, die nahe am angegebenen Signifikanzniveau (als α oder Alpha bezeichnet) liegt. Die Mehrfachvergleichsmethode weist i. d. R. eine höhere Trennschärfe auf. Wenn der p-Wert für die Mehrfachvergleichsmethode signifikant ist, können Sie mit dem zusammenfassenden Diagramm spezifische Grundgesamtheiten identifizieren, die Standardabweichungen aufweisen, die sich voneinander unterscheiden.
- Jede der Stichproben enthält weniger als 20 Beobachtungen.
- Die Verteilung von einer oder mehreren Grundgesamtheiten ist extrem schief oder hat stärker besetzte Randbereiche. Im Vergleich zu einer Normalverteilung besitzt eine Verteilung mit stärker besetzten Randbereichen mehr Daten am unteren bzw. oberen Ende.
Wenn der p-Wert für den Mehrfachvergleichstest kleiner als das gewählte Signifikanzniveau ist, sind die Differenzen zwischen einigen der Standardabweichungen statistisch signifikant. Verwenden Sie die Mehrfachvergleichsintervalle, um zu ermitteln, welche Standardabweichungen sich signifikant voneinander unterscheiden. Wenn zwei Intervalle nicht überlappen, unterscheiden sich die entsprechenden Standardabweichungen (und Varianzen) signifikant.
Wenn kleine Stichproben aus sehr schiefen Verteilungen oder Verteilungen mit stärker besetzten Randbereichen vorliegen, kann die Wahrscheinlichkeit eines Fehlers 1. Art für die Mehrfachvergleichsmethode höher als α sein. Wenn Ihnen unter diesen Umständen die Levene-Methode einen kleineren p-Wert als die Mehrfachvergleichsmethode liefert, sollten Sie Ihre Schlussfolgerungen auf der Levene-Methode basieren.
F-Test und Bartlett-Test
Wenn Sie die Option Test auf Grundlage der Normalverteilung verwenden auswählen und über zwei Gruppen verfügen, führt Minitab den F-Test aus. Wenn mindestens drei Gruppen vorliegen, führt Minitab hingegen den Bartlett-Test aus.
Der F-Test und der Bartlett-Test sind nur für normalverteilte Daten genau. Jede Abweichung von einer Normalverteilung kann dazu führen, dass diese Tests zu ungenauen Ergebnissen führen. Wenn die Daten jedoch einer Normalverteilung entsprechen, bieten der F-Test und der Bartlett-Test i. d. R. eine höhere Trennschärfe als die Mehrfachvergleichsmethode oder die Levene-Methode.
Wenn der p-Wert für den Test kleiner als das Signifikanzniveau ist, sind die Differenzen zwischen einigen der Standardabweichungen statistisch signifikant.
Teststatistik
Hinweis
Beim Mehrfachvergleichstest wird keine Teststatistik verwendet.
Interpretation
Minitab verwendet die Teststatistik, um den p-Wert zu berechnen, anhand dessen Sie eine Entscheidung über die statistische Signifikanz der Differenzen zwischen den Standardabweichungen treffen. Der p-Wert ist ein Wahrscheinlichkeitsmaß für die Anzeichen gegen die Annahme der Nullhypothese. Geringere Wahrscheinlichkeiten liefern stärkere Anzeichen dafür, dass die Nullhypothese nicht zutrifft.
Eine ausreichend hohe Teststatistik gibt an, dass die Differenz zwischen einigen der Standardabweichungen statistisch signifikant ist.
Sie können anhand der Teststatistik bestimmen, ob die Nullhypothese verworfen werden soll. Häufiger wird jedoch der p-Wert verwendet, da er leichter zu interpretieren ist.
p-Wert
Der p-Wert ist ein Wahrscheinlichkeitsmaß für die Anzeichen gegen die Annahme der Nullhypothese. Geringere Wahrscheinlichkeiten liefern stärkere Anzeichen dafür, dass die Nullhypothese nicht zutrifft.
Interpretation
Verwenden Sie den p-Wert, um zu bestimmen, ob die Differenzen zwischen den Standardabweichungen statistisch signifikant sind. Minitab zeigt die Ergebnisse von einem oder zwei Tests an, mit denen die Gleichheit der Varianzen untersucht wird. Wenn zwei p-Werte vorliegen und diese einander widersprechen, lesen Sie den Abschnitt „Tests“.
Um zu bestimmen, ob mindestens eine der Differenzen zwischen den Standardabweichungen statistisch signifikant ist, vergleichen Sie den p-Wert mit dem Signifikanzniveau, um die Nullhypothese auszuwerten. Die Nullhypothese besagt, dass alle Gruppenmittelwerte gleich sind. In der Regel ist ein Signifikanzniveau (als α oder Alpha bezeichnet) von 0,05 gut geeignet. Ein Signifikanzniveau von 0,05 gibt ein Risiko von 5 % an, dass auf eine vorhandene Differenz geschlossen wird, während tatsächlich keine vorhanden ist.
- Wenn der p-Wert größer als α ist, sind die Differenzen zwischen den Standardabweichungen statistisch nicht signifikant.
- Wenn der p-Wert kleiner oder gleich α ist, sind die Differenzen zwischen einigen Standardabweichungen statistisch signifikant.
Zusammenfassendes Diagramm
Im zusammenfassenden Diagramm werden p-Werte und Konfidenzintervalle für die Tests auf gleiche Varianzen angezeigt. Welche Typen von Tests und Intervallen von Minitab angezeigt werden, hängt davon ab, ob Sie die Option Test auf Grundlage der Normalverteilung verwenden im Dialogfeld Optionen ausgewählt haben, sowie von der Anzahl der Gruppen in den Daten.
Wenn Sie die Option Test auf Grundlage der Normalverteilung verwenden nicht ausgewählt haben, werden im zusammenfassenden Diagramm p-Werte sowohl für die Mehrfachvergleichsmethode als auch für die Levene-Methode angezeigt. Im Diagramm werden zudem Mehrfachvergleichsintervalle abgebildet. Treffen Sie die Auswahl zwischen den Methoden auf der Grundlage der Eigenschaften Ihrer Daten.
Wenn Sie die Option Test auf Grundlage der Normalverteilung verwenden ausgewählt haben und über zwei Gruppen verfügen, führt Minitab den F-Test aus. Wenn mindestens drei Gruppen vorliegen, führt Minitab hingegen den Bartlett-Test aus. Für jeden dieser Tests werden im Diagramm außerdem Bonferroni-Konfidenzintervalle angezeigt.
p-Werte
Der p-Wert ist ein Wahrscheinlichkeitsmaß für die Anzeichen gegen die Annahme der Nullhypothese. Geringere Wahrscheinlichkeiten liefern stärkere Anzeichen dafür, dass die Nullhypothese nicht zutrifft.
Verwenden Sie die p-Werte, um zu bestimmen, ob die Differenzen zwischen den Standardabweichungen statistisch signifikant sind. Minitab zeigt die Ergebnisse von einem oder zwei Tests an, mit denen die Gleichheit der Varianzen untersucht wird. Wenn zwei p-Werte vorliegen und diese einander widersprechen, lesen Sie im Abschnitt zu den Tests nach, welcher Test verwendet werden sollte.
Um zu bestimmen, ob mindestens eine der Differenzen zwischen den Standardabweichungen statistisch signifikant ist, vergleichen Sie den p-Wert mit dem Signifikanzniveau, um die Nullhypothese auszuwerten. Die Nullhypothese besagt, dass alle Standardabweichungen der Gruppen gleich sind. In der Regel ist ein Signifikanzniveau (als α oder Alpha bezeichnet) von 0,05 gut geeignet. Ein Signifikanzniveau von 0,05 gibt ein Risiko von 5 % an, dass auf eine vorhandene Differenz geschlossen wird, während tatsächlich keine vorhanden ist.
- Wenn der p-Wert größer als α ist, sind die Differenzen zwischen den Standardabweichungen statistisch nicht signifikant.
- Wenn der p-Wert kleiner oder gleich α ist, sind die Differenzen zwischen einigen Standardabweichungen statistisch signifikant.
Intervalle für Mehrfachvergleiche
Wenn Sie die Option Test auf Grundlage der Normalverteilung verwenden nicht ausgewählt haben, werden im zusammenfassenden Diagramm Mehrfachvergleichsintervalle angezeigt.
Wenn Sie den p-Wert für Mehrfachvergleiche verwenden können, können Sie anhand der Konfidenzintervalle für die Mehrfachvergleiche die spezifischen Paare von Gruppen ermitteln, die eine statistisch signifikante Differenz aufweisen. Wenn zwei Intervalle nicht überlappen, ist die Differenz zwischen den entsprechenden Standardabweichungen statistisch signifikant.
Wenn die Eigenschaften der Daten die Verwendung der Levene-Methode erfordern, werten Sie die Konfidenzintervalle im zusammenfassenden Diagramm nicht aus.
Bonferroni-Konfidenzintervalle
Wenn Sie die Option Test auf Grundlage der Normalverteilung verwenden ausgewählt haben, werden im zusammenfassenden Diagramm Bonferroni-Konfidenzintervalle angezeigt.
Verwenden Sie die Bonferroni-Konfidenzintervalle, um die Standardabweichung jeder Grundgesamtheit für die kategorialen Faktoren zu schätzen. Jedes Konfidenzintervall ist ein Bereich von Werten, der wahrscheinlich die Standardabweichung der entsprechenden Grundgesamtheit enthält. Minitab korrigiert die Bonferroni-Konfidenzintervalle, um das simultane Konfidenzniveau beizubehalten.
Das Beibehalten des simultanen Konfidenzniveaus ist insbesondere dann wichtig, wenn mehrere Konfidenzintervalle untersucht werden. Wenn das simultane Konfidenzniveau nicht beibehalten wird, erhöht sich mit zunehmender Anzahl von Konfidenzintervallen die Wahrscheinlichkeit, dass mindestens ein Konfidenzintervall nicht die tatsächliche Standardabweichung enthält.
Weitere Informationen finden Sie unter Grundlagen von individuellen und simultanen Konfidenzniveaus in Mehrfachvergleichen und Was ist die Bonferroni-Methode?
Hinweis
Mit den Bonferroni-Konfidenzintervallen können Sie nicht ermitteln, ob die Differenzen zwischen Paaren von Gruppen statistisch signifikant sind. Verwenden Sie die p-Werte und die Konfidenzintervalle für Mehrfachvergleiche im zusammenfassenden Diagramm, um die statistische Signifikanz der Differenzen zu ermitteln.
Interpretation
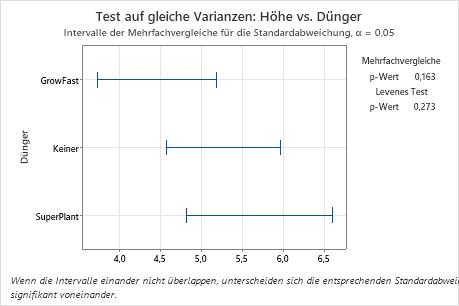
In diesem zusammenfassenden Diagramm ist der p-Wert für den Mehrfachvergleichstest größer als das Signifikanzniveau 0,05. Keine der Differenzen zwischen den Gruppen ist statistisch signifikant, und sämtliche Mehrfachvergleichsintervalle überlappen.
Einzelwertdiagramm
In einem Einzelwertdiagramm werden die Einzelwerte in jeder Stichprobe gezeigt. Mit einem Einzelwertdiagramm lassen sich die Stichproben leicht vergleichen. Jeder Kreis stellt eine Beobachtung dar. Die Verwendung eines Einzelwertdiagramms empfiehlt sich insbesondere bei kleinen Stichprobenumfängen.
Interpretation
Verwenden Sie ein Einzelwertdiagramm, um die Streubreite der Daten zu untersuchen und potenzielle Ausreißer zu identifizieren. Einzelwertdiagramme empfehlen sich insbesondere für Stichprobenumfänge kleiner als 50.
- Schiefe Daten
-
Untersuchen Sie die Streubreite der Daten, um zu ermitteln, ob die Daten schief sind. Wenn die Daten schief sind, liegen die meisten Datenwerte am oberen oder unteren Rand der Grafik. Schiefe Daten weisen darauf hin, dass die Daten möglicherweise nicht normalverteilt sind. Häufig lässt sich die Schiefe am einfachsten mit einem Einzelwertdiagramm, einem Histogramm oder einem Boxplot erkennen.
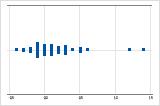
Rechtsschief

Linksschief
Das Einzelwertdiagramm mit rechtsschiefen Daten zeigt Wartezeiten. Der Großteil der Wartezeiten ist relativ kurz, und nur wenige Wartezeiten sind länger. Das Einzelwertdiagramm mit linksschiefen Daten zeigt Ausfallzeiten. Einige Elemente fallen sofort aus, deutlich mehr Elemente fallen später aus.
- Ausreißer
-
Ausreißer, d. h. Datenwerte, die weit entfernt von den anderen Datenwerten liegen, können sich stark auf Ihre Ergebnisse auswirken. Häufig lassen sich Ausreißer einfach in einem Einzelwertdiagramm erkennen.
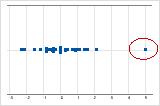
In einem Einzelwertdiagramm weisen ungewöhnlich hohe oder niedrige Datenwerte auf mögliche Ausreißer hin.
Versuchen Sie, die Ursache für die Ausreißer zu ermitteln. Korrigieren Sie sämtliche Dateneingabe- oder Messfehler. Erwägen Sie, Datenwerte zu entfernen, die auf ungewöhnliche, einmalige Ereignisse (Ausnahmebedingungen) zurückzuführen sind. Wiederholen Sie anschließend die Analyse.
Boxplot
Ein Boxplot ist eine grafische Zusammenfassung der Verteilung der einzelnen Stichproben. Mit dem Boxplot lassen sich die Form, Zentraltendenz und Streuung der Stichproben leicht vergleichen.
Interpretation
Verwenden Sie ein Boxplot, um die Streubreite der Daten zu untersuchen und um potenzielle Ausreißer zu identifizieren. Boxplots empfehlen sich insbesondere für Stichprobenumfänge größer als 20.
- Schiefe Daten
-
Untersuchen Sie die Streubreite der Daten, um zu ermitteln, ob die Daten schief sind. Wenn die Daten schief sind, liegen die meisten Datenwerte am oberen oder unteren Rand der Grafik. Schiefe Daten weisen darauf hin, dass die Daten möglicherweise nicht normalverteilt sind. Häufig lässt sich die Schiefe am einfachsten mit einem Einzelwertdiagramm, einem Histogramm oder einem Boxplot erkennen.
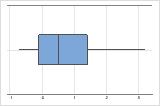
Rechtsschief
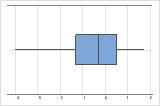
Linksschief
Das Boxplot mit rechtsschiefen Daten zeigt durchschnittliche Wartezeiten. Der Großteil der Wartezeiten ist relativ kurz, und nur wenige Wartezeiten sind länger. Das Boxplot mit linksschiefen Daten zeigt Ausfallraten. Einige Elemente fallen sofort aus, deutlich mehr Elemente fallen später aus.
Stark schiefe Daten können die Gültigkeit des p-Werts beeinträchtigen, wenn die Stichprobe klein ist (< 20 Werte). Wenn die Daten stark schief sind und eine kleine Stichprobe vorliegt, erwägen Sie, den Stichprobenumfang zu vergrößern.
- Ausreißer
-
Ausreißer, d. h. Datenwerte, die weit entfernt von den anderen Datenwerten liegen, können sich stark auf Ihre Ergebnisse auswirken. Häufig lassen sich Ausreißer am einfachsten in einem Boxplot erkennen.
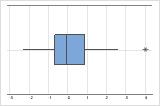
In einem Boxplot werden Ausreißer mit einem Sternchen (*) gekennzeichnet.
Versuchen Sie, die Ursache für die Ausreißer zu ermitteln. Korrigieren Sie sämtliche Dateneingabe- oder Messfehler. Erwägen Sie, Datenwerte zu entfernen, die auf ungewöhnliche, einmalige Ereignisse (Ausnahmebedingungen) zurückzuführen sind. Wiederholen Sie anschließend die Analyse.
