In diesem Thema
Bedingter angepasster Wert
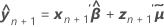
Notation
| Begriff | Beschreibung |
|---|---|
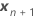 | Vektor der neuen Einstellungen für die Terme der festen Effekte |
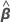 | geschätzte Koeffizienten für die Terme der festen Effekte |
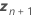 | Vektor der neuen Einstellungen für die Zufallsterme |
 | BLUP-Prognosen für die Zufallsterme |
Standardfehler des bedingten angepassten Werts (SE Anpassung)
Der Standardfehler eines bedingten angepassten Werts ist gleich der Quadratwurzel des folgenden Varianzausdrucks.
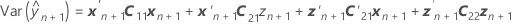
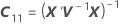
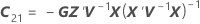

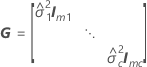
X ist die Designmatrix für die Terme der festen Effekte, und Z ist die Designmatrix für die Zufallsterme.
Konfidenzintervalle für bedingte Mittelwerte
Der Bereich, in dem der Mittelwert der Antwortvariablen bei einer gegebenen Gruppe von Werten der Prädiktorvariablen erwartet wird.

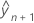 ist die bedingte Anpassung.
ist die bedingte Anpassung. 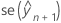 ist der Standardfehler der Anpassung.
ist der Standardfehler der Anpassung.
Bei den Freiheitsgraden wird diese Formel für den bedingten Fall verwendet:
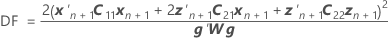
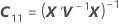
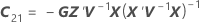

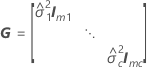
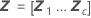
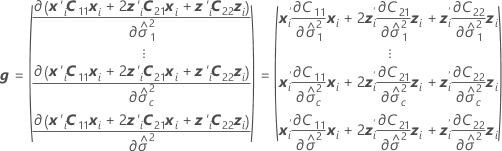



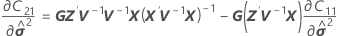
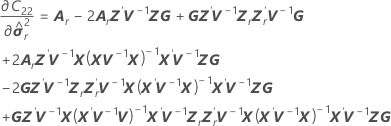
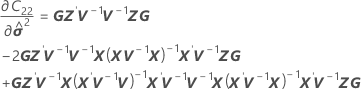
Notation
| Begriff | Beschreibung |
|---|---|
| W | die asymptotische Varianz-Kovarianz-Matrix von 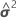 |
Weitere Informationen zur Notation finden Sie unter Bedingte Anpassungen und Residuen in „Modell mit gemischten Effekten anpassen“.
Bedingtes Prognoseintervall
Das bedingte Prognoseintervall lautet:

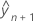 ist die bedingte Anpassung bei der neuen Variableneinstellung.
ist die bedingte Anpassung bei der neuen Variableneinstellung.
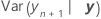 =
= 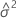
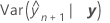 =
= 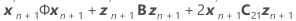
Bei den Freiheitsgraden wird diese Formel für den bedingten Fall verwendet:
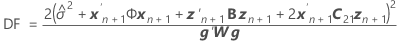
Dabei gilt Folgendes:
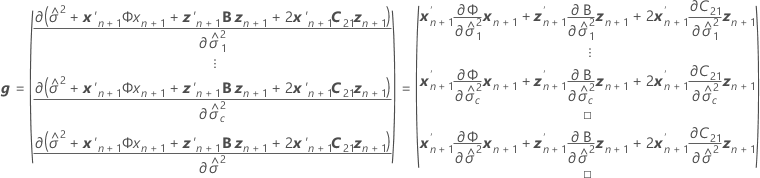
Notation
| Begriff | Beschreibung |
|---|---|
| W | asymptotische Varianz-Kovarianz-Matrix der Schätzwerte der Varianzkomponenten |
| I | Identitätsmatrix |
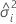 | Varianzkomponente für den i-ten Term mit Zufallseffekten |
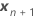 | Vektor der neuen Einstellungen für die Terme der festen Effekte |
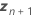 | Vektor der neuen Einstellungen für die Zufallsterme |
| c | Anzahl der Zufallsterme im Modell |
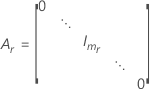
| B |
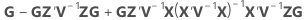 |
 |
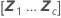 |
| C21 |
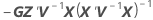 |
| G |
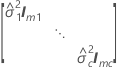 |
| mi | Anzahl der Stufen für den  Zufallseffekt Zufallseffekt |
| X | (n x p)-Designmatrix für die Terme der festen Effekte,  |
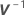 | Inverse der Varianz-Kovarianz-Matrix |
 | (n x mi)-Designmatrix für den  Zufallsterm im Modell Zufallsterm im Modell |
