Notation
| Begriff | Beschreibung |
|---|---|
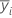 | Stichprobenmittelwert für die i-te Faktorstufe |
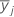 | Stichprobenmittelwert für die j-te Faktorstufe |
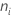 | Anzahl der Beobachtungen in Stufe i |
| r | Anzahl der Stufen |
| s | zusammengefasste Standardabweichung oder Quadratwurzel von MSE |
| u | Freiheitsgrade für Fehler |
| α | simultane Wahrscheinlichkeit eines Fehlers 1. Art |
| α* | individuelle Wahrscheinlichkeit eines Fehlers 1. Art |
Tukey:
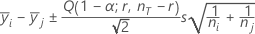
Hierbei ist Q = oberes α-Perzentil der Verteilung der studentisierten Spannweiten mit r und nT - r Freiheitsgraden.
Verwenden Sie die folgende Formel, um die individuelle Irrtumswahrscheinlichkeit anhand der simultanen Irrtumswahrscheinlichkeit zu ermitteln:

Fisher:
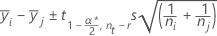
Hierbei ist t = oberer α/2-Punkt der Student-t-Verteilung mit u DF.
Verwenden Sie die folgende Formel, um das simultane Konfidenzniveau anhand der individuellen Irrtumswahrscheinlichkeit zu ermitteln:

Dunnett:

Die Berechnung von d wird in Hsu1 auf Seite 63 beschrieben.
Hsu-MCB:
An dieser Stelle werden Formeln für das Szenario aufgeführt, in dem alle Gruppengrößen gleich n sind. Formeln für ungleiche Gruppengrößen finden Sie in Hsu1. Angenommen, der größte Mittelwert sei der beste Mittelwert, und Sie möchten das Konfidenzintervall des i-ten Mittelwerts minus dem größten der verbleibenden ermitteln.
Der untere Endpunkt ist null oder, wenn kleiner, gleich

Der obere Endpunkt ist null oder, wenn größer, gleich

Die Berechnung von d wird in Hsu1 auf Seite 83 beschrieben.
Wenn der kleinste der Stufenmittelwerte als bester gewählt wurde, sind die Formeln identisch; das Maximum wird jedoch durch das Minimum ersetzt.
Games-Howell und Welch-Test
Die Welch-Teststatistik wird wie folgt berechnet.
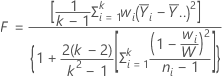
Der p-Wert für den Welch-Test ist eine Wahrscheinlichkeit für den oberen Randbereich einer F-Verteilung mit k – 1 Freiheitsgraden des Zählers, wobei k die Anzahl der X-Stufen ist und die Freiheitsgrade des Nenners wie folgt angegeben werden:
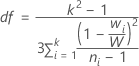
Das Vergleichsintervall für μi – μj ist
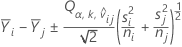
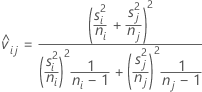
Das t-Verhältnis zum Berechnen des korrigierten p-Werts ist gleich:
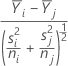
Dabei gilt Folgendes:
Der j-te Wert der Antwortvariablen in der i-ten Stufe des kategorialen Faktors ist gleich:Yij, j = 1, ... , ni; i = 1, ... k
Der durchschnittliche Wert der Antwortvariablen auf der i-ten Stufe ist gleich:
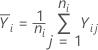
Die Stichprobenvarianz ist gleich:
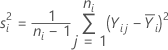
Die Gewichtung für Stufe i ist gleich:
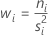
Die Summe aller Gewichtungen ist gleich:
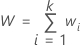
Der gewichtete Gesamtdurchschnitt der Antwortvariablen ist gleich:
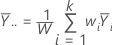
Danksagung
Unser herzlicher Dank für die Unterstützung beim Entwickeln und Implementieren von Mehrfachvergleichen geht an Jason C. Hsu.
[1] J.C. Hsu (1996). Multiple Comparisons, Theory and Methods. Chapman & Hall.
