In diesem Thema
Notation
Die Notation ist unerlässlich für das Verständnis von ANOVA-Modellen. Unten ist die Notation für eine einfache Varianzanalyse aufgeführt.
| Begriff | Beschreibung |
|---|---|
| r | Anzahl der Stufen des Faktors, i = 1 ...r |
| i | eine gegebene Faktorstufe |
| j | ein gegebener Fall für eine bestimmte Faktorstufe, j = 1 ...n i |
| yij | j-te Beobachtung der Antwortvariablen für die i-te Faktorstufe |
| ni | Anzahl der Beobachtungen für die i-te Faktorstufe |
| n T | Gesamtzahl der Fälle |
| μi | tatsächlicher Mittelwert der Beobachtungen auf der i-ten Faktorstufe |
| yi. | Summe der Beobachtungen auf der i-ten Faktorstufe |
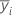 | Mittelwert der Antwortvariablen für den i-ten Faktor |
Modellanpassung
Formel
Es gibt verschiedene Möglichkeiten, das einfache Varianzanalysemodell anzugeben. Das Modell der Zellenmittelwerte wird wie folgt ausgedrückt:
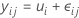
Für alle Beobachtungen für die Faktorstufe gilt dieselbe Erwartung, μ i . Da μi eine Konstante darstellt, weisen alle Beobachtungen ungeachtet der Faktorstufe dieselbe Varianz auf.
Bei der Varianzanalyse wird die Schätzmethode der kleinsten Quadrate verwendet, um das Modell anzupassen und Schätzwerte für die Parameter μi zu berechnen.
Der Hypothesentest für die einfache Varianzanalyse wird wie folgt ausgedrückt:
H0: μ 1 = μ 2= … = μ r
H1: Mindestens ein Mittelwert ist nicht gleich den anderen Mittelwerten.
Notation
| Begriff | Beschreibung |
|---|---|
| μ i | Parameter oder der tatsächliche Mittelwert der Beobachtungen auf der i-ten Faktorstufe |
| ε ij | Fehler, der unabhängig und normalverteilt ist und den Mittelwert 0 sowie die konstante Varianz σ 2 aufweist |
