Methoden und Formeln für die Varianzanalyse in Einfache ANOVA

Wählen Sie die gewünschte Methode oder Formel aus.

In diesem Thema

Freiheitsgrade (DF)
Summe der Quadrate (SS)
Mittel der Quadrate (MS)
F-Wert
p-Wert
S
R-Qd
R-Qd(kor)
R-Qd (prog)

Freiheitsgrade (DF)

Formel

Gibt die Anzahl der unabhängigen Elemente in der Summe der Quadrate an. Die Freiheitsgrade für jede Komponente des Modells werden wie folgt ausgedrückt:

DF (Faktor) = r – 1
DF Fehler = n_T – r
Gesamt = n_T – 1

Notation

Begriff	Beschreibung
n_T	Gesamtzahl der Beobachtungen
r	Anzahl der Faktorstufen

Summe der Quadrate (SS)

Formel

Die Summe der quadrierten Distanzen. SS Gesamt gibt die Gesamtstreuung der Daten an. SS (Faktor) ist die Abweichung des geschätzten Mittelwerts der Faktorstufe vom Gesamtmittelwert. Gelegentlich wird dies auch als Summe der Quadrate zwischen Behandlungen bezeichnet. SS Fehler ist die Abweichung einer Beobachtung von ihrem entsprechenden Mittelwert der Faktorstufe. Dies wird auch als Fehler innerhalb von Behandlungen bezeichnet.

Die Berechnungen lauten wie folgt:

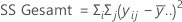
Notation

Begriff	Beschreibung
y̅_i _.	Mittelwert der Beobachtungen auf der i-ten Faktorstufe
y̅..	Mittelwert aller Beobachtungen
y_ij	Wert der j-ten Beobachtung auf der i-ten Faktorstufe

Mittel der Quadrate (MS)

Formel

Das Mittel der Quadrate für den Faktor wird wie folgt berechnet:

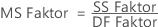
Das Mittel der Quadrate für den Fehler wird wie folgt berechnet:

Notation

Begriff	Beschreibung
MS	Mittel der Quadrate
SS	Summe der Quadrate
DF	Freiheitsgrade

F-Wert

Formel

Die Freiheitsgrade für den Zähler sind r – 1. Die Freiheitsgrade für den Nenner sind n_T – r.

Notation

Begriff	Beschreibung
n_T	Gesamtzahl der Beobachtungen
r	Anzahl der Faktorstufen

p-Wert

Werden in Hypothesentests verwendet, um Ihnen die Entscheidung zu ermöglichen, ob eine Nullhypothese zurückgewiesen oder nicht zurückgewiesen werden sollte. Der p-Wert stellt die Wahrscheinlichkeit dar, eine Teststatistik zu erhalten, die mindestens so extrem wie der tatsächlich berechnete Wert ist, wenn die Nullhypothese wahr ist. Ein häufig verwendeter Trennwert für den p-Wert ist 0,05. Wenn der berechnete p-Wert einer Teststatistik beispielsweise kleiner als 0,05 ist, weisen Sie die Nullhypothese zurück.

S

Ein Schätzwert von σ, das Maß der Standardabweichung innerhalb der Stichprobe. Beachten Sie, dass S² = MS Fehler. Dies entspricht der zusammengefassten Standardabweichung, mit der die individuellen Konfidenzintervalle berechnet werden.

R-Qd

Die Formel kann auch wie folgt ausgedrückt werden:

R² kann auch berechnet werden als quadrierte Korrelation von y und .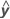

Notation

Begriff	Beschreibung
SS	Summe der Quadrate
y	Antwortvariable
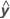	angepasste Antwortvariable

R-Qd(kor)

Notation

Begriff	Beschreibung
MS	Mittel der Quadrate
SS	Summe der Quadrate
DF	Freiheitsgrade

R-Qd (prog)

Obwohl die Berechnungen für R² (prog) negative Werte ergeben können, zeigt Minitab in derartigen Fällen null an.

Notation

Begriff	Beschreibung
y_i	i-ter beobachteter Wert der Antwortvariablen
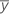	Mittelwert der Antwortvariablen
n	Anzahl der Beobachtungen
e_i	i-tes Residuum
h_i	i-tes Diagonalelement von X(X'X)^–1X'
X	Designmatrix