In diesem Thema
- Schritt 1: Bestimmen, ob die Differenzen zwischen den Mittelwerten der Gruppen statistisch signifikant sind
- Schritt 2: Untersuchen der Gruppenmittelwerte
- Schritt 3: Vergleichen der Gruppenmittelwerte
- Schritt 4: Bestimmen, wie gut das Modell an die Daten angepasst ist
- Schritt 5: Bestimmen, ob das Modell die Annahmen der Analyse erfüllt
Schritt 1: Bestimmen, ob die Differenzen zwischen den Mittelwerten der Gruppen statistisch signifikant sind
- p-Wert ≤ α: Die Differenzen zwischen einigen der Mittelwerte sind statistisch signifikant
- Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, weisen Sie die Nullhypothese zurück und schlussfolgern, dass nicht alle Mittelwerte der Grundgesamtheiten gleich sind. Bestimmen Sie anhand Ihres Fachwissens, ob die Differenzen praktisch signifikant sind. Weitere Informationen finden Sie unter Statistische und praktische Signifikanz.
- p-Wert > α: Die Differenzen zwischen den Mittelwerten sind statistisch nicht signifikant
- Wenn der p-Wert größer als das Signifikanzniveau ist, liegen keine ausreichenden Anzeichen zum Zurückweisen der Nullhypothese vor, die besagt, dass alle Mittelwerte der Grundgesamtheiten gleich sind. Vergewissern Sie sich, dass der Test über eine ausreichende Trennschärfe verfügt, um eine praktisch signifikante Differenz zu erkennen. Weitere Informationen finden Sie unter Steigern der Trennschärfe eines Hypothesentests.
Varianzanalyse
| Quelle | DF | Kor SS | Kor MS | F-Wert | p-Wert |
|---|---|---|---|---|---|
| Lack | 3 | 281,7 | 93,90 | 6,02 | 0,004 |
| Fehler | 20 | 312,1 | 15,60 | ||
| Gesamt | 23 | 593,8 |
Wichtigstes Ergebnis: p-Wert
In diesen Ergebnissen besagt die Nullhypothese, dass die Werte der mittleren Härte für vier verschiedene Lacke gleich sind. Da der p-Wert kleiner als das Signifikanzniveau 0,05 ist, können Sie die Nullhypothese zurückweisen und schlussfolgern, dass einige Lacke abweichende Mittelwerte aufweisen.
Schritt 2: Untersuchen der Gruppenmittelwerte
Verwenden Sie das Fehlerbalkendiagramm, um den Mittelwert und das Konfidenzintervall für jede Gruppe anzuzeigen.
- Jeder Punkt stellt einen Stichprobenmittelwert dar.
- Jedes Intervall ist ein 95%-Konfidenzintervall für den Mittelwert einer Gruppe. Sie können sich zu 95 % sicher sein, dass ein Gruppenmittelwert im Konfidenzintervall der Gruppe enthalten ist.
Wichtig
Interpretieren Sie diese Intervalle mit Vorsicht, da beim Ausführen von Mehrfachvergleichen die Wahrscheinlichkeit eines Fehlers 1. Art ansteigt. Das heißt, mit zunehmender Anzahl der Vergleiche steigt auch die Wahrscheinlichkeit, dass bei mindestens einem Vergleich fälschlicherweise geschlussfolgert wird, dass eine der beobachteten Differenzen signifikant abweicht.
Um die in diesem Diagramm veranschaulichten Differenzen zu beurteilen, verwenden Sie die Tabelle der Gruppierungsinformationen sowie die weiteren Ausgaben der Vergleiche (erläutert in Schritt 3).
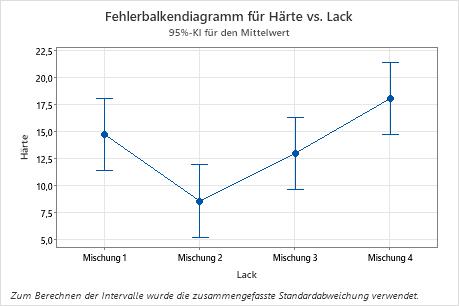
Im Fehlerbalkendiagramm weist Mischung 2 den niedrigsten und Mischung 4 den höchsten Mittelwert auf. Sie können anhand dieser Grafik nicht ermitteln, ob Differenzen statistisch signifikant sind. Um die statistische Signifikanz zu bestimmen, untersuchen Sie die Konfidenzintervalle für die Differenzen der Mittelwerte.
Schritt 3: Vergleichen der Gruppenmittelwerte
Wenn der p-Wert aus der einfachen ANOVA kleiner als das Signifikanzniveau ist, wissen Sie, dass einige der Gruppenmittelwerte abweichen, nicht jedoch, um welche Paare von Gruppen es sich handelt. Verwenden Sie die Tabelle der Gruppierungsinformationen und die Tests für Differenzen der Mittelwerte, um zu bestimmen, ob die Mittelwertdifferenz zwischen spezifischen Paaren von Gruppen statistisch signifikant ist, und um zu schätzen, um welchen Betrag sie voneinander abweichen.
Weitere Informationen zu Vergleichsmethoden finden Sie unter Verwenden von Mehrfachvergleichen zum Beurteilen der praktischen und statistischen Signifikanz.
- Tabelle „Gruppierungsinformationen“
-
Verwenden Sie die Tabelle „Gruppierungsinformationen“, um rasch zu ermitteln, ob die Mittelwertdifferenz zwischen einem beliebigen Paar von Gruppen statistisch signifikant ist.
Gruppen, die keinen Buchstaben teilen, sind signifikant unterschiedlich.
- Tests für Differenzen der Mittelwerte
-
Verwenden Sie die Konfidenzintervalle, um wahrscheinliche Bereiche für die Differenzen zu ermitteln und zu bestimmen, ob die Differenzen praktisch signifikant sind. Die Tabelle zeigt eine Gruppe von Konfidenzintervallen für die Differenzen zwischen Paaren von Mittelwerten. Das Fehlerbalkendiagramm für die Differenzen der Mittelwerte stellt dieselben Informationen dar.
Konfidenzintervalle, die den Wert null nicht enthalten, weisen auf eine statistisch signifikante Mittelwertdifferenz hin.
Je nach gewählter Vergleichsmethode werden in der Tabelle unterschiedliche Paare von Gruppen verglichen, und es wird einer der folgenden Typen von Konfidenzintervallen angezeigt.-
Individuelles Konfidenzniveau
Der Prozentsatz der Fälle, in denen ein einziges Konfidenzintervall die tatsächliche Differenz zwischen einem Paar von Gruppenmittelwerten enthält, wenn die Untersuchung mehrmals wiederholt wird.
-
Simultanes Konfidenzniveau
Der Prozentsatz der Fälle, in denen eine Gruppe von Konfidenzintervallen die tatsächlichen Differenzen für alle Gruppenvergleiche umfasst, wenn die Untersuchung mehrmals wiederholt wird.
Insbesondere bei mehreren Vergleichen ist es wichtig, das simultane Konfidenzniveau unter Kontrolle zu halten. Wenn das simultane Konfidenzniveau nicht unter Kontrolle ist, nimmt mit der Anzahl der Vergleiche die Wahrscheinlichkeit zu, das mindestens ein Konfidenzintervall nicht die tatsächliche Differenz enthält.
-
Weitere Informationen finden Sie unter Grundlagen von individuellen und simultanen Konfidenzniveaus in Mehrfachvergleichen.
Weitere Informationen zum Interpretieren der Ergebnisse der Hsu-MCB-Methode finden Sie unter Was sind Hsu-Mehrfachvergleiche mit dem Besten (MCB)?
Gruppierungsinformationen anhand der Tukey-Methode und 95%-Konfidenz
| Lack | N | Mittelwert | Gruppierung | |
|---|---|---|---|---|
| Mischung 4 | 6 | 18,07 | A | |
| Mischung 1 | 6 | 14,73 | A | B |
| Mischung 3 | 6 | 12,98 | A | B |
| Mischung 2 | 6 | 8,57 | B | |
Wichtigste Ergebnisse: Mittelwert, Gruppierung
In diesen Ergebnissen wird in der Tabelle ersichtlich, dass Gruppe A die Mischungen 1, 3 und 4 enthält, während Gruppe B die Mischungen 1, 2 und 3 enthält. Die Mischungen 1 und 3 sind in beiden Gruppen vorhanden. Differenzen zwischen Mittelwerten, die einen gemeinsamen Buchstaben aufweisen, sind statistisch nicht signifikant. Die Mischungen 2 und 4 weisen keinen gemeinsamen Buchstaben auf, und dies weist darauf hin, dass der Mittelwert von Mischung 4 signifikant größer als der von Mischung 2 ist.
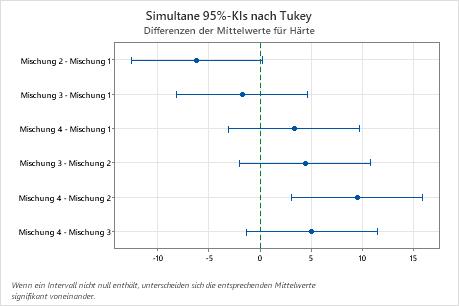
Simultane Tukey-Tests für Differenzen der Mittelwerte
| Differenz der Stufen | Differenz der Mittelwerte | SE der Differenz | 95%-KI | t-Wert | Korrigierter p-Wert |
|---|---|---|---|---|---|
| Mischung 2 - Mischung 1 | -6,17 | 2,28 | (-12,55; 0,22) | -2,70 | 0,061 |
| Mischung 3 - Mischung 1 | -1,75 | 2,28 | (-8,14; 4,64) | -0,77 | 0,868 |
| Mischung 4 - Mischung 1 | 3,33 | 2,28 | (-3,05; 9,72) | 1,46 | 0,478 |
| Mischung 3 - Mischung 2 | 4,42 | 2,28 | (-1,97; 10,80) | 1,94 | 0,245 |
| Mischung 4 - Mischung 2 | 9,50 | 2,28 | (3,11; 15,89) | 4,17 | 0,002 |
| Mischung 4 - Mischung 3 | 5,08 | 2,28 | (-1,30; 11,47) | 2,23 | 0,150 |
Wichtigste Ergebnisse: Simultane 95%-KIs, individuelles Konfidenzniveau
- Das Konfidenzintervall für die Differenz zwischen den Mittelwerten von Mischung 2 und Mischung 4 erstreckt sich von 3,11 bis 15,89. Dieser Bereich enthält nicht den Wert null, was darauf hinweist, dass die Differenz statistisch signifikant ist.
- Die Konfidenzintervalle für alle weiteren Mittelwertpaare enthalten den Wert null, was darauf hinweist, dass die Differenzen statistisch nicht signifikant sind.
- Das simultane 95%-Konfidenzniveau gibt an, dass Sie sich zu 95 % sicher sein können, dass alle Konfidenzintervalle die tatsächlichen Differenzen enthalten.
- Die Tabelle gibt an, dass das individuelle Konfidenzniveau 98,89 % beträgt. Dieses Ergebnis deutet darauf hin, dass Sie sich zu 98,89 % sicher sein können, dass jedes individuelle Intervall die tatsächliche Differenz zwischen einem spezifischen Paar von Gruppenmittelwerten enthält. Die individuellen Konfidenzniveaus für die einzelnen Vergleiche erzeugen das simultane 95%-Konfidenzniveau für alle sechs Vergleiche.
Schritt 4: Bestimmen, wie gut das Modell an die Daten angepasst ist
Um zu ermitteln, wie gut das Modell an die Daten angepasst ist, untersuchen Sie die Statistiken für die Güte der Anpassung in der Tabelle „Zusammenfassung des Modells“.
- S
- Verwenden Sie S, um zu ermitteln, wie genau das Modell die Antwortvariable beschreibt.
S wird in der Maßeinheit der Antwortvariablen ausgedrückt und stellt den Abstand der Datenwerte von den angepassten Werten dar. Je niedriger der Wert von S, desto genauer beschreibt das Modell die Antwortvariable. Ein niedriger Wert von S allein bedeutet jedoch nicht zwangsläufig, dass das Modell die Modellannahmen erfüllt. Prüfen Sie die Annahmen anhand der Residuendiagramme.
- R-Qd
-
R2 gibt den Prozentsatz der Streuung der Antwortvariablen an, der durch das Modell erklärt wird. Je höher das R2, desto besser ist das Modell an die Daten angepasst. Das R2 liegt immer zwischen 0 % und 100 %.
Ein hoher Wert von R2 bedeutet nicht zwangsläufig, dass das Modell die Modellannahmen erfüllt. Prüfen Sie die Annahmen anhand der Residuendiagramme.
- R-Qd (prog)
-
Verwenden Sie das prognostizierte R2, um zu ermitteln, wie genau das Modell Werte der Antwortvariablen für neue Beobachtungen prognostiziert. Modelle mit einem höheren prognostizierten R2 zeichnen sich durch eine bessere Prognosefähigkeit aus.
Ein prognostiziertes R2, das wesentlich kleiner als R2 ist, kann auf eine übermäßige Anpassung des Modells hinweisen. Ein übermäßig angepasstes Modell liegt vor, wenn Sie Terme für Effekte hinzufügen, die in der Grundgesamtheit unbedeutend sind. Das Modell wird somit an die Stichprobendaten angepasst und ist daher möglicherweise beim Aufstellen von Prognosen für die Grundgesamtheit nicht nützlich.
Das prognostizierte R2 kann zudem beim Vergleichen von Modellen nützlicher als das korrigierte R2 sein, da der Wert mit Beobachtungen berechnet wird, die in der Modellberechnung nicht enthalten sind.
Zusammenfassung des Modells
| S | R-Qd | R-Qd(kor) | R-Qd(prog) |
|---|---|---|---|
| 3,95012 | 47,44% | 39,56% | 24,32% |
Wichtigste Ergebnisse: S, R-Qd, R-Qd (prog)
In diesen Ergebnissen erklärt der Faktor 47,44 % der Streuung in der Antwortvariablen. S gibt an, dass die Standardabweichung zwischen den Datenpunkten und den angepassten Werten ca. 3,95 Einheiten beträgt.
Schritt 5: Bestimmen, ob das Modell die Annahmen der Analyse erfüllt
Verwenden Sie die Residuendiagramme, um zu ermitteln, ob das Modell angemessen ist und die Annahmen der Analyse erfüllt. Wenn die Annahmen nicht erfüllt werden, ist das Modell u. U. nicht gut an die Daten angepasst, und Sie sollten beim Interpretieren der Ergebnisse vorsichtig sein.
Diagramm der Residuen im Vergleich zu den Anpassungen
Verwenden Sie das Diagramm der Residuen im Vergleich zu den Anpassungen, um die Annahme zu überprüfen, dass die Residuen zufällig verteilt sind und eine konstante Varianz aufweisen. Im Idealfall sollten die Punkte zufällig auf beiden Seiten von null verteilt sein, und es sollten keine Muster in den Punkten erkennbar sein.
| Muster | Mögliche Bedeutung des Musters |
|---|---|
| Aufgefächerte oder ungleichmäßig gestreute Residuen für die angepassten Werte | Nicht konstante Varianz |
| Ein weit von null entfernt liegender Punkt | Ein Ausreißer |
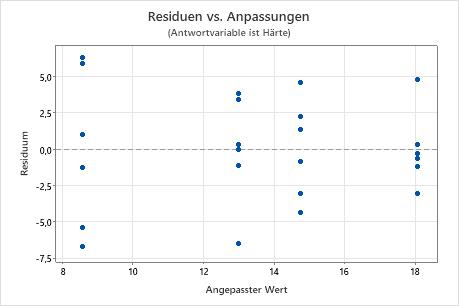
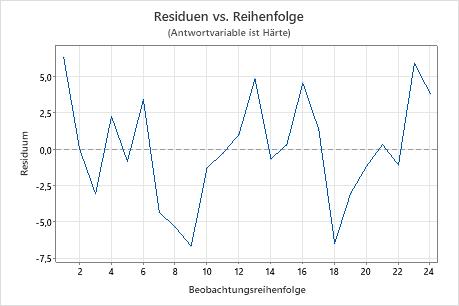
Diagramm der Residuen im Vergleich zur Reihenfolge
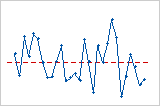
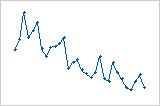
Trend
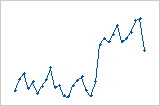
Shift
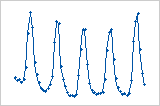
Zyklus
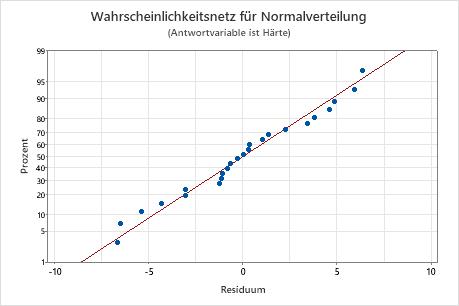
Wahrscheinlichkeitsnetz (Normal) für Residuen
Verwenden Sie das Wahrscheinlichkeitsnetz (Normal) der Residuen, um die Annahme zu überprüfen, dass die Residuen normalverteilt sind. Die Residuen im Wahrscheinlichkeitsnetz für Normalverteilung sollten ungefähr einer Geraden folgen.
| Muster | Mögliche Bedeutung des Musters |
|---|---|
| Keine Gerade | Nicht-Normalverteilung |
| Ein Punkt weit entfernt von der Linie | Ein Ausreißer |
| Unbeständige Steigung | Eine nicht identifizierte Variable |
Hinweis
Wenn das Design der einfachen ANOVA den Richtlinien für den Stichprobenumfang entspricht, werden die Ergebnisse durch Abweichungen von der Normalverteilung nicht wesentlich beeinträchtigt.