In diesem Thema
N
Der Stichprobenumfang (N) gibt die Gesamtzahl der Beobachtungen in jeder Gruppe an.
Interpretation
Der Stichprobenumfang wirkt sich auf das Konfidenzintervall und auf die Trennschärfe des Tests aus.
Eine größere Stichprobe führt in der Regel zu einem schmaleren Konfidenzintervall. Bei größeren Stichprobenumfängen verfügt der Test außerdem über eine höhere Trennschärfe zum Erkennen einer Differenz.
Mittelwert
Der Mittelwert der Beobachtungen in jeder Gruppe. Der Mittelwert beschreibt jede Gruppe mit einem einzelnen Wert, der das Zentrum der Daten darstellt. Dabei handelt es sich um die Summe aller Beobachtungen in einer Gruppe dividiert durch die Anzahl der Beobachtungen in der betreffenden Gruppe.
Interpretation
Der Mittelwert jeder Stichprobe ist ein Schätzwert für den Mittelwert der Grundgesamtheit. Die Differenzen zwischen den Stichprobenmittelwerten sind Schätzwerte der Differenzen zwischen den Mittelwerten der Grundgesamtheiten.
Da die Differenz zwischen zwei Gruppenmittelwerten auf Daten aus einer Stichprobe und nicht auf den Daten der vollständigen Grundgesamtheit basiert, können Sie sich nicht sicher sein, dass sie gleich der Differenz der Grundgesamtheit ist. Verwenden Sie das Konfidenzintervall, um die Differenz der Grundgesamtheit besser einschätzen zu können.
Gruppierung
Verwenden Sie die Tabelle der Gruppierungsinformationen, um rasch zu ermitteln, ob die Mittelwertdifferenz zwischen einem beliebigen Paar von Gruppen statistisch signifikant ist.
Die Spalte „Gruppierung“ enthält Buchstaben, mit denen die Faktorstufen gruppiert werden. Gruppen, die keinen Buchstaben gemeinsam haben, weisen eine statistisch signifikante Mittelwertdifferenz auf.
Wenn in der Tabelle Differenzen aufgeführt werden, die statistisch signifikant sind, verwenden Sie die Konfidenzintervalle der Differenzen, um zu beurteilen, ob die Differenzen auch praktisch signifikant sind.
Interpretation
Gruppierungsinformationen anhand der Tukey-Methode und 95%-Konfidenz
| Lack | N | Mittelwert | Gruppierung | |
|---|---|---|---|---|
| Mischung 4 | 6 | 18,07 | A | |
| Mischung 1 | 6 | 14,73 | A | B |
| Mischung 3 | 6 | 12,98 | A | B |
| Mischung 2 | 6 | 8,57 | B | |
In diesen Ergebnissen wird in der Tabelle ersichtlich, dass Gruppe A die Mischungen 1, 3 und 4 enthält, während Gruppe B die Mischungen 1, 2 und 3 enthält. Die Mischungen 1 und 3 sind in beiden Gruppen vorhanden. Differenzen zwischen Mittelwerten, die einen gemeinsamen Buchstaben aufweisen, sind statistisch nicht signifikant. Die Mischungen 2 und 4 weisen keinen gemeinsamen Buchstaben auf, und dies weist darauf hin, dass der Mittelwert von Mischung 4 signifikant größer als der von Mischung 2 ist.
Individuelle Fisher-Tests für Differenzen der Mittelwerte
Verwenden Sie die individuellen Konfidenzintervalle, um statisch signifikante Differenzen zwischen den Gruppenmittelwerten zu ermitteln, wahrscheinliche Bereiche für die Differenzen zu bestimmen und festzustellen, ob die Differenzen statistisch signifikant sind. In der Tabelle für individuelle Tests nach Fisher wird eine Gruppe von Konfidenzintervallen für die Differenzen zwischen Paaren von Mittelwerten gezeigt.
Das individuelle Konfidenzniveau ist der Prozentsatz der Fälle, in denen ein einziges Konfidenzintervall die tatsächliche Differenz zwischen einem Paar von Gruppenmittelwerten enthält, wenn Sie die Untersuchung wiederholen. Individuelle Konfidenzintervalle sind nur für die Fisher-Methode verfügbar. Bei allen anderen Vergleichsmethoden werden simultane Konfidenzintervalle erzeugt.
Es ist unüblich, das individuelle Konfidenzniveau unter Kontrolle zu halten, da dabei nicht das simultane Konfidenzniveau unter Kontrolle gehalten wird, das in der Folge häufig auf inakzeptabel hohe Werte ansteigt. Wenn das simultane Konfidenzniveau nicht unter Kontrolle ist, nimmt mit der Anzahl der Vergleiche die Wahrscheinlichkeit zu, das mindestens ein Konfidenzintervall nicht die tatsächliche Differenz enthält.
Das Konfidenzintervall der Differenz setzt sich aus den folgenden zwei Teilen zusammen:
- Punktschätzung
- Die Punktschätzung ist die Differenz zwischen einem Paar von Mittelwerten; sie wird anhand der Stichprobendaten berechnet. Das Konfidenzintervall wird auf diesen Wert zentriert.
- Fehlerspanne
- Die Fehlerspanne definiert die Breite des Konfidenzintervalls, und sie wird durch die beobachtete Streuung in der Stichprobe und das Konfidenzniveau bestimmt. Zum Berechnen der Obergrenze des Konfidenzintervalls wird die Fehlerspanne zur Punktschätzung addiert. Zum Berechnen der Untergrenze des Konfidenzintervalls wird die Fehlerspanne von der Punktschätzung subtrahiert.
Interpretation
Verwenden Sie die Konfidenzintervalle, um die Differenzen zwischen den Gruppenmittelwerten auszuwerten.
Individuelle Fisher-Tests für Differenzen der Mittelwerte
| Differenz der Stufen | Differenz der Mittelwerte | SE der Differenz | 95%-KI | t-Wert | Korrigierter p-Wert |
|---|---|---|---|---|---|
| Mischung 2 - Mischung 1 | -6,17 | 2,28 | (-10,92; -1,41) | -2,70 | 0,014 |
| Mischung 3 - Mischung 1 | -1,75 | 2,28 | (-6,51; 3,01) | -0,77 | 0,452 |
| Mischung 4 - Mischung 1 | 3,33 | 2,28 | (-1,42; 8,09) | 1,46 | 0,159 |
| Mischung 3 - Mischung 2 | 4,42 | 2,28 | (-0,34; 9,17) | 1,94 | 0,067 |
| Mischung 4 - Mischung 2 | 9,50 | 2,28 | (4,74; 14,26) | 4,17 | 0,000 |
| Mischung 4 - Mischung 3 | 5,08 | 2,28 | (0,33; 9,84) | 2,23 | 0,037 |
- Das Konfidenzintervall für die Differenz zwischen den Mittelwerten von Mischung 4 und Mischung 2 erstreckt sich von 4,74 bis 14,26. Dieser Bereich enthält nicht den Wert null, was darauf hinweist, dass die Differenz zwischen diesen Mittelwerten statistisch signifikant ist.
- Das Konfidenzintervall für die Differenz zwischen den Mittelwerten von Mischung 2 und Mischung 1 erstreckt sich von -10,92 bis -1,41. Dieser Bereich enthält nicht den Wert null, was darauf hinweist, dass die Differenz zwischen diesen Mittelwerten statistisch signifikant ist.
- Das Konfidenzintervall für die Differenz zwischen den Mittelwerten von Mischung 4 und Mischung 3 erstreckt sich von 0,33 bis 9,84. Dieser Bereich enthält nicht den Wert null, was darauf hinweist, dass die Differenz zwischen diesen Mittelwerten statistisch signifikant ist.
- Die Konfidenzintervalle für alle weiteren Mittelwertpaare enthalten den Wert null, was darauf hinweist, dass die Differenzen statistisch nicht signifikant sind.
- Das individuelle 95%-Konfidenzniveau gibt an, dass Sie sich zu 95 % sicher sein können, dass jedes Konfidenzintervall die tatsächliche Differenz für den betreffenden Vergleich enthält. Das simultane Konfidenzniveau gibt hingegen an, dass Sie sich nur zu 80,83 % sicher sein können, dass sämtliche Intervalle die tatsächlichen Differenzen enthalten.
Differenz der Mittelwerte
Dieser Wert gibt die Differenz zwischen den Stichprobenmittelwerten von zwei Gruppen an.
Interpretation
Die Differenzen zwischen den Stichprobenmittelwerten der Gruppen sind Schätzwerte der Differenzen zwischen den Grundgesamtheiten dieser Gruppen.
Da jede Mittelwertdifferenz auf Daten aus einer Stichprobe und nicht auf den Daten der vollständigen Grundgesamtheit basiert, können Sie sich nicht sicher sein, dass sie gleich der Differenz der Grundgesamtheit ist. Verwenden Sie die Konfidenzintervalle, um die Differenzen zwischen den Mittelwerten der Grundgesamtheiten besser einschätzen zu können.
SE der Differenz
Mit dem Standardfehler der Differenz zwischen Mittelwerten (SE der Differenz) wird die Streuung der Differenz zwischen Stichprobenmittelwerten geschätzt, die Sie erhalten würden, wenn Sie wiederholt Stichproben aus denselben Grundgesamtheiten ziehen würden.
Interpretation
Verwenden Sie den Standardfehler der Differenz zwischen Mittelwerten, um zu ermitteln, wie präzise die Differenzen zwischen den Stichprobenmittelwerten die Differenzen zwischen den Mittelwerten der Grundgesamtheiten schätzen. Ein niedrigerer Wert des Standardfehlers verweist auf einen präziseren Schätzwert.
Minitab verwendet den Standardfehler der Differenz, um die Konfidenzintervalle der Differenzen zwischen Mittelwerten zu berechnen. Hierbei handelt es sich um einen Bereich von Werten, der wahrscheinlich die Differenzen der Grundgesamtheiten enthält.
95%-KI
Verwenden Sie die simultanen Konfidenzintervalle der Differenz (95%-KI), um statistisch signifikante Mittelwertdifferenzen zu identifizieren, wahrscheinliche Bereiche für die Differenzen zu bestimmen und die praktische Signifikanz der Differenzen zu beurteilen. Die Tabelle zeigt eine Gruppe von Konfidenzintervallen für die Differenzen zwischen Paaren von Mittelwerten. Konfidenzintervalle, die den Wert null nicht enthalten, weisen auf eine statistisch signifikante Mittelwertdifferenz hin.
Das simultane Konfidenzniveau gibt den Prozentsatz der Fälle an, in denen eine Gruppe von Konfidenzintervallen die tatsächlichen Differenzen für alle Gruppenvergleiche enthält, wenn Sie die Untersuchung mehrmals wiederholen würden.
Insbesondere bei mehreren Vergleichen ist es wichtig, das simultane Konfidenzniveau unter Kontrolle zu halten. Wenn das simultane Konfidenzniveau nicht unter Kontrolle ist, nimmt mit der Anzahl der Vergleiche die Wahrscheinlichkeit zu, das mindestens ein Konfidenzintervall nicht die tatsächliche Differenz enthält.
Das Konfidenzintervall der Differenz setzt sich aus den folgenden zwei Teilen zusammen:
- Punktschätzung
- Die Punktschätzung ist die Differenz zwischen einem Paar von Mittelwerten; sie wird anhand der Stichprobendaten berechnet. Das Konfidenzintervall wird um diesen Wert zentriert.
- Fehlerspanne
- Die Fehlerspanne definiert die Breite des Konfidenzintervalls, und sie wird durch die beobachtete Streuung in der Stichprobe, den Stichprobenumfang und das Konfidenzniveau bestimmt. Zum Berechnen der Obergrenze des Konfidenzintervalls wird die Fehlerspanne zur Punktschätzung addiert. Zum Berechnen der Untergrenze des Konfidenzintervalls wird die Fehlerspanne von der Punktschätzung subtrahiert. Die Spanne wird mit zunehmender Anzahl von Vergleichen breiter, um das simultane Konfidenzniveau beizubehalten, auf dem alle Intervalle die tatsächlichen Differenzen der Grundgesamtheiten enthalten.
Interpretation
Verwenden Sie die Konfidenzintervalle, um die Differenzen zwischen den Gruppenmittelwerten auszuwerten.
Simultane Tukey-Tests für Differenzen der Mittelwerte
| Differenz der Stufen | Differenz der Mittelwerte | SE der Differenz | 95%-KI | t-Wert | Korrigierter p-Wert |
|---|---|---|---|---|---|
| Mischung 2 - Mischung 1 | -6,17 | 2,28 | (-12,55; 0,22) | -2,70 | 0,061 |
| Mischung 3 - Mischung 1 | -1,75 | 2,28 | (-8,14; 4,64) | -0,77 | 0,868 |
| Mischung 4 - Mischung 1 | 3,33 | 2,28 | (-3,05; 9,72) | 1,46 | 0,478 |
| Mischung 3 - Mischung 2 | 4,42 | 2,28 | (-1,97; 10,80) | 1,94 | 0,245 |
| Mischung 4 - Mischung 2 | 9,50 | 2,28 | (3,11; 15,89) | 4,17 | 0,002 |
| Mischung 4 - Mischung 3 | 5,08 | 2,28 | (-1,30; 11,47) | 2,23 | 0,150 |
- Das Konfidenzintervall für die Differenz zwischen den Mittelwerten von Mischung 2 und Mischung 4 erstreckt sich von 3,11 bis 15,89. Dieser Bereich enthält nicht den Wert null, was darauf hinweist, dass die Differenz statistisch signifikant ist.
- Die Konfidenzintervalle für alle weiteren Mittelwertpaare enthalten den Wert null, was darauf hinweist, dass die Differenzen statistisch nicht signifikant sind.
- Das simultane 95%-Konfidenzniveau gibt an, dass Sie sich zu 95 % sicher sein können, dass alle dieser Konfidenzintervalle die tatsächlichen Differenzen enthalten.
- Das individuelle 98,89%-Konfidenzniveau gibt an, dass Sie sich zu 98,89 % sicher sein können, dass jedes Konfidenzintervall die tatsächliche Differenz für den betreffenden Vergleich enthält.
t-Wert
Der t-Wert ist eine Teststatistik, mit der das Verhältnis zwischen der Differenz zwischen den Mittelwerten und dem Standardfehler der Differenz gemessen wird.
Interpretation
Sie können anhand des t-Werts feststellen, ob die Nullhypothese, die besagt, dass die Differenz zwischen den Mittelwerten gleich 0 ist, zurückgewiesen werden sollte. Häufiger wird jedoch der p-Wert verwendet, da er leichter zu interpretieren ist. Weitere Informationen zum Verwenden des kritischen Werts finden Sie unter Verwenden des t-Werts, um zu bestimmen, ob die Nullhypothese zurückzuweisen ist.
Minitab verwendet den t-Wert, um den p-Wert zu berechnen.
Korrigierter p-Wert
Der korrigierte p-Wert gibt an, welche Paare in einer Familie von Vergleichen signifikant unterschiedlich sind. Die Korrektur begrenzt die simultane Irrtumswahrscheinlichkeit auf das von Ihnen angegebene Alpha-Niveau. Wenn Sie für Mehrfachvergleiche einen normalen p-Wert verwenden, steigt die simultane Irrtumswahrscheinlichkeit mit jedem weiteren Vergleich.
Bei Mehrfachvergleichen ist es wichtig, die simultane Irrtumswahrscheinlichkeit zu berücksichtigten, weil die Wahrscheinlichkeit eines Fehlers 1. Art bei einer Serie von Vergleichen größer als die Irrtumswahrscheinlichkeit für einen Vergleich alleine ist.
Interpretation
Wenn der korrigierte p-Wert kleiner als Alpha ist, weisen Sie die Nullhypothese zurück und schlussfolgern, dass die Differenz zwischen einem Paar von Gruppenmittelwerten statistisch signifikant ist. Der korrigierte p-Wert stellt außerdem die kleinste simultane Irrtumswahrscheinlichkeit dar, bei der eine bestimmte Nullhypothese verworfen wird.
Fehlerbalkendiagramm für Differenzen der Mittelwerte
Verwenden Sie die Konfidenzintervalle, um wahrscheinliche Bereiche für die Differenzen zu ermitteln und die praktische Signifikanz der Differenzen zu beurteilen. Die Grafik zeigt eine Gruppe Konfidenzintervalle für die Differenzen zwischen Paaren von Mittelwerten. Konfidenzintervalle, die den Wert null nicht enthalten, weisen auf eine statistisch signifikante Mittelwertdifferenz hin.
Je nach gewählter Vergleichsmethode werden im Diagramm unterschiedliche Paare von Gruppen verglichen, und es wird einer der folgenden Typen von Konfidenzintervallen angezeigt.
-
Individuelles Konfidenzniveau
Der Prozentsatz der Fälle, in denen ein einziges Konfidenzintervall die tatsächliche Differenz zwischen einem Paar von Gruppenmittelwerten enthalten würde, wenn die Untersuchung mehrmals wiederholt werden würde.
-
Simultanes Konfidenzniveau
Der Prozentsatz der Fälle, in denen eine Gruppe von Konfidenzintervallen die tatsächlichen Differenzen für alle Gruppenvergleiche enthalten würde, wenn die Untersuchung mehrmals wiederholt werden würde.
Insbesondere bei mehreren Vergleichen ist es wichtig, das simultane Konfidenzniveau unter Kontrolle zu halten. Wenn das simultane Konfidenzniveau nicht unter Kontrolle ist, nimmt mit der Anzahl der Vergleiche die Wahrscheinlichkeit zu, das mindestens ein Konfidenzintervall nicht die tatsächliche Differenz enthält.
Interpretation
- Das Konfidenzintervall für die Differenz zwischen den Mittelwerten von Mischung 4 und Mischung 2 erstreckt sich von 3,11 bis 15,89. Dieser Bereich enthält nicht den Wert null, was darauf hinweist, dass die Differenz zwischen diesen Mittelwerten statistisch signifikant ist.
- Die Konfidenzintervalle für alle weiteren Mittelwertpaare enthalten den Wert null, was darauf hinweist, dass die Differenzen statistisch nicht signifikant sind.
- Das simultane 95%-Konfidenzniveau gibt an, dass Sie sich zu 95 % sicher sein können, dass alle dieser Konfidenzintervalle die tatsächlichen Differenzen enthalten.
- Jedes individuelle Konfidenzintervall verfügt über ein Konfidenzniveau von 98,89 %. Dieses Ergebnis deutet darauf hin, dass Sie sich zu 98,89 % sicher sein können, dass jedes individuelle Intervall die tatsächliche Differenz zwischen einem spezifischen Paar von Gruppenmittelwerten enthält. Die individuellen Konfidenzniveaus für die einzelnen Vergleiche erzeugen das simultane 95%-Konfidenzniveau für alle sechs Vergleiche.
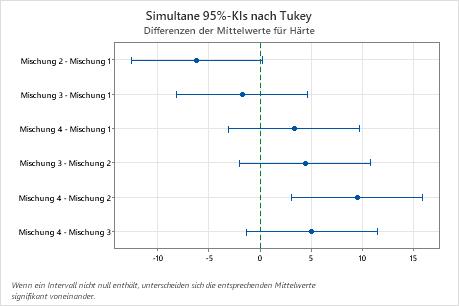
Simultane Tukey-Tests für Differenzen der Mittelwerte
| Differenz der Stufen | Differenz der Mittelwerte | SE der Differenz | 95%-KI | t-Wert | Korrigierter p-Wert |
|---|---|---|---|---|---|
| Mischung 2 - Mischung 1 | -6,17 | 2,28 | (-12,55; 0,22) | -2,70 | 0,061 |
| Mischung 3 - Mischung 1 | -1,75 | 2,28 | (-8,14; 4,64) | -0,77 | 0,868 |
| Mischung 4 - Mischung 1 | 3,33 | 2,28 | (-3,05; 9,72) | 1,46 | 0,478 |
| Mischung 3 - Mischung 2 | 4,42 | 2,28 | (-1,97; 10,80) | 1,94 | 0,245 |
| Mischung 4 - Mischung 2 | 9,50 | 2,28 | (3,11; 15,89) | 4,17 | 0,002 |
| Mischung 4 - Mischung 3 | 5,08 | 2,28 | (-1,30; 11,47) | 2,23 | 0,150 |
