In diesem Thema
Boxplot
Ein Boxplot ist eine grafische Zusammenfassung der Verteilung der einzelnen Stichproben. Mit dem Boxplot lassen sich die Form, Zentraltendenz und Streuung der Stichproben leicht vergleichen.
Interpretation
Verwenden Sie ein Boxplot, um die Streubreite der Daten zu untersuchen und um potenzielle Ausreißer zu identifizieren. Boxplots empfehlen sich insbesondere für Stichprobenumfänge größer als 20.
- Schiefe Daten
-
Untersuchen Sie die Streubreite der Daten, um zu ermitteln, ob die Daten schief sind. Wenn die Daten schief sind, liegen die meisten Datenwerte am oberen oder unteren Rand der Grafik. Schiefe Daten weisen darauf hin, dass die Daten möglicherweise nicht normalverteilt sind. Häufig lässt sich die Schiefe am einfachsten mit einem Einzelwertdiagramm, einem Histogramm oder einem Boxplot erkennen.
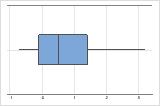
Rechtsschief
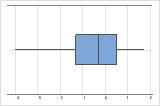
Linksschief
Das Boxplot mit rechtsschiefen Daten zeigt durchschnittliche Wartezeiten. Der Großteil der Wartezeiten ist relativ kurz, und nur wenige Wartezeiten sind länger. Das Boxplot mit linksschiefen Daten zeigt Ausfallraten. Einige Elemente fallen sofort aus, deutlich mehr Elemente fallen später aus.
Stark schiefe Daten können die Gültigkeit des p-Werts beeinträchtigen, wenn die Stichprobe klein ist (< 20 Werte). Wenn die Daten stark schief sind und eine kleine Stichprobe vorliegt, erwägen Sie, den Stichprobenumfang zu vergrößern.
- Ausreißer
-
Ausreißer, d. h. Datenwerte, die weit entfernt von den anderen Datenwerten liegen, können sich stark auf Ihre Ergebnisse auswirken. Häufig lassen sich Ausreißer am einfachsten in einem Boxplot erkennen.
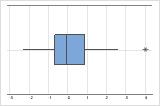
In einem Boxplot werden Ausreißer mit einem Sternchen (*) gekennzeichnet.
Versuchen Sie, die Ursache für die Ausreißer zu ermitteln. Korrigieren Sie sämtliche Dateneingabe- oder Messfehler. Erwägen Sie, Datenwerte zu entfernen, die auf ungewöhnliche, einmalige Ereignisse (Ausnahmebedingungen) zurückzuführen sind. Wiederholen Sie anschließend die Analyse.
Einzelwertdiagramm
In einem Einzelwertdiagramm werden die Einzelwerte in jeder Stichprobe gezeigt. Mit einem Einzelwertdiagramm lassen sich die Stichproben leicht vergleichen. Jeder Kreis stellt eine Beobachtung dar. Die Verwendung eines Einzelwertdiagramms empfiehlt sich insbesondere bei kleinen Stichprobenumfängen.
Interpretation
Verwenden Sie ein Einzelwertdiagramm, um die Streubreite der Daten zu untersuchen und potenzielle Ausreißer zu identifizieren. Einzelwertdiagramme empfehlen sich insbesondere für Stichprobenumfänge kleiner als 50.
- Schiefe Daten
-
Untersuchen Sie die Streubreite der Daten, um zu ermitteln, ob die Daten schief sind. Wenn die Daten schief sind, liegen die meisten Datenwerte am oberen oder unteren Rand der Grafik. Schiefe Daten weisen darauf hin, dass die Daten möglicherweise nicht normalverteilt sind. Häufig lässt sich die Schiefe am einfachsten mit einem Einzelwertdiagramm, einem Histogramm oder einem Boxplot erkennen.
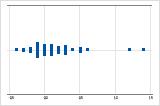
Rechtsschief

Linksschief
Das Einzelwertdiagramm mit rechtsschiefen Daten zeigt Wartezeiten. Der Großteil der Wartezeiten ist relativ kurz, und nur wenige Wartezeiten sind länger. Das Einzelwertdiagramm mit linksschiefen Daten zeigt Ausfallzeiten. Einige Elemente fallen sofort aus, deutlich mehr Elemente fallen später aus.
- Ausreißer
-
Ausreißer, d. h. Datenwerte, die weit entfernt von den anderen Datenwerten liegen, können sich stark auf Ihre Ergebnisse auswirken. Häufig lassen sich Ausreißer einfach in einem Einzelwertdiagramm erkennen.
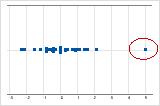
In einem Einzelwertdiagramm weisen ungewöhnlich hohe oder niedrige Datenwerte auf mögliche Ausreißer hin.
Versuchen Sie, die Ursache für die Ausreißer zu ermitteln. Korrigieren Sie sämtliche Dateneingabe- oder Messfehler. Erwägen Sie, Datenwerte zu entfernen, die auf ungewöhnliche, einmalige Ereignisse (Ausnahmebedingungen) zurückzuführen sind. Wiederholen Sie anschließend die Analyse.
Fehlerbalkendiagramm
Verwenden Sie das Fehlerbalkendiagramm, um den Mittelwert und das Konfidenzintervall für jede Gruppe anzuzeigen.
- Jeder Punkt stellt einen Stichprobenmittelwert dar.
- Jedes Intervall ist ein individuelles 95%-Konfidenzintervall für den Mittelwert einer Gruppe. Sie können sich zu 95 % sicher sein, dass der Gruppenmittelwert im Konfidenzintervall der Gruppe enthalten ist.
Wichtig
Interpretieren Sie diese Intervalle mit Vorsicht, da die Wahrscheinlichkeit eines Fehlers 1. Art ansteigt, wenn Sie Mehrfachvergleiche ausführen. Das heißt, je mehr Vergleiche Sie ausführen, desto höher ist die Wahrscheinlichkeit, dass bei mindestens einem Vergleich fälschlicherweise geschlussfolgert wird, dass eine der beobachteten Differenzen signifikant abweicht.
Interpretation
In diesen Ergebnissen weist Mischung 2 den kleinsten und Mischung 4 den größten Mittelwert auf. Sie können anhand dieser Grafik nicht ermitteln, ob Differenzen statistisch signifikant sind. Um die statistische Signifikanz zu bestimmen, untersuchen Sie die Konfidenzintervalle für die Differenzen der Mittelwerte.