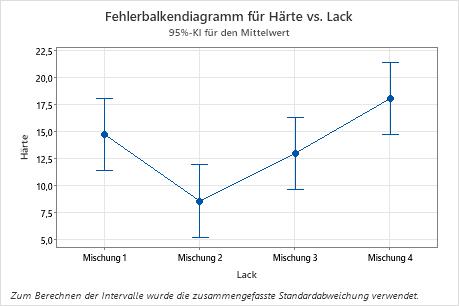
Ein Chemotechniker möchte die Härte von vier Lackmischungen miteinander vergleichen. Sechs Stichproben jeder Lackmischung wurden auf ein Metallstück aufgetragen. Der Lacküberzug der einzelnen Metallstücke wurde ausgehärtet. Anschließend wurde die Härte jeder Stichprobe gemessen. Um die Gleichheit der Mittelwerte zu testen und die Differenzen zwischen Paaren von Mittelwerten zu untersuchen, führt der Analytiker eine einfache ANOVA mit Mehrfachvergleichen aus.
- Öffnen Sie die Beispieldaten Lackhärte.MWX.
- Wählen Sie aus.
- Wählen Sie Antwortdaten befinden sich für alle Faktorstufen in einer Spalte aus.
- Geben Sie im Feld Antwort die Spalte Härte ein.
- Geben Sie im Feld Faktor die Spalte Lack ein.
- Klicken Sie auf die Schaltfläche Vergleiche, und wählen Sie Tukey aus.
- Klicken Sie in den einzelnen Dialogfeldern auf OK.
Interpretieren der Ergebnisse
Der p-Wert aus der ANOVA der Lackhärte ist kleiner als 0,05. Dieses Ergebnis verweist darauf, dass sich die Härten der Lackmischungen signifikant voneinander unterscheiden. Dem Techniker ist bekannt, dass sich einige der Gruppenmittelwerte voneinander unterscheiden.
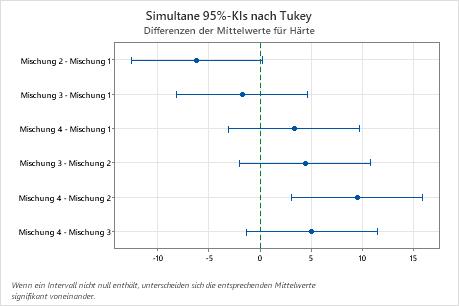
Der Techniker testet anhand der Ergebnisse des Tukey-Vergleichs formal, ob die Differenz zwischen einem Paar von Gruppen statistisch signifikant ist. Die Grafik mit den simultanen Tukey-Konfidenzintervallen veranschaulicht, dass sich das Konfidenzintervall für die Differenz zwischen den Mittelwerten von Mischung 2 und Mischung 4 von 3,114 bis 15,886 erstreckt. Dieser Bereich enthält nicht den Wert null, was darauf hinweist, dass die Differenz zwischen diesen Mittelwerten signifikant ist. Der Techniker kann anhand dieses Schätzwertes der Differenz beurteilen, ob die Differenz praktisch signifikant ist.
Die Konfidenzintervalle für alle weiteren Mittelwertpaare enthalten den Wert null, was darauf hinweist, dass die Differenzen nicht signifikant sind.
Der niedrige Wert des prognostizierten R2 (24,32 %) weist darauf hin, dass das Modell unpräzise Prognosen für neue Beobachtungen generiert. Diese mangelhafte Präzision kann auf die kleine Größe der Gruppen zurückzuführen sein. Daher sollte der Techniker auf Grundlage des Modells keine verallgemeinernden Aussagen über die Stichprobendaten hinaus treffen.
Methode
| Nullhypothese | Alle Mittelwerte sind gleich. |
|---|
| Alternativhypothese | Nicht alle Mittelwerte sind gleich. |
|---|
| Signifikanzniveau | α = 0,05 |
|---|
Faktorinformationen
| Lack | 4 | Mischung 1; Mischung 2; Mischung 3; Mischung 4 |
|---|
Varianzanalyse
| Lack | 3 | 281,7 | 93,90 | 6,02 | 0,004 |
|---|
| Fehler | 20 | 312,1 | 15,60 | | |
|---|
| Gesamt | 23 | 593,8 | | | |
|---|
Zusammenfassung des Modells
| 3,95012 | 47,44% | 39,56% | 24,32% |
Mittelwerte
| Mischung 1 | 6 | 14,73 | 3,36 | (11,37; 18,10) |
|---|
| Mischung 2 | 6 | 8,57 | 5,50 | (5,20; 11,93) |
|---|
| Mischung 3 | 6 | 12,98 | 3,73 | (9,62; 16,35) |
|---|
| Mischung 4 | 6 | 18,07 | 2,64 | (14,70; 21,43) |
|---|
Gruppierungsinformationen anhand der Tukey-Methode und 95%-Konfidenz
| Mischung 4 | 6 | 18,07 | A | |
|---|
| Mischung 1 | 6 | 14,73 | A | B |
|---|
| Mischung 3 | 6 | 12,98 | A | B |
|---|
| Mischung 2 | 6 | 8,57 | | B |
|---|