In diesem Thema
Varianzkomponenten
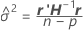
wobei 

Weitere Informationen zum Schätzen von θi finden Sie in [1].
Weitere Einzelheiten zur Notation finden Sie im Abschnitt „Methoden“.
Literaturhinweise
- Hemmerle, W. und Hartley, H. (1973). Computing Maximum Likelihood Estimates for the Mixed A.O.V. Model using the W transformation. Technometrics, 15(4): S. 819-831.
Standardfehler von Varianzkomponenten
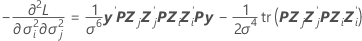
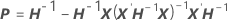
 Spalte, j = 1, …, c:
Spalte, j = 1, …, c:
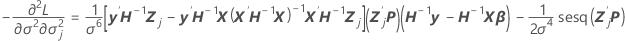

Diese Komponente entspricht zudem dem Wert der letzten Spalte und der  Zeile durch die Symmetrieeigenschaft der Varianz-Kovarianz-Matrix.
Zeile durch die Symmetrieeigenschaft der Varianz-Kovarianz-Matrix.

Die asymptotische Varianz-Kovarianz-Matrix für die Schätzwerte der Varianzkomponenten beläuft sich auf das Doppelte der Umkehrung der beobachteten Fisher-Informationsmatrix. Die Schätzwerte der Standardfehler sind die Quadratwurzeln der Diagonalelemente der Varianz-Kovarianz-Matrix. Die ersten c Diagonalelemente stehen für die Varianzkomponenten der Terme der Zufallseffekte. Das letzte Diagonalelement ist für die Fehlervarianzkomponente bestimmt.
Notation
| Begriff | Beschreibung |
|---|---|
 | Spur der Matrix  |
 | die Summe der Quadrate aller Elemente in der Matrix M |
Weitere Einzelheiten zur Notation finden Sie im Abschnitt „Methoden“.
Konfidenzintervalle für Varianzkomponenten
Minitab verwendet die Delta-Methode, um Konfidenzgrenzen nach Wald für den natürlichen Logarithmus der Varianzkomponenten zu konstruieren, und potenziert dann die Konfidenzintervalle für die Varianzkomponenten. Die Formeln für die Varianzkomponente für Fehler weisen die gleiche Form auf.
Beidseitiges Intervall
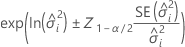
Untergrenze
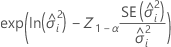
Obergrenze
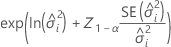
Notation
| Begriff | Beschreibung |
|---|---|
 | das 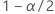 -Quantil aus der Standardnormalverteilung -Quantil aus der Standardnormalverteilung |
 | 1 − Konfidenzniveau |
 | der Standardfehler der  Varianzkomponente Varianzkomponente |
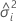 | die Varianzkomponente für den  Term mit Zufallseffekten Term mit Zufallseffekten |
z-Wert und p-Wert
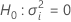
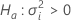


Notation
| Begriff | Beschreibung |
|---|---|
| z | Wert der inversen kumulativen Verteilungsfunktion für die Standardnormalverteilung |
Varianz-Kovarianz-Matrix
 Komponente der beobachteten Fisher-Informationsmatrix:
Komponente der beobachteten Fisher-Informationsmatrix:
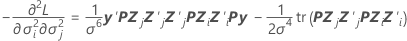

 Spalte, j = 1, …, c:
Spalte, j = 1, …, c:
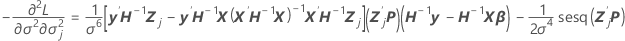

Diese Komponente entspricht zudem dem Wert der letzten Spalte und der  Zeile durch die Symmetrieeigenschaft der Varianz-Kovarianz-Matrix.
Zeile durch die Symmetrieeigenschaft der Varianz-Kovarianz-Matrix.

Notation
| Begriff | Beschreibung |
|---|---|
 | Spur der Matrix  |
Weitere Einzelheiten zur Notation finden Sie im Abschnitt „Methoden“.
