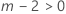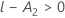In diesem Thema
Tests von Termen mit festen Effekten
Bei den Tests der Terme mit festen Effekten handelt es sich um F-Tests. Die Nullhypothese für den Test hängt davon ab, ob sich der Test auf einen Term mit festem Faktor oder einen Kovariatenterm bezieht. Für einen Term mit einem festen Faktor besagt die Nullhypothese, dass der Term keine signifikante Auswirkung auf die Antwortvariable hat. Für einen Kovariatenterm besagt die Nullhypothese, dass zwischen der Antwortvariablen und dem Kovariatenterm keine Assoziation besteht.
Minitab bietet zwei Methoden zum Testen von Termen mit festem Effekt: die Kenward-Roger-Approximation und die Satterthwaite-Approximation. Weitere Informationen zur Kenward-Roger-Approximation finden Sie in Kenward und Roger.1 Weitere Informationen zur Satterthwaite-Approximation finden Sie in Giesbrecht und Burns 2 sowie in Fai und Cornelius. 3
Die Berechnung der Freiheitsgrade des Nenners für die F-Statistik und die Berechnung der F-Statistik unterscheiden sich. Die Berechnung der Freiheitsgrade des Zählers und die Ermittlung eines p-Werts für eine bestimmte F-Statistik sind für beide Methoden gleich.
Kenward-Roger-Approximation
Die Kenward-Roger-Approximation ist eine Methode zum Untersuchen der statistischen Signifikanz von Termen mit festen Effekten.
F-Statistik
Dabei gilt Folgendes:
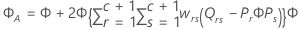
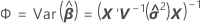
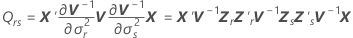
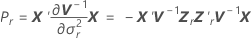
Notation
| Begriff | Beschreibung |
|---|---|
| l | die Freiheitsgrade des Zählers, die der Anzahl der Parameter im zu testenden Term entsprechen |
| 0 | die Matrix mit 0 Komponenten |
| Il | die Identitätsmatrix mit l-Dimension |
| c + 1 | die Anzahl der Varianzkomponenten |
| wrs | (r, s)-te Komponente der asymptotischen Varianz-Kovarianz-Matrix von  |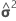
| V−1 | Inverse der Varianz-Kovarianz-Matrix |
Weitere Einzelheiten zur Notation finden Sie im Abschnitt „Methoden“.
Freiheitsgrade des Nenners
Dabei gilt Folgendes:
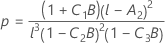
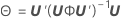
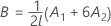
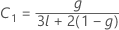
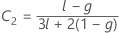
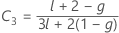
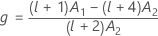
λ nach Kenward und Roger
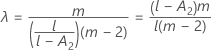
Wenn eine der Bedingungen nicht zutrifft, ist λ = 1.
Gemäß der Nullhypothese folgt Lambda × F einer asymptotischen F-Verteilung mit Freiheitsgraden des Zählers und Freiheitsgraden des Nenners. Diese Eigenschaft wird bei der Berechnung des p-Werts verwendet.
Satterthwaite-Approximation
Die Satterthwaite-Approximation ist eine Methode zum Untersuchen der statistischen Signifikanz von Termen mit festen Effekten.
F-Statistik
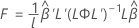
wobei L und 
die gleichen Definitionen wie in der Kenward-Roger-Approximation aufweisen.
Freiheitsgrade des Nenners
Der Prozess zum Bestimmen der Freiheitsgrade umfasst mehrere Schritte.
-
Führen Sie die Spektralzerlegung für die Varianz des geschätzten Vektors des Parameters mit festem Effekt durch:
Hierbei ist P eine orthogonale Matrix der Eigenvektoren und D ist eine Diagonalmatrix von Eigenwerten, beide jeweils mit Dimension l × l.
-
Definieren Sie lr als r-te Zeile von P'L, r = 1, ..., l, und es sei
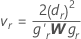wobei dr das r-te Diagonalelement von D, W die asymptotische Varianz-Kovarianz-Matrix von
und gr der Gradientenvektor der folgenden Elemente sind:
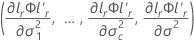
Dabei gilt Folgendes:
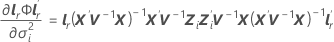
i = 1, …, c und
-
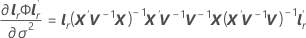
Sei
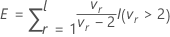
wobei
ist eine Indikatorfunktion zum Eliminieren von Termen mit 
-
Die Freiheitsgrade für den Nenner hängen vom Wert von E ab.
- Wenn E > l, gilt für die Freiheitsgrade Folgendes:
- Andernfalls sind DF des Nenners = 1
- Wenn E > l, gilt für die Freiheitsgrade Folgendes:
Freiheitsgrade des Zählers (DF des Zählers)
| Effekt | DF |
|---|---|
| Fester Faktor |  |
| Kovariate | 1 |
| Wechselwirkungen, die feste Faktoren umfassen |  |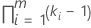
Notation
| Begriff | Beschreibung |
|---|---|
| k | die Anzahl der Stufen im Term mit festem Faktor |
| m | die Anzahl der Faktoren in der Wechselwirkung |
p-Wert – Tests auf feste Effekte
Notation
| Begriff | Beschreibung |
|---|---|
 | die kumulative Verteilungsfunktion der F-Verteilung, deren Freiheitsgrade gleich DF des Zählers bzw. DF des Nenners sind |
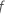 | der berechnete F-Wert für einen Term |
