In diesem Thema
Das Modell mit gemischten Effekten und Log-Likelihood
Die allgemeine Form des Modells mit gemischten Effekten
Modelle mit gemischten Effekten enthalten sowohl feste Effekte als auch Zufallseffekte. Die allgemeine Form des Modells mit gemischten Effekten sieht wie folgt aus:
y = Xβ + Z1μ1 + Z2μ2 + ... + Zcμc + ε
Notation
| Begriff | Beschreibung |
|---|---|
| y | (n x 1)-Vektor von Werten der Antwortvariablen |
| x | die n x p-Designmatrix für die Terme der festen Effekte, p ≤ n |
| β | ein (p x 1)-Vektor von unbekannten Parametern |
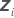 | die n x mi-Designmatrix für den  Zufallsterm im Modell Zufallsterm im Modell |
| μi | ein mi x 1-Vektor von unabhängigen Variablen aus N(0,  ) ) |
| ε | ein n x 1-Vektor von unabhängigen Variablen aus N(0,  ) ) |
| n | Anzahl der Beobachtungen |
| p | die Anzahl der Parameter in  |
| c | die Anzahl der Zufallsterme im Modell |
Varianz-Kovarianz-Matrix
Auf Grundlage der Modellannahme für die allgemeine Form des Modells mit gemischten Effekten weist der Vektor der Antwortvariablen, y, eine multivariate Normalverteilung mit dem mittleren Vektor Xβ und die folgende Varianz-Kovarianz-Matrix auf:
V(σ2) = V(σ2, σ21, ... , σ2c) = σ2In + σ21Z1Z'1 + ... + σ2cZcZ'c
Dabei gilt Folgendes:
σ2 = (σ2, σ21, ... , σ2c)'
σ2, σ21, ... , σ2c werden als Varianzkomponenten bezeichnet.
Durch Faktorisieren ausgehend von der Varianz kann eine Darstellung von H(θ) gefunden werden, die sich in der Berechnung der Log-Likelihood von Modellen mit gemischten Effekten befindet.
V(σ2) = σ2H(θ) = σ2[In + θ1Z1Z'1 + ... + θcZcZ'c]
Notation
| Begriff | Beschreibung |
|---|---|
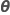 | 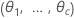 |
| θi | 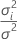 , das Varianzverhältnis des , das Varianzverhältnis des  Zufallsterms über der Fehlervarianz Zufallsterms über der Fehlervarianz |
Log-Likelihood


Notation
| Begriff | Beschreibung |
|---|---|
| H | In + θ1Z1Z'1 + ... + θcZcZ'c |
| |H| | die Determinante von H |
| H-1 | die Inverse von H |
| mi | die Anzahl der Stufen für den  Zufallsterm Zufallsterm |
 | Varianzkomponente für Fehler |
| In | Identitätsmatrix mit n Zeilen und Spalten |
Eingeschränkte Maximum-Likelihood-Schätzung (Restricted Maximum Likelihood, REML)
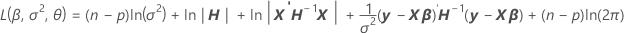
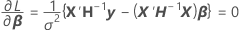
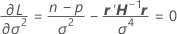
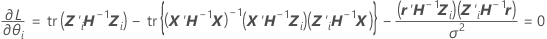
wobei 
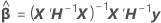
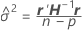
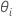 kann nicht explizit aufgelöst werden für
kann nicht explizit aufgelöst werden für 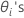 . Minitab verwendet die Newton-Methode zum Schätzen von
. Minitab verwendet die Newton-Methode zum Schätzen von 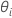 und führt dabei die folgenden Schritte aus:
und führt dabei die folgenden Schritte aus:
- Verwenden der MINQUE-Methode (quadratische erwartungstreue Schätzung mit minimaler Norm)12 der Varianzkomponenten, um die Anfangswerte von σ2 und θi zu berechnen.
- Schätzen von β und σ2 mit den Gleichungen für
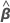 und
und 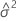 .
. - Ermitteln von θi mit der Newton-Methode, um L(β, σ2, θ) zu minimieren.
- Wiederholen Sie die Schritte 2 und 3 bis zum Erreichen der Konvergenz.
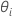 sind die Schätzwerte für das Varianzverhältnis. Die Varianzkomponente für den
sind die Schätzwerte für das Varianzverhältnis. Die Varianzkomponente für den  Zufallsterm wird wie folgt ausgedrückt:
Zufallsterm wird wie folgt ausgedrückt:

Notation
| Begriff | Beschreibung |
|---|---|
| tr(·) | Spur der Matrix |
| X' | Transposition von X |
