In diesem Thema
Bedingter angepasster Wert
Angenommen, ein Modell enthält die zwei Faktoren A und B sowie die Wechselwirkung zwischen den beiden Faktoren A*B. A ist ein Zufallsfaktor, während B einen festen Faktor darstellt.
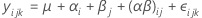
Dabei gilt Folgendes:
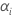ist für den Zufallsfaktor A, 
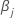ist für den festen Faktor B,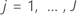 
ist für den Term AB
ist für den Fehlerterm
Die Gleichung für den bedingten angepassten Wert für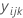 
lautet wie folgt:
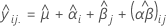
wobei 
und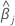 
stellen die entsprechenden berechneten Koeffizienten für die Terme mit festen Effekten dar. Außerdem si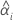nd 
und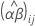 
die berechneten BLUP-Werte für die Zufallsterme.
Mittelwert von AB
Der berechnete Mittelwert von AB auf Stufe i von Faktor A und Stufe j von Faktor B beträgt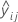 
.
Mittelwert von A
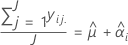
Mittelwert von B
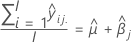
Allgemeine Formel für Mittelwerte
wobei 
ist der berechnete Vektor der Koeffizienten,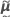 
ist der berechnete BLUP-Vektor 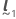und 
und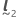 
sind bekannte Vektoren, die durch den Mittelwert für einen bestimmten Term bestimmt werden. Die Mittelwertformel weist in diesem Fall dieselbe Form wie die bedingte Anpassung auf. Daher werden die Formeln für den Standardfehler, die Freiheitsgrade, das Konfidenzintervall, den t-Wert und den p-Wert für den Mittelwert auf die gleiche Weise abgeleitet wie die entsprechenden Formeln für die bedingten Anpassungen. Weitere Informationen zu diesen Formeln für die bedingten Anpassungen finden Sie unter Methoden und Formeln für bedingte Anpassungen und Residuen in Modell mit gemischten Effekten anpassen. Durch Ersetzen des Vektors 
und des Vektors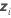 
durch den Vektor 
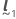und den Vektor 
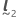in den Formeln für die bedingten Anpassungen erhalten Sie die entsprechenden Formeln für den Mittelwert.
