In diesem Thema
Bedingter angepasster Wert
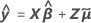
Weitere Einzelheiten zur Notation finden Sie in den Abschnitten „Methoden“, „Test von festen Effekten“ und „Prognosen für Zufallseffekte“.
Standardfehler des bedingten angepassten Werts (SE Anpassung)
Die Standardfehler der bedingten angepassten Werte entsprechen den Quadratwurzeln der Diagonalelemente der folgenden Matrix:
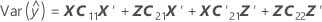
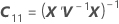
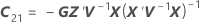

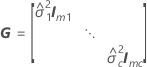
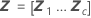
Konfidenzintervalle für bedingte Mittelwerte
Der Bereich, in dem der Mittelwert der Antwortvariablen bei einer gegebenen Gruppe von Werten der Prädiktorvariablen erwartet wird.

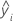 ist die bedingte Anpassung.
ist die bedingte Anpassung. 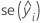 ist der Standardfehler der Anpassung.
ist der Standardfehler der Anpassung.
Bei den Freiheitsgraden wird diese Formel für den bedingten Fall verwendet:
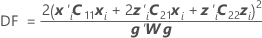
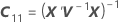
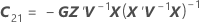

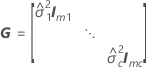
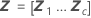
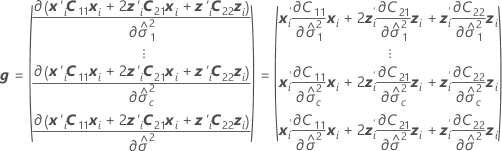
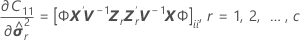
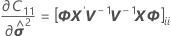

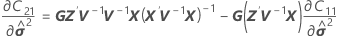
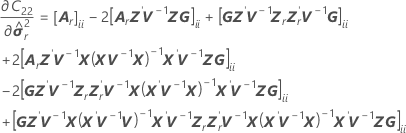
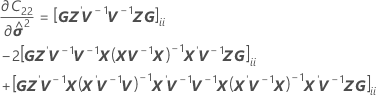
Notation
| Begriff | Beschreibung |
|---|---|
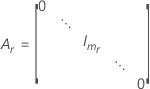
| W | die asymptotische Varianz-Kovarianz-Matrix von 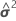 |
Weitere Einzelheiten zur Notation finden Sie im Abschnitt „Methoden“ sowie im Abschnitt „Test von festen Effekten“.
Bedingte Residuen
Ein Residuum ist die Differenz zwischen einem beobachteten Wert und einem angepassten Wert. Dieser Teil der Beobachtung wird durch das angepasste Modell nicht erklärt.
Das  bedingte Residuum wird mit dem folgenden Ausdruck berechnet:
bedingte Residuum wird mit dem folgenden Ausdruck berechnet:
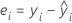
Notation
| Begriff | Beschreibung |
|---|---|
| yi | der  Wert der Antwortvariablen Wert der Antwortvariablen |
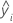 | der  bedingte angepasste Wert bedingte angepasste Wert |
Standardisierte bedingte Residuen

wobei die Standardabweichung des Residuums der entsprechenden diagonalen Quadratwurzel der Varianzmatrix der Residuen entspricht:
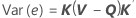
Dabei gilt Folgendes:
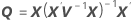


Notation
| Begriff | Beschreibung |
|---|---|
| ei | das  Residuum Residuum |
| Std(ei) | die Standardabweichung des  Residuums Residuums |
