- Varianzschätzung
-
Im Allgemeinen verwenden Sie Eingeschränkte Maximum-Likelihood (REML), da der Schätzwert der Varianzkomponenten aus REML annähernd erwartungstreu, der Maximum-Likelihood-Schätzwert hingegen verzerrt ist. Die systematische Messabweichung nimmt jedoch bei größeren Stichprobenumfängen ab.
Verwenden Sie Maximum-Likelihood (ML), wenn Sie prüfen müssen, ob ein geschachteltes Modell mit einer geringeren Anzahl von Termen mit festen Effekten ebenso gut wie das entsprechende Referenzmodell ist, das mehr Terme mit festen Effekten enthält, wobei beide Modelle die gleiche Anzahl von Zufallstermen und die gleiche Fehlervarianzstruktur aufweisen. Insbesondere sei
die -2 Log-Likelihood aus dem vollständigen Modell und 
die -2 Log-Likelihood aus dem kleineren Modell. Gemäß der Nullhypothese kann asymptotisch
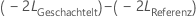auf eine Chi-Quadrat-Verteilung geschlossen werden, deren Freiheitsgrade der Differenz hinsichtlich der Anzahl der Parameter für Terme mit festen Effekten zwischen dem Referenzmodell und dem geschachtelten Modell entsprechen. Sie können mit dem Likelihood-Quotienten-Test bewerten, ob eine Teilmenge von Termen mit festen Effekten aus dem Referenzmodell entfernt werden kann. Weitere Informationen zum Likelihood-Quotienten-Test für feste Parameter in einem Modell mit gemischten Effekten finden Sie in West, Welch und Galecki.1
- DF für feste Effekte
-
Im Allgemeinen verwenden Sie Kenward-Roger-Approximation, da bei den Berechnungen ein korrigierter Schätzwert der Kovarianzmatrix für die Werte der Antwortvariablen verwendet wird, der die systematische Messabweichung aufgrund kleiner Stichprobenumfänge mindert. Sie können auch Satterthwaite-Approximation verwenden. Generell gilt Folgendes: Je größer der Stichprobenumfang, desto kleiner die Differenz zwischen den beiden Methoden.
