In diesem Thema
Randanpassung
Die Randanpassungen stellen Mittelwerte der Antwortvariablen auf verschiedenen Stufen von festen Faktoren dar. Die Randanpassungen werden mit den angepassten Gleichungen der Randwerte berechnet.
SE Anpassung
Der Standardfehler der Anpassung (SE Anpassung) ist ein Schätzwert der Streuung im geschätzten Mittelwert der Antwortvariablen für die angegebenen Variableneinstellungen. Der Standardfehler der Anpassung wird bei der Berechnung des Konfidenzintervalls für den Mittelwert der Antwortvariablen verwendet. Standardfehler sind immer nicht negativ.
DF für den Randmittelwert
Die Freiheitsgrade (DF) entsprechen der Menge an Informationen in den Daten, mit denen das Konfidenzintervall für den Mittelwert der Antwortvariablen geschätzt wird.
Interpretation
Verwenden Sie die Freiheitsgrade, um zu vergleichen, wie viele Informationen zu verschiedenen Randmittelwerten verfügbar sind. In der Regel führen mehr Freiheitsgrade dazu, dass das Konfidenzintervall für den Mittelwert schmaler als ein Intervall mit weniger Freiheitsgraden ist. Da die Standardfehler der Mittelwerte für verschiedene Beobachtungen unterschiedlich sind, muss das Konfidenzintervall für einen Mittelwert mit mehr Freiheitsgraden nicht zwangsläufig schmaler als ein Konfidenzintervall für einen Mittelwert mit weniger Freiheitsgraden sein.
Konfidenzintervall für Randmittelwert (95%-KI)
Diese Konfidenzintervalle (KI) sind Bereiche von Werten, die wahrscheinlich die entsprechenden Randmittelwerte der Antwortvariablen enthalten.
Da die Stichproben zufällig sind, ist es unwahrscheinlich, dass zwei Stichproben aus einer Grundgesamtheit identische Konfidenzintervalle ergeben. Wenn Sie die Stichprobennahme jedoch viele Male wiederholen, enthält ein gewisser Prozentsatz der resultierenden Konfidenzintervalle den unbekannten Parameter der Grundgesamtheit. Der Prozentsatz dieser Konfidenzintervalle, die den Parameter enthalten, stellt das Konfidenzniveau des Intervalls dar.
Das Konfidenzintervall setzt sich aus den folgenden zwei Teilen zusammen:
Interpretation
Bewerten Sie anhand der Konfidenzintervalle, ob die Randmittelwerte der Antwortvariablen statistisch größer, gleich oder kleiner als ein bestimmter Wert sind. Mithilfe der Konfidenzintervalle können Sie auch einen Bereich von Werten für die entsprechenden unbekannten Randmittelwerte der Antwortvariablen ermitteln.
Randresiduum
Ein Residuum (ei) ist die Differenz zwischen einem beobachteten Wert (y) und dem entsprechenden angepassten Randwert (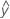 ).
).
Interpretation
Stellen Sie die Residuen grafisch dar, um zu ermitteln, ob das Modell angemessen ist und die Annahmen des Modells mit gemischten Effekten erfüllt. Eine Untersuchung der Residuen kann nützliche Informationen darüber liefern, wie gut das Modell an die Daten angepasst ist. Im Allgemeinen sollten die Residuen zufällig verteilt sein und weder offensichtliche Muster noch ungewöhnliche Werte aufweisen. Wenn Minitab feststellt, dass die Daten ungewöhnliche Beobachtungen enthalten, werden diese Beobachtungen in der Tabelle „Randanpassungen und Bewertung für ungewöhnliche Beobachtungen“ in der Ausgabe identifiziert. Die von Minitab als ungewöhnlich gekennzeichneten Beobachtungen werden durch die vorgeschlagene Gleichung der Randwerte nicht gut modelliert. Es ist jedoch zu erwarten, dass einige ungewöhnliche Beobachtungen vorliegen. Entsprechend den Kriterien für große Residuen ist beispielsweise zu erwarten, dass ca. 5 % der Beobachtungen als Beobachtungen mit einem großen Residuum gekennzeichnet werden.
Std. Resid
Das standardisierte Randresiduum entspricht dem Wert eines Residuums (ei) dividiert durch einen Schätzwert von dessen Standardabweichung.
Interpretation
Verwenden Sie die standardisierten Randresiduen, um Ausreißer zu erkennen. Standardisierte Randresiduen größer als 2 bzw. kleiner als −2 werden im Allgemeinen als groß erachtet. In der Tabelle „Randanpassungen und Bewertung für ungewöhnliche Beobachtungen“ werden die betreffenden Beobachtungen mit einem „R“ gekennzeichnet. Die von Minitab gekennzeichneten Beobachtungen werden durch die vorgeschlagene angepasste Gleichung der Randwerte in der Regel nicht gut modelliert. Es ist jedoch zu erwarten, dass einige ungewöhnliche Beobachtungen vorliegen. Entsprechend den Kriterien für große standardisierte Randresiduen ist beispielsweise zu erwarten, dass ca. 5 % der Beobachtungen als Beobachtungen mit einem großen standardisierten Residuum gekennzeichnet werden.
Standardisierte Randresiduen sind hilfreich, da Roh-Randresiduen u. U. keine geeigneten Anzeichen für Ausreißer darstellen. Die Varianz jedes Roh-Randresiduums kann um die mit ihm verbundenen x-Werte abweichen. Diese ungleiche Streuung erschwert es, die Größen der Roh-Randresiduen zu beurteilen. Durch das Standardisieren der Randresiduen wird dieses Problem behoben, indem die unterschiedlichen Varianzen in eine gemeinsame Skala konvertiert werden.
Hoch (Hebelwirkung)
Mit „Hoch“ können in einem Modell mit gemischten Effekten Datenpunkte mit hohen Hebelwirkungseinstellungen ausschließlich für Terme mit festen Effekten ermittelt werden. Die Designmatrix zum Berechnen von „Hoch“ ist die Designmatrix für Terme mit festen Effekten.
Interpretation
Hoch-Werte liegen zwischen 0 und 1. Minitab kennzeichnet Beobachtungen mit Hebelwirkungswerten von mehr als 3p/n oder, falls kleiner, 0,99 in der Tabelle „Randanpassungen und Bewertung für ungewöhnliche Beobachtungen“ mit einem „X“. Im Ausdruck 3p/n ist p die Anzahl der Koeffizienten im Modell und n die Anzahl der Beobachtungen. Die von Minitab mit einem „X“ gekennzeichneten Beobachtungen können einflussreich sein.
Beobachtungen mit großem Einfluss wirken sich disproportional auf das Modell aus und können irreführende Ergebnisse verursachen. Das Einbinden oder Ausschließen eines einflussreichen Punkts könnte beispielsweise ändern, ob ein Koeffizient statistisch signifikant ist. Beobachtungen mit großem Einfluss können Hebelwirkungspunkte, Ausreißer oder beides sein.
Wenn Sie eine einflussreiche Beobachtung feststellen, ermitteln Sie, ob es sich bei der Beobachtung um einen Dateneingabe- oder Messfehler handelt. Wenn die Beobachtung weder einen Dateneingabefehler noch einen Messfehler darstellt, bestimmen Sie, wie einflussreich die Beobachtung ist. Passen Sie das Modell zuerst mit der Beobachtung und dann ohne die Beobachtung an. Vergleichen Sie anschließend die Koeffizienten, p-Werte, R2-Werte und weitere Modellinformationen. Wenn sich das Modell nach Entfernen der einflussreichen Beobachtung signifikant ändert, untersuchen Sie das Modell eingehender, um festzustellen, ob Sie das Modell falsch angegeben haben. Möglicherweise müssen Sie weitere Daten erfassen, um das Problem zu beheben.
