Ein Wissenschaftler untersucht die Ausbeute von sechs Luzernesorten auf vier zufällig ausgewählten Feldern. Der Ertrag auf den einzelnen Feldern wurde für die einzelnen Sorten aufgezeichnet.
Der Wissenschaftler möchte feststellen, ob sich die Sorte der Luzernepflanzen auf die mittlere Ausbeute auswirkt. Er verfügt über 4 Felder, auf denen er Daten erfassen kann. Der Wissenschaftler möchte jedoch modellieren können, wie die Luzernepflanzen auf Feldern wachsen, die in der Untersuchung nicht eingeschlossen sind. Daher legt er das Feld, auf dem die Luzernepflanzen wachsen, als Zufallsfaktor fest. Der Wissenschaftler verwendet ein Modell mit gemischten Effekten, um sowohl feste als auch zufällige Effekte zu untersuchen.
- Öffnen Sie die Beispieldaten Luzerne.MWX.
- Wählen Sie aus.
- Geben Sie im Feld Antworten die Spalte Ausbeute ein.
- Geben Sie im Feld Zufallsfaktoren (erforderlich) die Spalte Feld ein.
- Geben Sie im Feld Feste Faktoren die Spalte Sorte ein.
- Klicken Sie auf Grafiken.
- Wählen Sie im Feld Residuen für Diagramme die Option Bedingt standardisiert aus.
- Wählen Sie im Feld Residuendiagramme die Option Vier-in-Eins aus.
- Klicken Sie in den einzelnen Dialogfeldern auf OK.
Interpretieren der Ergebnisse
In der Varianzkomponententabelle ist der p-Wert für „Feld“ gleich 0,124. Im Hypothesentest werden keine Hinweise ersichtlich, die darauf hindeuten, dass sich die Varianzkomponente von 0 unterscheidet. Der p-Wert für die Varianzkomponente für Fehler beträgt 0,003. Da der p-Wert kleiner als das Signifikanzniveau 0,05 ist, kann der Wissenschaftler schlussfolgern, dass die Varianzkomponente für Fehler ungleich 0 ist.
Der p-Wert von annähernd 0 für den Term mit festem Faktor „Sorte“ zeigt, dass sich der Effekt von mindestens einer Luzernesorte signifikant von dem der anderen fünf Sorten unterscheidet.
Die Koeffizienten für die Haupteffekte stellen die Differenz zwischen den einzelnen Stufenmittelwerten und dem Gesamtmittelwert dar. Sorte 1 ist beispielsweise einer Luzerneausbeute zugeordnet, die um ca. 0,385 Einheiten über dem Gesamtmittelwert liegt. Der p-Wert von annähernd 0 für diesen Koeffizienten zeigt, dass sich der Effekt von Sorte 1 signifikant vom Effekt einer anderen Stufe des Terms „Stufe“ unterscheidet. Um zu bestimmen, welche Stufeneffekte statistisch gleich sind und welche Stufeneffekte sich statistisch unterscheiden, beabsichtigt der Wissenschaftler, eine Analyse mit Mehrfachvergleichen für den Term durchzuführen.
Der R2-Wert zeigt, dass das Modell ca. 92 % der Streuung in der Ausbeute erklärt. Der Wert von R-Qd(kor) ist mit einem Wert von annähernd 90,2 % ebenfalls hoch. Der Wissenschaftler vergleicht anhand dieses Werts Modelle mit unterschiedlicher Anzahl von Prädiktoren.
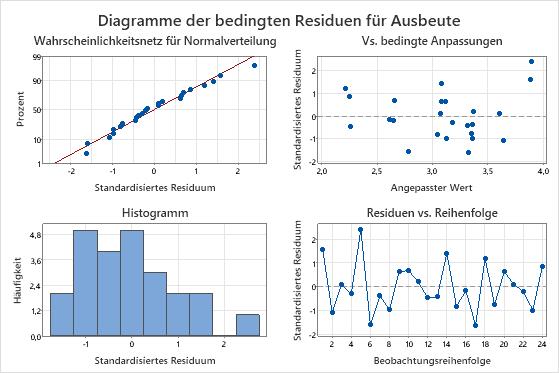
Beobachtungen 1 und 5 sind ungewöhnliche Beobachtungen, da ihre standardisierten Residuen größer als 2 sind. Der Wissenschaftler untersucht die Daten, um sich zu vergewissern, dass die Werte der Antwortvariablen für die betreffenden Beobachtungen korrekt sind.
Die Residuen im Wahrscheinlichkeitsnetz für Normalverteilung folgen annähernd einer Geraden, und die Punkte sind im Diagramm der Residuen vs. Anpassung anscheinend zufällig um 0 gestreut.
Methode
| Varianzschätzung | Eingeschränkte Maximum-Likelihood |
|---|---|
| DF für feste Effekte | Kenward-Roger |
Faktorinformationen
| Faktor | Typ | Stufen | Werte |
|---|---|---|---|
| Feld | Zufällig | 4 | 1; 2; 3; 4 |
| Sorte | Fest | 6 | 1; 2; 3; 4; 5; 6 |
Varianzkomponenten
| Quelle | Var | % von Gesamt | SE Var | z-Wert | p-Wert |
|---|---|---|---|---|---|
| Feld | 0,077919 | 72,93% | 0,067580 | 1,152996 | 0,124 |
| Fehler | 0,028924 | 27,07% | 0,010562 | 2,738613 | 0,003 |
| Gesamt | 0,106843 |
Tests auf feste Effekte
| Term | DF des Zählers | DF des Nenners | F-Wert | p-Wert |
|---|---|---|---|---|
| Sorte | 5,00 | 15,00 | 26,29 | 0,000 |
Zusammenfassung des Modells
| S | R-Qd | R-Qd(kor) | AICc | BIC |
|---|---|---|---|---|
| 0,170071 | 92,33% | 90,20% | 12,54 | 13,52 |
Koeffizienten
| Term | Koef | SE Koef | DF | t-Wert | p-Wert |
|---|---|---|---|---|---|
| Konstante | 3,094583 | 0,143822 | 3,00 | 21,516692 | 0,000 |
| Sorte | |||||
| 1 | 0,385417 | 0,077626 | 15,00 | 4,965016 | 0,000 |
| 2 | 0,145417 | 0,077626 | 15,00 | 1,873287 | 0,081 |
| 3 | 0,107917 | 0,077626 | 15,00 | 1,390205 | 0,185 |
| 4 | -0,319583 | 0,077626 | 15,00 | -4,116938 | 0,001 |
| 5 | 0,395417 | 0,077626 | 15,00 | 5,093838 | 0,000 |
Randanpassungen und Bewertung für ungewöhnliche Beobachtungen
| Beob | Ausbeute | Anpassung | Resid | Std. Resid | |
|---|---|---|---|---|---|
| 1 | 4,100000 | 3,480000 | 0,620000 | 2,190221 | R |
| 5 | 4,220000 | 3,490000 | 0,730000 | 2,578808 | R |
Bedingte Anpassungen und Bewertung für ungewöhnliche Beobachtungen
| Beob | Ausbeute | Anpassung | Resid | Std. Resid | |
|---|---|---|---|---|---|
| 5 | 4,220000 | 3,895339 | 0,324661 | 2,400733 | R |