Wilk-Test
Die Teststatistik, Wilk-Lambda, wird wie folgt ausgedrückt:
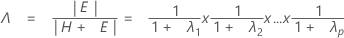
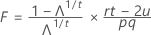
mit pq und (rt – 2u) DF.
Notation
| Begriff | Beschreibung |
|---|---|
| H | Hypothesenmatrix |
| E | Fehlermatrix |
| p | Anzahl der Werte der Antwortvariablen |
| q | DF der Hypothese |
| v | DF für E |
| s | min (p, q) |
| m | 0,5 ( | p – q | – 1) |
| n | 0,5 (v – p – 1) |
| r | v – 0,5 (p – q + 1) |
| u | 0,25(pq – 2) |
| t | = Quadratwurzel ([p2 q2 – 4] / p2 + q2 – 5, wenn p2 + q2 – 5 > 0 |
| t | 1 |
Seien λ1≥λ2≥λ3≥ . . . ≥λp die Eigenwerte von (E** - 1) * H. Die ersten drei Teststatistiken können entweder anhand von H und E oder dieser Eigenwerte ausgedrückt werden.
Die H-Matrix ist eine (p x p)-Matrix, die die Summe der Quadrate „zwischen“ auf der Diagonalen für jede der p Variablen enthält. Die H-Matrix wird wie folgt berechnet:

Die E-Matrix ist eine (p x p)-Matrix, die die Summe der Quadrate „innerhalb“ auf der Diagonalen für jede der p Variablen enthält. Die E-Matrix wird wie folgt berechnet:
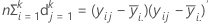
In den ersten drei Tests ist die F-Statistik exakt, wenn s = 1 bzw. 2, andernfalls stellt sie eine Approximation dar. Minitab gibt eine Meldung aus, wenn es sich um einen annähernden Test handelt.
Lawley-Hotelling-Test
Die Teststatistik, die Lawley-Hotelling-Spur, wird wie folgt ausgedrückt:

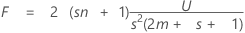
mit s (2m + s + 1) und 2 (sn + 1) DF.
Notation
| Begriff | Beschreibung |
|---|---|
| H | Hypothesenmatrix |
| E | Fehlermatrix |
| p | Anzahl der Antwortvariablen |
| q | DF der Hypothese |
| v | DF für E |
| s | min (p, q) |
| m | 0,5 ( | p – q | – 1) |
| n | 0,5 (v – p – 1) |
| r | v – 0,5 (p – q + 1) |
| u | 0,25(pq – 2) |
| t | = Quadratwurzel ([p2 q2 – 4] / p2 + q2 – 5, wenn p2 + q2 – 5 > 0 |
| t | 1 |
Seien λ1≥λ2≥λ3≥ . . . ≥λp die Eigenwerte von (E** – 1) * H. Die ersten drei Teststatistiken können entweder anhand von H und E oder dieser Eigenwerte ausgedrückt werden.
Die H-Matrix ist eine (p x p)-Matrix, die die Summe der Quadrate „zwischen“ auf der Diagonalen für jede der p Variablen enthält. Die H-Matrix wird wie folgt berechnet:

Die E-Matrix ist eine (p x p)-Matrix, die die Summe der Quadrate „innerhalb“ auf der Diagonalen für jede der p Variablen enthält. Die E-Matrix wird wie folgt berechnet:
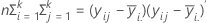
In den ersten drei Tests ist die F-Statistik exakt, wenn s = 1 bzw. 2, andernfalls stellt sie eine Approximation dar. Minitab gibt eine Meldung aus, wenn es sich um einen annähernden Test handelt.
Pillai-Test
Die Teststatistik, die Pillai-Spur, wird wie folgt ausgedrückt:


Notation
| Begriff | Beschreibung |
|---|---|
| H | Hypothesenmatrix |
| E | Fehlermatrix |
| p | Anzahl der Antwortvariablen |
| q | DF der Hypothese |
| v | DF für E |
| s | min (p, q) |
| m | 0,5 ( | p – q | – 1) |
| n | 0,5 (v – p – 1) |
| r | v – 0,5 (p – q + 1) |
| u | 0,25(pq – 2) |
| t | = Quadratwurzel ([p2 q2 – 4] / p2 + q2 – 5, wenn p2 + q2 – 5 > 0 |
| t | 1 |
Seien λ1≥λ2≥λ3≥ . . . ≥λp die Eigenwerte von (E** – 1) * H. Die ersten drei Teststatistiken können entweder anhand von H und E oder dieser Eigenwerte ausgedrückt werden.
Die H-Matrix ist eine (p x p)-Matrix, die die Summe der Quadrate „zwischen“ auf der Diagonalen für jede der p Variablen enthält. Die H-Matrix wird wie folgt berechnet:

Die E-Matrix ist eine (p x p)-Matrix, die die Summe der Quadrate „innerhalb“ auf der Diagonalen für jede der p Variablen enthält. Die E-Matrix wird wie folgt berechnet:
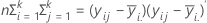
In den ersten drei Tests ist die F-Statistik exakt, wenn s = 1 bzw. 2, andernfalls stellt sie eine Approximation dar. Minitab gibt eine Meldung aus, wenn es sich um einen annähernden Test handelt.
Größte charakteristische Wurzel nach Roy
Hierbei handelt es sich um den größten Eigenwert, λ1. Zum Durchführen des Tests müssen Sie spezielle Diagramme (so genannte Heck-Diagramme) sowie die Parameter s, m, und n verwenden, um das Signifikanzniveau zu ermitteln.
Diese Diagramme finden Sie in Heck1.
Notation
| Begriff | Beschreibung |
|---|---|
| s | min (p, q) |
| m | 0,5 ( | p – q | – 1) |
| n | 0,5 (v – p – 1) |
Seien λ1≥λ2≥λ3≥ . . . ≥λp die Eigenwerte von (E** – 1) * H. Die ersten drei Teststatistiken können entweder anhand von H und E oder dieser Eigenwerte ausgedrückt werden.
- D. L. Heck (1960), „Charts of Some Upper Percentage Points of the Distribution of the Largest Characteristic Root“, The Annals of Statistics, S. 625–642.
