Support für Minitab® 

Interpretieren der wichtigsten Ergebnisse für Allgemeine MANOVA

Weitere Informationen zu Minitab
Führen Sie die folgenden Schritte aus, um die allgemeine MANOVA zu interpretieren. Zu den wichtigsten Ausgaben zählen der p-Wert, die Koeffizienten, R2 und die Residuendiagramme.

In diesem Thema

Schritt 1: Testen der Gleichheit der Mittelwerte aller Antwortvariablen

Wenn Sie die Mittelwerte aller Antwortvariablen gleichzeitig auf Gleichheit prüfen möchten, vergleichen Sie die p-Werte in den MANOVA-Testtabellen für die einzelnen Terme mit dem Signifikanzniveau. In der Regel ist ein Signifikanzniveau (als α oder Alpha bezeichnet) von 0,05 gut geeignet. Ein Signifikanzniveau von 0,05 bedeutet ein Risiko, dass auf eine vorhandene Assoziation geschlossen wird, während tatsächlich keine vorhanden ist, von 5 %.
p-Wert ≤ α: Die Differenzen zwischen den Mittelwerten sind statistisch signifikant.
Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, können Sie schlussfolgern, dass die Differenzen zwischen den Mittelwerten statistisch signifikant sind.
p-Wert > α: Die Differenzen zwischen den Mittelwerten sind statistisch nicht signifikant.
Wenn der p-Wert größer als das Signifikanzniveau ist, können Sie nicht schlussfolgern, dass die Differenzen zwischen den Mittelwerten statistisch signifikant sind. Es empfiehlt sich möglicherweise, dass Modell ohne den Term erneut anzupassen.
Wenn mehrere Prädiktoren ohne eine statistisch signifikante Assoziation mit der Antwortvariablen vorhanden sind, können Sie das Modell reduzieren, indem Sie Terme einzeln nacheinander entfernen. Weitere Informationen zum Entfernen von Termen aus dem Modell finden Sie unter Modellreduzierung.
Wenn ein Modellterm statistisch signifikant ist, hängt die Interpretation von der Art des Terms ab. Die Interpretationen lauten wie folgt:
  • Wenn ein Haupteffekt signifikant ist, unterscheiden sich die Stufenmittelwerte des Faktors für alle Antwortvariablen im Modell signifikant voneinander.
  • Wenn ein Wechselwirkungsterm signifikant ist, unterscheiden sich die Effekte der einzelnen Faktoren auf allen Stufen der anderen Faktoren für alle Antwortvariablen im Modell. Deswegen ist es nicht sinnvoll, die Einzeleffekte von Termen zu analysieren, die Teil einer signifikanten Wechselwirkung höherer Ordnung sind.

MANOVA-Tests für Methode




DF
KriteriumTeststatistikFZählerNennerp
Wilks0,6309916,0822550,000
Lawley-Hotelling0,5848216,0822550,000
Pillai0,3690116,0822550,000
Roy0,58482       
s = 1    m = 0    n = 26,5

MANOVA-Tests für Werk




DF
KriteriumTeststatistikFZählerNennerp
Wilks0,891781,62141100,174
Lawley-Hotelling0,119721,61641080,175
Pillai0,109671,62541120,173
Roy0,10400       
s = 2    m = -0,5    n = 26,5

MANOVA-Tests für Methode*Werk




DF
KriteriumTeststatistikFZählerNennerp
Wilks0,858262,18441100,075
Lawley-Hotelling0,164392,21941080,072
Pillai0,142392,14641120,080
Roy0,15966       
s = 2    m = -0,5    n = 26,5
Wichtigste Ergebnisse: p

Die p-Werte für die Produktionsmethode sind auf dem Signifikanzniveau 0,10 statistisch signifikant. Die p-Werte für das Herstellungswerk sind auf dem Signifikanzniveau 0,10 bei keinem der Tests signifikant. Die p-Werte für die Wechselwirkung zwischen Werk und Methode sind auf dem Signifikanzniveau 0,10 statistisch signifikant. Da die Wechselwirkung statistisch signifikant ist, hängt der Effekt der Methode vom Werk ab.

Schritt 2: Bestimmen, welche Mittelwerte der Antwortvariablen für jeden Faktor die größten Differenzen aufweisen

Verwenden Sie die Eigenwertanalyse, um zu untersuchen, wie sich die Mittelwerte der Antwortvariablen zwischen den Stufen der verschiedenen Modellterme unterscheiden. Sie sollten sich dabei auf die Eigenvektoren konzentrieren, die hohen Eigenwerten entsprechen. Um die Eigenwertanalyse abzurufen, öffnen Sie Statistik > Varianzanalyse (ANOVA) > Allgemeine MANOVA > Ergebnisse, und wählen Sie die Option Eigenwertanalyse unter Darstellung der Ergebnisse aus.

Eigenwertanalyse für Methode

Eigenwert0,58480,00000
Anteil1,00000,00000
Kumulativ1,00001,00000
Eigenvektor12
Tauglichkeitsbewertung0,144062-0,07870
Qualitätsbewertung-0,0039680,13976
Wichtigste Ergebnisse: Eigenwert, Eigenvektor

In diesen Ergebnissen ist der erste Eigenwert für Methode (0,5848) größer als der zweite Eigenwert (0,00000). Somit sollten Sie dem ersten Eigenvektor eine größere Wichtigkeit beimessen. Der erste Eigenvektor für den Faktor Methode ist 0,144062; -0,003968. Der höchste Absolutwert innerhalb dieses Vektors bezieht sich auf die Tauglichkeitseinstufung. Dies legt nahe, dass die Mittelwerte für die Tauglichkeit die größte Differenz zwischen den Faktorstufen für die Methode aufweisen. Diese Informationen sind hilfreich beim Auswerten der Mittelwerttabelle.

Schritt 3: Auswerten der Differenzen zwischen Gruppenmittelwerten

Verwenden Sie die Mittelwerttabelle, um die statistisch signifikanten Differenzen zwischen den Faktorstufen in den Daten zu ermitteln. Der Mittelwert jeder Gruppe ist ein Schätzwert für den Mittelwert der Grundgesamtheit. Suchen Sie nach Differenzen zwischen Gruppenmittelwerten für Terme, die statistisch signifikant sind.

Für die Haupteffekte werden die Gruppen innerhalb der einzelnen Faktoren und die entsprechenden Mittelwerte in der Tabelle angezeigt. Für die Wechselwirkungseffekte werden alle möglichen Kombinationen der Gruppen in der Tabelle angezeigt. Wenn ein Wechselwirkungsterm statistisch signifikant ist, interpretieren Sie die Haupteffekte nur unter Berücksichtigung der Wechselwirkungseffekte.

Um die Mittelwerte anzuzeigen, öffnen Sie Statistik > Varianzanalyse (ANOVA) > Allgemeine MANOVA > Ergebnisse, wählen Sie Univariate Varianzanalyse aus, und geben Sie im Feld Den Termen entsprechende mittlere kleinste Quadrate anzeigen die Terme ein.

Mittlere kleinste Quadrate für Antworten


TauglichkeitsbewertungQualitätsbewertung

MittelwertSE des
Mittelwerts		MittelwertSE des
Mittelwerts



Methode       
  Methode 14,8190,1655,2420,193
  Methode 26,2120,1796,0260,211
Werk       
  Werk A5,7080,1925,8330,226
  Werk B5,4930,2325,9140,273
  Werk C5,3450,2065,1550,242
Methode*Werk       
  Methode 1 Werk A4,6670,2725,4170,319
  Methode 1 Werk B4,7000,2985,4000,350
  Methode 1 Werk C5,0910,2844,9090,334
  Methode 2 Werk A6,7500,2726,2500,319
  Methode 2 Werk B6,2860,3566,4290,418
  Methode 2 Werk C5,6000,2985,4000,350
Wichtigstes Ergebnis: Mittelwert

In diesen Ergebnissen wird in der Mittelwerttabelle veranschaulicht, wie die mittleren Tauglichkeits- und Qualitätseinstufungen in Abhängigkeit von Methode, Werk und der Wechselwirkung Methode*Werk variieren. Methode und der Wechselwirkungsterm sind auf dem Signifikanzniveau 0,10 statistisch signifikant. In der Tabelle wird ersichtlich, dass Methode 1 und Methode 2 mit einer mittleren Tauglichkeitseinstufung von 4,819 bzw. 6,212 verbunden sind. Die Differenzen zwischen diesen Mittelwerten ist größer als die Differenz zwischen den entsprechenden Mittelwerten für die Qualitätseinstufung. Dies bestätigt die Interpretation der Eigenwertanalyse.

Da der Wechselwirkungsterm Methode*Werk jedoch ebenfalls statistisch signifikant ist, können Sie die Haupteffekte nur unter Berücksichtigung der Wechselwirkungseffekte interpretieren. In der Tabelle für den Wechselwirkungsterm wird beispielsweise ersichtlich, dass Werk C bei Methode 1 mit der höchsten Tauglichkeitseinstufung und der niedrigsten Qualitätseinstufung verbunden ist. Bei Methode 2 ist jedoch Werk A mit der höchsten Tauglichkeitseinstufung und einer Qualitätseinstufung verbunden, die annähernd der höchsten Qualitätseinstufung entspricht.

Schritt 4: Auswerten der univariaten Ergebnisse, um einzelne Antwortvariablen zu untersuchen

Wenn Sie Allgemeine MANOVA durchführen, können Sie die univariaten Statistiken berechnen lassen, um die einzelnen Antwortvariablen zu untersuchen. Die univariaten Ergebnissen können ein intuitiveres Verständnis der Beziehungen in Ihren Daten vermitteln. Die univariaten Ergebnisse können sich jedoch von den multivariaten Ergebnissen unterscheiden.

Um die univariaten Ergebnisse anzuzeigen, öffnen Sie Statistik > Varianzanalyse (ANOVA) > Allgemeine MANOVA > Ergebnisse, und wählen Sie die Option Univariate Varianzanalyse unter Darstellung der Ergebnisse aus.

Um zu bestimmen, ob die Assoziation zwischen der Antwortvariablen und jedem Term im Modell statistisch signifikant ist, vergleichen Sie den p-Wert für den Term mit dem Signifikanzniveau, um die Nullhypothese auszuwerten. Die Nullhypothese besagt, dass keine Assoziation zwischen dem Term und der Antwortvariablen besteht. In der Regel ist ein Signifikanzniveau (als α oder Alpha bezeichnet) von 0,05 gut geeignet. Ein Signifikanzniveau von 0,05 bedeutet ein Risiko, dass auf eine vorhandene Assoziation geschlossen wird, während tatsächlich keine vorhanden ist, von 5 %.
p-Wert ≤ α: Die Assoziation ist statistisch signifikant
Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, können Sie schlussfolgern, dass eine statistisch signifikante Assoziation zwischen der Antwortvariablen und dem Term besteht.
p-Wert > α: Die Assoziation ist statistisch nicht signifikant
Wenn der p-Wert größer als das Signifikanzniveau ist, können Sie nicht schlussfolgern, dass eine statistisch signifikante Assoziation zwischen der Antwortvariablen und dem Term besteht. Es empfiehlt sich möglicherweise, dass Modell ohne den Term erneut anzupassen.
Wenn mehrere Prädiktoren ohne eine statistisch signifikante Assoziation mit der Antwortvariablen vorhanden sind, können Sie das Modell reduzieren, indem Sie Terme einzeln nacheinander entfernen. Weitere Informationen zum Entfernen von Termen aus dem Modell finden Sie unter Modellreduzierung.
Wenn ein Modellterm statistisch signifikant ist, hängt die Interpretation von der Art des Terms ab. Die Interpretationen lauten wie folgt:
  • Wenn ein kategorialer Faktor signifikant ist, können Sie schlussfolgern, dass nicht alle Mittelwerte der Faktorstufen gleich sind.
  • Wenn ein Wechselwirkungsterm signifikant ist, hängt die Beziehung zwischen einem Faktor und der Antwortvariablen von den anderen Faktoren im Term ab. In diesem Fall sollten Sie die Haupteffekte nicht interpretieren, ohne dabei den Wechselwirkungseffekt zu berücksichtigen.
  • Wenn eine Kovariate statistisch signifikant ist, können Sie schlussfolgern, dass eine Assoziation zwischen Änderungen des Werts der Kovariate und Änderungen des Mittelwerts der Antwortvariablen besteht.
  • Wenn ein Polynomialterm statistisch signifikant ist, können Sie schlussfolgern, dass die Daten eine Krümmung aufweisen.

Varianzanalyse für Tauglichkeitsbewertung unter Verwendung von korrigierter SS für Tests

QuelleDFSeq SSKor SSKor MSFp
  Methode131,26429,07429,073832,720,000
  Werk21,3661,4990,74950,840,436
  Methode*Werk27,0997,0993,54943,990,024
Fehler5649,75449,7540,8885   
Gesamt6189,484       

Varianzanalyse für Qualitätsbewertung unter Verwendung von korrigierter SS für Tests

QuelleDFSeq SSKor SSKor MSFp
  Methode18,85879,21969,21967,530,008
  Werk26,76327,05723,52862,880,064
  Methode*Werk20,70740,70740,35370,290,750
Fehler5668,590068,59001,2248   
Gesamt6184,9194       
Wichtigste Ergebnisse: p

In diesen Ergebnissen sind der p-Wert für den Haupteffekt von „Methode“ und den Wechselwirkungseffekt „Methode*Werk“ im Modell für die Tauglichkeitseinstufung auf dem Niveau 0,10 statistisch signifikant. Die Haupteffekte von „Methode“ und „Werk“ sind im Modell für die Qualitätseinstufung statistisch signifikant. Sie können schlussfolgern, dass zwischen Änderungen dieser Variablen und Änderungen der Antwortvariablen eine Assoziation besteht.

Schritt 5: Bestimmen, ob das Modell die Annahmen der Analyse erfüllt

Verwenden Sie die Residuendiagramme, um zu ermitteln, ob das Modell angemessen ist und die Annahmen der Analyse erfüllt. Wenn die Annahmen nicht erfüllt werden, ist das Modell u. U. nicht gut an die Daten angepasst, und Sie sollten beim Interpretieren der Ergebnisse vorsichtig sein.

Wenn Sie Allgemeine MANOVA ausführen, zeigt Minitab Residuendiagramme für alle im Modell enthaltenen Antwortvariablen an. Sie müssen feststellen, ob die Residuendiagramme für alle Antwortvariablen darauf hinweisen, dass das Modell die Annahmen erfüllt.

Weitere Informationen zum Umgang mit Mustern in den Residuendiagrammen finden Sie unter Residuendiagramme für Allgemeine MANOVA; klicken Sie dort auf den Namen des Residuendiagramms in der Liste am oberen Rand der Seite.

Diagramm der Residuen im Vergleich zu den Anpassungen

Verwenden Sie das Diagramm der Residuen im Vergleich zu den Anpassungen, um die Annahme zu überprüfen, dass die Residuen zufällig verteilt sind und eine konstante Varianz aufweisen. Im Idealfall sollten die Punkte zufällig auf beiden Seiten von null verteilt sein, und es sollten keine Muster in den Punkten erkennbar sein.

Die Muster in der folgenden Tabelle können darauf hinweisen, dass das Modell die Modellannahmen nicht erfüllt.
Muster Mögliche Bedeutung des Musters
Aufgefächerte oder ungleichmäßig gestreute Residuen für die angepassten Werte Nicht konstante Varianz
Krümmung Ein fehlender Term höherer Ordnung
Ein weit von null entfernt liegender Punkt Ein Ausreißer
Ein in x-Richtung weit von den anderen Punkten entfernter Punkt Ein einflussreicher Punkt
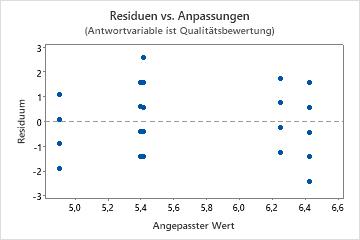
In diesem Diagramm der Residuen im Vergleich zu den Anpassungen scheinen die Daten zufällig um null gestreut zu sein. Es liegen keine Anzeichen dafür vor, dass der Wert des Residuums vom angepassten Wert abhängt.

Diagramm der Residuen im Vergleich zur Reihenfolge

Verwenden Sie das Diagramm der Residuen im Vergleich zur Reihenfolge, um die Annahme zu überprüfen, dass die Residuen zufällig verteilt sind. Bei in chronologischer Reihenfolge angezeigten unabhängigen Residuen sind weder Trends noch Muster zu erkennen. Muster in den Punkten können darauf hinweisen, dass nahe beieinander liegende Residuen korrelieren und daher nicht unabhängig sind. Im Idealfall sollten die Residuen im Diagramm zufällig um die Mittellinie gestreut sein:
Wenn Sie ein Muster erkennen, untersuchen Sie die Ursache. Die folgenden Typen von Mustern können darauf hinweisen, dass die Residuen abhängig sind.
Trend
Shift
Zyklus
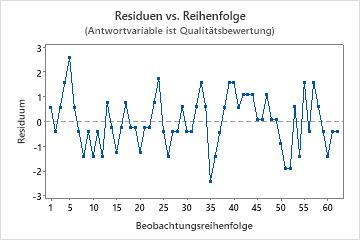
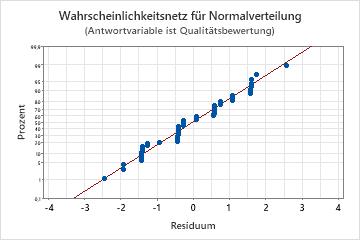
In diesem Diagramm der Residuen im Vergleich zur Reihenfolge scheinen die Residuen zufällig um die Mittellinie gestreut zu sein. Es liegen keine Anzeichen dafür vor, dass die Residuen nicht unabhängig sind.

Wahrscheinlichkeitsnetz (Normal) für Residuen

Verwenden Sie das Wahrscheinlichkeitsnetz (Normal) der Residuen, um die Annahme zu überprüfen, dass die Residuen normalverteilt sind. Die Residuen im Wahrscheinlichkeitsnetz für Normalverteilung sollten ungefähr einer Geraden folgen.

Die Muster in der folgenden Tabelle können darauf hinweisen, dass das Modell die Modellannahmen nicht erfüllt.
Muster Mögliche Bedeutung des Musters
Keine Gerade Nicht-Normalverteilung
Ein Punkt weit entfernt von der Linie Ein Ausreißer
Unbeständige Steigung Eine nicht identifizierte Variable
In diesem Wahrscheinlichkeitsnetz (Normal) für Residuen scheinen die Punkte durchgängig einer Geraden zu folgen. Es liegen keine Anzeichen für Nicht-Normalverteilung, Ausreißer oder nicht identifizierte Variablen vor.
Copyright © 2024 Minitab, LLC. All rights Reserved.