In diesem Thema
GLM-Modell
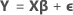
Notation
| Begriff | Beschreibung |
|---|---|
| Y | Vektor der Werte der Antwortvariablen |
| X | Designmatrix |
| β | Vektor der Parameter |
| ε | Vektor der unabhängigen normalverteilten Zufallsvariablen |
Designmatrix
Das allgemeine lineare Modell passt das angegebene Modell mit Hilfe eines Regressionsverfahrens an. Zunächst erstellt Minitab auf der Grundlage der Faktoren und Kovariaten sowie des angegebenen Modells eine Designmatrix. Die Spalten dieser Matrix stellen die Prädiktoren für die Regression dar.
Die Designmatrix umfasst n Zeilen, wobei n die Anzahl der Beobachtungen ist, sowie mehrere Blöcke von Spalten, die den Termen im Modell entsprechen. Der erste Block steht für die Konstante und enthält lediglich eine Spalte, die nur Einsen enthält. Der Block für eine Kovariate enthält ebenfalls nur eine Spalte, die Kovariatenspalte selbst. Der Block von Spalten für einen Faktor enthält r Spalten, wobei r die Freiheitsgrade für den Faktor angibt, und sie sind wie im nachfolgenden Beispiel kodiert.
Angenommen, A ist ein Faktor mit 4 Stufen. Der Faktor verfügt folglich über 3 Freiheitsgrade, und sein Block enthält 3 Spalten (A1, A2, A3).
| Stufe von A | A1 | A2 | A3 |
|---|---|---|---|
| 1 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 |
| 4 | –1 | –1 | –1 |
Angenommen, Faktor B hat 3 Stufen, die in den einzelnen Stufen von A geschachtelt sind. Sein Block verfügt folglich über (3 – 1) x 4 = 8 Spalten (B11, B12, B21, B22, B31, B32, B41, B42), die wie folgt kodiert sind:
| Stufe von A | Stufe von B | B11 | B12 | B21 | B22 | B31 | B32 | B41 | B42 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 3 | –1 | –1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 2 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 2 | 3 | 0 | 0 | –1 | –1 | 0 | 0 | 0 | 0 |
| 3 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 3 | 2 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 3 | 3 | 0 | 0 | 0 | 0 | –1 | –1 | 0 | 0 |
| 4 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 4 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 4 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | –1 | –1 |
Um die Spalten für einen Wechselwirkungsterm zu berechnen, multiplizieren Sie einfach alle entsprechenden Spalten für die Faktoren und/oder Kovariaten in der Wechselwirkung. Angenommen, Faktor A weist 6 Stufen auf, C hat 3 Stufen, D verfügt über 4 Stufen, und Z und W stellen Kovariaten dar. Term A * C * D * Z * W * W weist dann 5 x 2 x 3 x 1 x 1 x 1 = 30 Spalten auf. Um diese zu bestimmen, multiplizieren Sie jede Spalte für A mit jeder für C, mit jeder für D sowie einmal mit der Kovariaten Z und zweimal mit der Kovariaten W.
Box-Cox-Transformation
Bei der Box-Cox-Transformation werden Lambda-Werte (siehe unten) ausgewählt, die die Summe der Quadrate der Residuen minimieren. Die resultierende Transformation ist Y λ, wenn λ ≠ 0, und ln(Y), wenn λ = 0. Wenn λ < 0, multipliziert Minitab zudem die transformierte Antwortvariable mit −1, um die Reihenfolge aus der nicht transformierten Antwortvariablen beizubehalten.
Minitab sucht einen optimalen Wert zwischen −2 und 2. Werte, die außerhalb dieses Intervalls liegen, führen möglicherweise nicht zu einer besseren Anpassung.
Hier finden Sie einige der gängigsten Transformationen, wobei Y′ das transformierte Y der Daten darstellt:
| Lambda-Wert (λ) | Transformation |
|---|---|
| λ = 2 | Y′ = Y 2 |
| λ = 0,5 | Y′ = 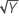 |
| λ = 0 | Y′ = ln(Y ) |
| λ = −0,5 |  |
| λ = −1 | Y′ = −1 / Y |
Gewichtete Regression
Bei der Regression der gewichteten kleinsten Quadrate handelt es sich um eine Methode zum Behandeln von Beobachtungen, deren Varianzen nicht konstant sind. Wenn die Varianzen nicht konstant sind, gelten für die Beobachtungen folgende Hinweise:
- Großen Varianzen sollten relativ kleine Gewichtungen zugewiesen werden.
- Kleinen Varianzen sollten relativ große Gewichtungen zugewiesen werden.
Üblicherweise wird für die Gewichtungen die Umkehrung der reinen Fehlervarianz in der Antwortvariablen ausgewählt.
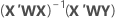
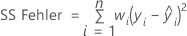
Notation
| Begriff | Beschreibung |
|---|---|
| X | Designmatrix |
| X' | transponierte Designmatrix |
| W | eine (n x n)-Matrix mit den Gewichtungen auf der Diagonalen |
| Y | Vektor von Werten der Antwortvariablen |
| n | Anzahl der Beobachtungen |
| wi | Gewichtung für die i-te Beobachtung |
| yi | Wert der Antwortvariablen für die i-te Beobachtung |
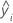 | angepasster Wert für die i-te Beobachtung |
So entfernt Minitab stark korrelierte Prädiktoren aus der Regressionsgleichung in Allgemeines lineares Modell anpassen
- Minitab führt eine QR-Zerlegung für die x-Matrix durch.
Hinweis
Das R2 kann mit Hilfe der QR-Zerlegung schneller als mit der Regression der kleinsten Quadrate berechnet werden.
- Minitab führt eine Regression eines Prädiktors auf alle anderen Prädiktoren durch und berechnet das R2. Wenn 1 – R2 < 4 * 2,22e-16, besteht der Prädiktor den Test nicht, und er wird aus dem Modell entfernt.
- Minitab wiederholt die Schritte 1 und 2 für die verbleibenden Prädiktoren.
Beispiel
- Minitab führt eine Regression von x5 auf x1-x4 aus. Wenn 1 – R2 größer als 4 * 2,22e-16 ist, verbleibt x5 in der Gleichung. Der Prädiktor x5 besteht den Test und verbleibt in der Gleichung.
- Minitab führt eine Regression von x4 auf x1, x2, x3 und x5 aus. Angenommen, 1 – R2 ist für diese Regression größer als 4 * 2,22e-16, und der Prädiktor wird somit in der Gleichung beibehalten.
- Minitab führt eine Regression von x3 auf x1, x2, x4 und x5 aus und berechnet das R2. Der Prädiktor x3 besteht den Test nicht und wird daher aus der Gleichung entfernt.
- Minitab nimmt eine erneute QR-Zerlegung für die x-Matrix vor und führt eine Regression von x2 auf die verbleibenden Prädiktoren x1, x4 und x5 durch. Der Prädiktor x2 besteht den Test.
- Minitab führt eine Regression von x1 auf x2, x4 und x5 aus. Der Prädiktor besteht den Test nicht und wird aus der Gleichung entfernt.
Minitab führt eine Regression von y auf x2, x4, x5 aus. Die Ergebnisse enthalten eine Meldung, die besagt, dass die Prädiktoren x1 und x3 nicht geschätzt werden können und aus dem Modell entfernt wurden.
Hinweis
Sie können den Unterbefehl TOLERANCE mit dem Sessionbefehl GLM verwenden, um zu erzwingen, dass Minitab einen Prädiktor im Modell beibehält, der stark mit einem anderen Prädiktor korreliert. Das Absenken der Toleranz ist jedoch nicht ohne Risiko, da so möglicherweise numerisch ungenaue Ergebnisse entstehen.
