In diesem Thema
- R-Qd(kor)
- Varianzkomponenten
- Erwartetes Mittel der Quadrate
- F-Statistik für Modelle mit Zufallsfaktoren
- So wird die F-Statistik in der ANOVA-Ausgabe berechnet
- Weshalb enthält die ANOVA-Ausgabe ein „x“ neben einem p-Wert in der ANOVA-Tabelle sowie die Beschriftung „Kein genauer F-Test“?
- Informationen zur Meldung „Nenner von F-Test ist null oder nicht definiert“
- Angepasster Wert
- Residuum (Resid)
Balanciertes ANOVA-Modell
Das balancierte ANOVA-Modell für drei oder mehr Faktoren stellt eine direkte Erweiterung eines Modells der zweifachen Varianzanalyse dar.
Ein balanciertes Drei-Faktor-ANOVA-Modell mit den Faktoren A, B und C lautet wie folgt:
yijkm = μ + α i+ β j + γ k + (αβ)ij+ (αγ)ik+ (βγ)jk+ (αβγ)ijk+εijkm
Wenn die Faktoren fest sind, gilt Σαi = 0, Σβj = 0, Σγk = 0, Σ(αβ)ij = 0, Σ(αγ)ik = 0, Σ(βγ)jk = 0, Σ(αβγ)ijk = 0 und εijkm sind unabhängig und gemäß N(0, σ2) verteilt.
Wenn die Faktoren zufällig sind, sind α i, β j , γk, (αβ)ij, (αγ)ik, (βγ)jk, (αβγ)ijk und εijkm unabhängige Zufallsvariablen. Die Variablen sind normalverteilt mit dem Mittelwert null und Varianzen, die angegeben werden durch V(αi) = σ2α, V(β j) = σ2β, V(γk) = σ2γ, V[(αβ)ij] = σ2αβ, V[(αγ)jk] = σ2αγ, V[(βγ)jk] = σ2βγ, V(εijkm) = σ2.
Das Drei-Faktor-Modell kann auf Modelle mit mehr als drei Faktoren erweitert werden.
Faktormittelwerte
Formel
Der Durchschnitt der Beobachtungen für einen Faktor auf einer bestimmten Stufe. Die Formeln lauten wie folgt:
Mittelwert von Faktor A: 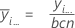
Mittelwert von Faktor B: 
Mittelwert von Faktor C: 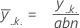
Gesamtmittelwert: 
Notation
| Begriff | Beschreibung |
|---|---|
| yi... | Summe aller Beobachtungen auf der i-ten Faktorstufe von A |
| y.j.. | Summe aller Beobachtungen auf der j-ten Faktorstufe von B |
| y..k. | Summe aller Beobachtungen auf der k-ten Faktorstufe von C |
| y.... | Summe aller Beobachtungen in der Stichprobe |
| a | Anzahl der Stufen in A |
| b | Anzahl der Stufen in B |
| c | Anzahl der Stufen in C |
| n | Anzahl der Beobachtungen in den einzelnen Kombinationen von Faktor und Stufen |
Summe der Quadrate (SS)
Die Summe der quadrierten Distanzen. SS Gesamt gibt die Gesamtstreuung der Daten an. SS (A), SS (B) und SS (C) stellen den Betrag der Streuung des geschätzten Mittelwerts der Faktorstufen um den Gesamtmittelwert dar. Gelegentlich werden diese auch als Summe der Quadrate zwischen Behandlungen bezeichnet. SS(AB), SS(AC), SS(BC) und SS(ABC) stellen den Betrag der Streuung dar, der vom jeweiligen Wechselwirkungsterm erklärt wird. SS Fehler stellt den Betrag der Streuung zwischen dem angepassten Wert und der tatsächlichen Beobachtung dar. Dies wird auch als Fehler innerhalb von Behandlungen bezeichnet. Bei diesen Formeln wird angenommen, dass ein vollständiges Modell angepasst wird. Die Berechnungen lauten wie folgt:

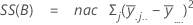

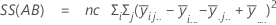
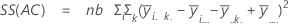
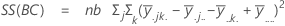
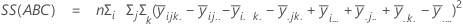
- SS Fehler = SS gesamt – SS (für alle Terme im Modell)
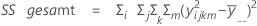
Notation
| Begriff | Beschreibung |
|---|---|
| a | Anzahl der Stufen in Faktor A |
| b | Anzahl der Stufen in Faktor B |
| c | Anzahl der Stufen in Faktor C |
| n | Gesamtzahl der Versuche |
 | Mittelwert der i-ten Faktorstufe von Faktor A |
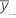 | Gesamtmittelwert aller Beobachtungen |
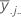 | Mittelwert der j-ten Faktorstufe von Faktor B |
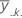 | Mittelwert der k-ten Faktorstufe von Faktor C |
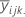 | geschätzter Behandlungsmittelwert |
Freiheitsgrade (DF)
Die Freiheitsgrade für jede Komponente des Modells werden wie folgt ausgedrückt:
| Quellen der Streuung | DF |
|---|---|
| Faktor | ki – 1 |
| Kovariaten und Wechselwirkungen zwischen Kovariaten | 1 |
| Wechselwirkungen, die Faktoren umfassen | 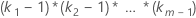 |
| Regression | p |
| Fehler | n – p – 1 |
| Gesamt | n – 1 |
Notation
| Begriff | Beschreibung |
|---|---|
| ki | Anzahl der Stufen im i-ten Faktor |
| m | Anzahl der Faktoren |
| n | Anzahl der Beobachtungen |
| p | Anzahl der Koeffizienten im Modell, wobei die Konstante nicht gezählt wird |
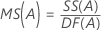
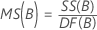
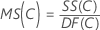
Mittel der Quadrate (MS)
Formeln
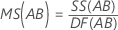
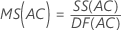
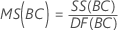
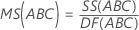

F
Für eine Drei-Faktor-ANOVA mit durchgängig festen Faktoren werden die F-Statistiken mit den folgenden Formeln ausgedrückt, wenn das Modell vollständig ist.
Formeln






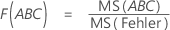
- Für F(A) sind die Freiheitsgrade für den Zähler gleich a – 1 und für den Nenner gleich (n – 1)abc.
- Für F(B) sind die Freiheitsgrade für den Zähler gleich b – 1 und für den Nenner gleich (n – 1)abc.
- Für F(C) sind die Freiheitsgrade für den Zähler gleich c – 1 und für den Nenner gleich (n – 1)abc.
- Für F(AB) sind die Freiheitsgrade für den Zähler gleich (a – 1)(b – 1) und für den Nenner gleich (n – 1)abc.
- Für F(AC) sind die Freiheitsgrade für den Zähler gleich (a – 1)(c – 1) und für den Nenner gleich (n – 1)abc.
- Für F(BC) sind die Freiheitsgrade für den Zähler gleich (b – 1)(c – 1) und für den Nenner gleich (n – 1)abc.
- Für F(ABC) sind die Freiheitsgrade für den Zähler gleich (a – 1)(b – 1)(c – 1) und für den Nenner gleich (n – 1)abc.
Wenn Zufallsfaktoren im Modell enthalten sind, wird das F-Verhältnis für jeden Term durch das erwartete Mittel der Quadrate für jeden Term bestimmt.
Größere Werte für F legen nahe, dass die Nullhypothese zurückgewiesen werden sollte. Sie können schlussfolgern, dass der Effekt statistisch signifikant ist.
p-Wert – Tabelle der Varianzanalyse
Der p-Wert ist ein Wahrscheinlichkeitsmaß, das aus einer F-Verteilung mit den Freiheitsgraden (DF) wie folgt berechnet wird:
- DF des Zählers
- Summe der Freiheitsgrade für den Term oder die Terme im Test
- DF des Nenners
- Freiheitsgrade für Fehler
Formel
1 − P(F ≤ fj)
Notation
| Begriff | Beschreibung |
|---|---|
| P(F ≤ f) | kumulative Verteilungsfunktion für die F-Verteilung |
| f | F-Statistik für den Test |
S

Notation
| Begriff | Beschreibung |
|---|---|
| MSE | Mittleres Fehlerquadrat |
R-Qd
R2 wird auch als Determinationskoeffizient bezeichnet.
Formel

Notation
| Begriff | Beschreibung |
|---|---|
| yi | i-ter beobachteter Wert der Antwortvariablen |
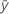 | Mittelwert der Antwortvariablen |
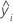 | i-ter angepasster Wert der Antwortvariablen |
R-Qd(kor)
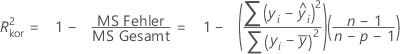
Obwohl die Berechnungen für das korrigierte R2 negative Werte ergeben können, zeigt Minitab in derartigen Fällen null an.
Notation
| Begriff | Beschreibung |
|---|---|
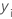 | i-ter beobachteter Wert der Antwortvariablen |
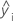 | i-ter angepasster Wert der Antwortvariablen |
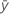 | Mittelwert der Antwortvariablen |
| n | Anzahl der Beobachtungen |
| p | Anzahl der Terme im Modell |
Varianzkomponenten
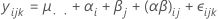
Hierbei sind αi, βj , (αβ)ij und εijk unabhängige Zufallsvariablen. Die Variablen sind normalverteilt mit dem Mittelwert null, und die Varianzen werden durch diese Formeln ausgedrückt:
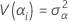

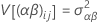

Bei diesen Varianzen handelt es sich um die Varianzkomponenten. Testen Sie in diesem Fall die Hypothese, dass die Varianzkomponenten gleich null sind.
Für ein eingeschränktes gemischtes Modell mit zwei Faktoren wird das Modell wie folgt ausgedrückt:
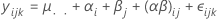
Hierbei ist αi ein fester Effekt, βj ist ein Zufallseffekt, (αβ)ij, ist ein Zufallseffekt, und εijk ist der Zufallsfehler. Σαi = 0 und Σ(αβ)ij = 0 für jedes j. Die Varianzen sind V(βj) = σ2β,V[(αβ)ij] =[(a–1)/a]σ2αβ und V(εijk) = σ2. σ2β, σ2αβ und σ2 sind Varianzkomponenten. Die Summierung der Wechselwirkungskomponente über den festen Faktor ergibt null, was darauf verweist, dass es sich um das eingeschränkte gemischte Modell handelt.
Für ein uneingeschränktes gemischtes Modell mit einem festen Faktor A und einem Zufallsfaktor B wird das Modell mit folgender Formel beschrieben:
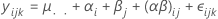
Hierbei sind αi feste Effekte und βj, (αβ)ij sowie εijk nicht korrelierte Zufallsvariablen mit dem Mittelwert null und den folgenden Varianzen:

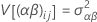

Bei diesen Varianzen handelt es sich um die Varianzkomponenten. Σα i = 0 und Σ(αβ)ij = 0 für jedes j.
Diese Informationen beziehen sich auf balancierte Modelle. Informationen zu nicht balancierten bzw. komplexeren Modellen finden Sie in Montgomery1 und Neter2.
- D. C. Montgomery (1991). Design and Analysis of Experiments, Third Edition. John Wiley & Sons.
- J. Neter, W. Wasserman und M. H. Kutner (1985). Applied Linear Statistical Models, Second Edition. Irwin, Inc.
Erwartetes Mittel der Quadrate
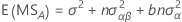



Die Formeln für das erwartete Mittel der Quadrate für ein eingeschränktes gemischtes Modell mit den zwei Faktoren A (fest) und B (zufällig) lauten wie folgt:
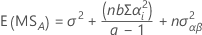



Die Formeln für das erwartete Mittel der Quadrate für ein uneingeschränktes gemischtes Modell mit einem festen Faktor A und einem Zufallsfaktor B lauten wie folgt:
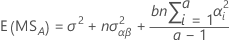



Die allgemeinen Regeln zum Berechnen des erwarteten Mittels der Quadrate und Informationen zu nicht balancierten bzw. komplexeren Modellen finden Sie in Montgomery1 und Neter2.
- D. C. Montgomery (1991). Design and Analysis of Experiments, Third Edition. John Wiley & Sons.
- J. Neter, W. Wasserman und M. H. Kutner (1985). Applied Linear Statistical Models, Second Edition. Irwin, Inc.
Notation
| Begriff | Beschreibung |
|---|---|
| b | Anzahl der Stufen in Faktor B |
| a | Anzahl der Stufen in Faktor A |
| n | Anzahl der Beobachtungen |
| σ2 | geschätzte Varianz des Modells |
 | geschätzte Varianz von A |
 | geschätzte Varianz von B |
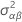 | geschätzte Varianz von AB |
 | feste Effekte von A |
F-Statistik für Modelle mit Zufallsfaktoren
So wird die F-Statistik in der ANOVA-Ausgabe berechnet
Jede F-Statistik stellt ein Verhältnis von Mitteln der Quadrate dar. Der Zähler ist das Mittel der Quadrate für den Term. Der Nenner wird so gewählt, dass sich der erwartete Wert des Mittels der Quadrate im Zähler vom erwarteten Wert des Mittels der Quadrate im Nenner nur durch den relevanten Effekt unterscheidet. Der Effekt für einen Zufallsterm wird durch die Varianzkomponente des Terms dargestellt. Der Effekt für einen festen Term wird durch die Summe der Quadrate der diesem Term entsprechenden Modellkomponenten dividiert durch seine Freiheitsgrade dargestellt. Daher weist eine hohe F-Statistik auf einen signifikanten Effekt hin.
Wenn alle Terme im Modell fest sind, ist der Nenner für jede F-Statistik das mittlere Fehlerquadrat (MSE). Für Modelle, die Zufallsterme enthalten, ist MSE hingegen nicht immer das richtige Mittel der Quadrate. Anhand des erwarteten Mittels der Quadrate (EMS) kann bestimmt werden, welches für den Nenner geeignet ist.
Beispiel
| Quelle | Erwartetes Mittel der Quadrate für jeden Term |
|---|---|
| (1) Bildschirm | (4) + 2,0000(3) + Q[1] |
| (2) Techniker | (4) + 2,0000(3) + 4,0000(2) |
| (3) Bildschirm*Techniker | (4) + 2,0000(3) |
| (4) Fehler | (4) |
Eine Zahl in Klammern gibt einen Zufallseffekt an, der dem neben der Quellennummer aufgelisteten Term zugeordnet ist. (2) stellt den Zufallseffekt von „Techniker“ dar, (3) den Zufallseffekt der Wechselwirkung „Bildschirm*Techniker“ und (4) den Zufallseffekt von „Fehler“. Das EMS für „Fehler“ ist der Effekt des Fehlerterms. Zudem ist das EMS für „Bildschirm*Techniker“ der Effekt des Fehlerterms zuzüglich des doppelten Effekts der Wechselwirkung „Bildschirm*Techniker“.
Zum Berechnen der F-Statistik für „Folie*Tech“ wird das Mittel der Quadrate für „Folie*Tech“ durch das Mittel der Quadrate des Fehlers dividiert, sodass sich der erwartete Wert des Zählers (EMS für Folie*Tech = (4) + 2.0000(3)) vom erwarteten Wert des Nenners (EMS für Fehler = (4)) nur durch den Effekt der Wechselwirkung (2,0000(3)) unterscheidet. Daher zeigt eine hohe F-Statistik eine signifikante Wechselwirkung „Bildschirm*Techniker“ an.
Eine Zahl mit Q[ ] gibt den festen Effekt für den Term an, der neben der Quellennummer aufgelistet ist. So ist Q[1] beispielsweise der feste Effekt von „Bildschirm“. Das EMS für „Bildschirm“ ist der Effekt des Fehlerterms zuzüglich des doppelten Effekts der Wechselwirkung „Bildschirm*Techniker“ plus ein konstantes Vielfaches des Effekts von „Bildschirm“. Q[1] ist gleich (b*n * sum((Koeffizienten für Stufen von „Bildschirm“)**2)) dividiert durch (a – 1), wobei a und b die Anzahl der Stufen von „Bildschirm“ und „Techniker“ sind und n die Anzahl der Replikationen angibt.
Zum Berechnen der F-Statistik für „Bildschirm“ wird das Mittel der Quadrate für „Bildschirm“ durch das Mittel der Quadrate für „Bildschirm*Techniker“ dividiert, so dass sich der erwartete Wert des Zählers (EMS für „Bildschirm“ = (4) + 2,0000(3) + Q[1]) vom erwarteten Wert des Nenners (EMS für „Bildschirm*Techniker“ = (4) + 2,0000(3)) nur durch den Effekt von „Bildschirm“ (Q[1]) unterscheidet. Daher weist eine hohe F-Statistik auf einen signifikanten Effekt von „Bildschirm“ hin.
Weshalb enthält die ANOVA-Ausgabe ein „x“ neben einem p-Wert in der ANOVA-Tabelle sowie die Beschriftung „Kein genauer F-Test“?
In einem genauen F-Test für einen Term unterscheidet sich der erwartete Wert des Mittels der Quadrate für den Zähler vom erwarteten Wert des Mittels der Quadrate für den Nenner nur durch die Varianzkomponente bzw. den festen Faktor von Interesse.
Gelegentlich kann ein solches Mittel der Quadrate jedoch nicht berechnet werden. In einem solchen Fall verwendet Minitab ein Mittel der Quadrate, das zu einem annähernden F-Test führt, und zeigt ein „x“ neben dem p-Wert an, um anzugeben, dass der F-Test nicht genau ist.
| Quelle | Erwartetes Mittel der Quadrate für jeden Term |
|---|---|
| (1) Zusatz | (4) + 1,7500(3) + Q[1] |
| (2) See | (4) + 1,7143(3) + 5,1429(2) |
| (3) Zusatz*See | (4) + 1,7500(3) |
| (4) Fehler | (4) |
Die F-Statistik für „Zusatz“ ist das Mittel der Quadrate für „Zusatz“ dividiert durch das Mittel der Quadrate für die Wechselwirkung „Zusatz*See“. Wenn der Effekt für „Zusatz“ sehr klein ist, ist der erwartete Wert des Zählers gleich dem erwarteten Wert des Nenners. Dies ist ein Beispiel für einen genauen F-Test.
Beachten Sie jedoch, dass für einen sehr kleinen Effekt von „See“ kein Mittel der Quadrate vorliegt, bei dem der erwartete Wert des Zählers gleich dem erwarteten Wert des Nenners ist. Daher verwendet Minitab einen annähernden F-Test. In diesem Beispiel wird das Mittel der Quadrate für „See“ durch das Mittel der Quadrate für die Wechselwirkung „Zusatz*See“ dividiert. Dadurch wird ein erwarteter Wert des Zählers erhalten, der annähernd gleich dem des Nenners ist, wenn der Effekt von „See“ sehr klein ist.
Informationen zur Meldung „Nenner von F-Test ist null oder nicht definiert“
- Für den Fehler ist nicht mindestens ein Freiheitsgrad vorhanden.
-
Die korrigierten MS-Werte sind sehr klein, und damit ist keine ausreichende Genauigkeit zur Anzeige der F-Statistik und der p-Werte gegeben. Mögliche Problemumgehung: Multiplizieren Sie die Antwortspalte mit 10. Führen Sie anschließend dasselbe Regressionsmodell aus, wobei Sie jedoch diese neue Antwortspalte als Antwortvariable verwenden.
Hinweis
Das Multiplizieren der Werte der Antwortvariablen mit 10 wirkt sich nicht auf die F-Statistik und die p-Werte aus, die Minitab in der Ausgabe anzeigt. Die Position des Dezimalkommas in der übrigen Ausgabe ist jedoch betroffen, insbesondere die Spalten für die sequenzielle Summe der Quadrate, Kor SS, Kor MS, Anpassung, Standardfehler der Anpassungen und Residuen.
So wird die F-Statistik in der ANOVA-Ausgabe berechnet
Jede F-Statistik stellt ein Verhältnis von Mitteln der Quadrate dar. Der Zähler ist das Mittel der Quadrate für den Term. Der Nenner wird so gewählt, dass sich der erwartete Wert des Mittels der Quadrate im Zähler vom erwarteten Wert des Mittels der Quadrate im Nenner nur durch den relevanten Effekt unterscheidet. Der Effekt für einen Zufallsterm wird durch die Varianzkomponente des Terms dargestellt. Der Effekt für einen festen Term wird durch die Summe der Quadrate der diesem Term entsprechenden Modellkomponenten dividiert durch seine Freiheitsgrade dargestellt. Daher weist eine hohe F-Statistik auf einen signifikanten Effekt hin.
Wenn alle Terme im Modell fest sind, ist der Nenner für jede F-Statistik das mittlere Fehlerquadrat (MSE). Für Modelle, die Zufallsterme enthalten, ist MSE hingegen nicht immer das richtige Mittel der Quadrate. Anhand des erwarteten Mittels der Quadrate (EMS) kann bestimmt werden, welches für den Nenner geeignet ist.
Beispiel
| Quelle | Erwartetes Mittel der Quadrate für jeden Term |
|---|---|
| (1) Bildschirm | (4) + 2,0000(3) + Q[1] |
| (2) Techniker | (4) + 2,0000(3) + 4,0000(2) |
| (3) Bildschirm*Techniker | (4) + 2,0000(3) |
| (4) Fehler | (4) |
Eine Zahl in Klammern gibt einen Zufallseffekt an, der dem neben der Quellennummer aufgelisteten Term zugeordnet ist. (2) stellt den Zufallseffekt von „Techniker“ dar, (3) den Zufallseffekt der Wechselwirkung „Bildschirm*Techniker“ und (4) den Zufallseffekt von „Fehler“. Das EMS für „Fehler“ ist der Effekt des Fehlerterms. Zudem ist das EMS für „Bildschirm*Techniker“ der Effekt des Fehlerterms zuzüglich des doppelten Effekts der Wechselwirkung „Bildschirm*Techniker“.
Zum Berechnen der F-Statistik für „Folie*Tech“ wird das Mittel der Quadrate für „Folie*Tech“ durch das Mittel der Quadrate des Fehlers dividiert, sodass sich der erwartete Wert des Zählers (EMS für Folie*Tech = (4) + 2.0000(3)) vom erwarteten Wert des Nenners (EMS für Fehler = (4)) nur durch den Effekt der Wechselwirkung (2,0000(3)) unterscheidet. Daher zeigt eine hohe F-Statistik eine signifikante Wechselwirkung „Bildschirm*Techniker“ an.
Eine Zahl mit Q[ ] gibt den festen Effekt für den Term an, der neben der Quellennummer aufgelistet ist. So ist Q[1] beispielsweise der feste Effekt von „Bildschirm“. Das EMS für „Bildschirm“ ist der Effekt des Fehlerterms zuzüglich des doppelten Effekts der Wechselwirkung „Bildschirm*Techniker“ plus ein konstantes Vielfaches des Effekts von „Bildschirm“. Q[1] ist gleich (b*n * sum((Koeffizienten für Stufen von „Bildschirm“)**2)) dividiert durch (a – 1), wobei a und b die Anzahl der Stufen von „Bildschirm“ und „Techniker“ sind und n die Anzahl der Replikationen angibt.
Zum Berechnen der F-Statistik für „Bildschirm“ wird das Mittel der Quadrate für „Bildschirm“ durch das Mittel der Quadrate für „Bildschirm*Techniker“ dividiert, so dass sich der erwartete Wert des Zählers (EMS für „Bildschirm“ = (4) + 2,0000(3) + Q[1]) vom erwarteten Wert des Nenners (EMS für „Bildschirm*Techniker“ = (4) + 2,0000(3)) nur durch den Effekt von „Bildschirm“ (Q[1]) unterscheidet. Daher weist eine hohe F-Statistik auf einen signifikanten Effekt von „Bildschirm“ hin.
Weshalb enthält die ANOVA-Ausgabe ein „x“ neben einem p-Wert in der ANOVA-Tabelle sowie die Beschriftung „Kein genauer F-Test“?
In einem genauen F-Test für einen Term unterscheidet sich der erwartete Wert des Mittels der Quadrate für den Zähler vom erwarteten Wert des Mittels der Quadrate für den Nenner nur durch die Varianzkomponente bzw. den festen Faktor von Interesse.
Gelegentlich kann ein solches Mittel der Quadrate jedoch nicht berechnet werden. In einem solchen Fall verwendet Minitab ein Mittel der Quadrate, das zu einem annähernden F-Test führt, und zeigt ein „x“ neben dem p-Wert an, um anzugeben, dass der F-Test nicht genau ist.
| Quelle | Erwartetes Mittel der Quadrate für jeden Term |
|---|---|
| (1) Zusatz | (4) + 1,7500(3) + Q[1] |
| (2) See | (4) + 1,7143(3) + 5,1429(2) |
| (3) Zusatz*See | (4) + 1,7500(3) |
| (4) Fehler | (4) |
Die F-Statistik für „Zusatz“ ist das Mittel der Quadrate für „Zusatz“ dividiert durch das Mittel der Quadrate für die Wechselwirkung „Zusatz*See“. Wenn der Effekt für „Zusatz“ sehr klein ist, ist der erwartete Wert des Zählers gleich dem erwarteten Wert des Nenners. Dies ist ein Beispiel für einen genauen F-Test.
Beachten Sie jedoch, dass für einen sehr kleinen Effekt von „See“ kein Mittel der Quadrate vorliegt, bei dem der erwartete Wert des Zählers gleich dem erwarteten Wert des Nenners ist. Daher verwendet Minitab einen annähernden F-Test. In diesem Beispiel wird das Mittel der Quadrate für „See“ durch das Mittel der Quadrate für die Wechselwirkung „Zusatz*See“ dividiert. Dadurch wird ein erwarteter Wert des Zählers erhalten, der annähernd gleich dem des Nenners ist, wenn der Effekt von „See“ sehr klein ist.
Informationen zur Meldung „Nenner von F-Test ist null oder nicht definiert“
- Für den Fehler ist nicht mindestens ein Freiheitsgrad vorhanden.
-
Die korrigierten MS-Werte sind sehr klein, und damit ist keine ausreichende Genauigkeit zur Anzeige der F-Statistik und der p-Werte gegeben. Mögliche Problemumgehung: Multiplizieren Sie die Antwortspalte mit 10. Führen Sie anschließend dasselbe Regressionsmodell aus, wobei Sie jedoch diese neue Antwortspalte als Antwortvariable verwenden.
Hinweis
Das Multiplizieren der Werte der Antwortvariablen mit 10 wirkt sich nicht auf die F-Statistik und die p-Werte aus, die Minitab in der Ausgabe anzeigt. Die Position des Dezimalkommas in der übrigen Ausgabe ist jedoch betroffen, insbesondere die Spalten für die sequenzielle Summe der Quadrate, Kor SS, Kor MS, Anpassung, Standardfehler der Anpassungen und Residuen.
Angepasster Wert
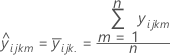
Notation
Für ein Drei-Faktor-Modell:
| Begriff | Beschreibung |
|---|---|
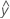 | angepasster Wert für die Beobachtung auf der i-ten Stufe von Faktor A, der j-ten Stufe von Faktor B, der k-ten Stufe von Faktor C |
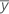 | Mittelwert für die Beobachtung auf der i-ten Stufe von Faktor A, der j-ten Stufe von Faktor B, der k-ten Stufe von Faktor C |
| n | Anzahl der Beobachtungen auf der i-ten Stufe von Faktor A, der j-ten Stufe von Faktor B, der k-ten Stufe von Faktor C |
Residuum (Resid)
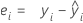
Notation
| Begriff | Beschreibung |
|---|---|
| ei | i-tes Residuum |
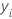 | i-ter beobachteter Wert der Antwortvariablen |
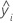 | i-ter angepasster Wert der Antwortvariablen |
