In diesem Thema
Methode
Für zweifaktorielle Modelle stellt die Mittelwertanalyse ein Verfahren dar, mit dem ermittelt wird, ob die Wechselwirkungseffekte signifikant sind oder sich die Haupteffekte vom Gesamtmittel unterscheiden. Bei der zweifachen Mittelwertanalyse müssen die Daten balanciert sein.
Mittelwert
Formel
Der Durchschnitt der Beobachtungen für einen Faktor auf einer bestimmten Stufe. Minitab stellt den Mittelwert für jede Faktorstufe in der Grafik dar.
| Mittelwert von Faktor A auf der i-ten Stufe: |
 |
| Mittelwert von Faktor B auf der j-ten Stufe: |
 |
Notation
| Begriff | Beschreibung |
|---|---|
| yi. | Summe aller Beobachtungen auf der i-ten Stufe von Faktor A |
| y.j. | Summe aller Beobachtungen auf der j-ten Stufe von Faktor B |
| a | Anzahl der Stufen in A |
| b | Anzahl der Stufen in B |
| n | Anzahl der Fälle auf der i-ten Stufe von Faktor A und der j-ten Stufe von Faktor B |
Gesamtmittel (Mittellinie)
Formel
Der Durchschnitt aller Beobachtungen in der Stichprobe. Minitab verwendet das Gesamtmittel als Mittellinie in der Grafik der Haupteffekte.

Notation
| Begriff | Beschreibung |
|---|---|
| y... | Summe aller Beobachtungen in der Stichprobe |
| a | Anzahl der Stufen in A |
| b | Anzahl der Stufen in B |
| n | Anzahl der Fälle auf der i-ten Stufe von Faktor A und der j-ten Stufe von Faktor B |
Obere und untere Entscheidungsgrenze für Haupteffekte
Mit den Entscheidungsgrenzen wird angegeben, ob sich die Mittelwerte der Faktorstufen vom Gesamtmittel unterscheiden. Punkte, die jenseits der oberen Entscheidungsgrenze (OEG) oder der unteren Entscheidungsgrenze (UEG) liegen, unterscheiden sich statistisch vom Gesamtmittel.
Die Berechnung der oberen und der unteren Entscheidungsgrenze variiert entsprechend der Anzahl der Stufen des Faktors sowie der Anzahl der Beobachtungen auf jeder Stufe. Die nachfolgenden Formeln zeigen die obere und die untere Entscheidungsgrenze für Faktor A. Wenn Sie die Entscheidungsgrenzen für Faktor B berechnen möchten, ersetzen Sie die spezifischen Terme für Faktor A durch die entsprechenden Terme für Faktor B.
Zweistufiger Faktor
Die obere und die untere Entscheidungsgrenze für Faktor A werden wie folgt ausgedrückt:
- OEGA =
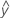 ...+ (0,5) * hα* Sqrt[(MSE) * (2 / n1)]
...+ (0,5) * hα* Sqrt[(MSE) * (2 / n1)] - UEGA =
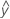 ...– (0,5) * hα* Sqrt[(MSE) * (2 / n1)]
...– (0,5) * hα* Sqrt[(MSE) * (2 / n1)]
Hierbei ist ha = Absolutwert (t(a / 2; abn – ab), MSE = mittleres Fehlerquadrat (aus einer ANOVA mit den Termen A, B und AB) und n1= Anzahl der Beobachtungen auf jeder Stufe des Faktors A.
Faktor mit mehr als zwei Stufen
- OEGA =
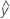 ...+ hα* Sqrt[MSE * (a – 1) / (a * n1)]
...+ hα* Sqrt[MSE * (a – 1) / (a * n1)] - UEGA =
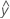 ...– hα* Sqrt[MSE * (a – 1) / (a * n1)]
...– hα* Sqrt[MSE * (a – 1) / (a * n1)]
Hierbei ist MSE = mittleres Fehlerquadrat (aus einer ANOVA mit den Termen A, B und AB), a = Anzahl der Faktorstufen in Faktor A und n1= Anzahl der Beobachtungen auf jeder Stufe des Faktors. Der kritische Wert hα hängt von Alpha, der Anzahl der dargestellten Mittelwerte und den Freiheitsgraden für den MSE ab. Die Werte von hα können Sie Tabelle B.1 in Anhang B in Nelson1 entnehmen.
Für Alpha-Werte außerhalb des Bereichs von 0,001 bis 0,1 werden die Entscheidungsgrenzen wie folgt ausgedrückt:
- OEGA =
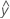 ...+ hα* Sqrt[MSE * (a – 1) / (a * n1)]
...+ hα* Sqrt[MSE * (a – 1) / (a * n1)] - UEGA =
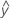 ...– hα* Sqrt[MSE * (a – 1) / (a * n1)]
...– hα* Sqrt[MSE * (a – 1) / (a * n1)]
Hierbei ist MSE = mittleres Fehlerquadrat (aus einer ANOVA mit den Termen A, B und AB), n1 = Anzahl der Beobachtungen auf jeder Stufe des Faktors und hα = Absolutwert (t(α2; df); wobei a2 = (1– (1– a )** (1 / a)) / 2 und df = nT – ab, wobei nT = Gesamtzahl der Beobachtungen in der Stichprobe.
- L. S. Nelson (1983). „Exact Critical Values for Use with the Analysis of Means“, Journal of Quality Technology, 15, S. 40-44.
Obere und untere Entscheidungsgrenze für Wechselwirkungseffekte
Die Entscheidungsgrenzen geben an, ob die Wechselwirkung signifikant ist. Punkte, die jenseits der oberen Entscheidungsgrenze (OEG) oder der unteren Entscheidungsgrenze (UEG) liegen, weisen darauf hin, dass die Wechselwirkung statistisch signifikant ist.
Nachfolgend sind die allgemeinen Formeln für die obere und die untere Entscheidungsgrenze für die Wechselwirkung zwischen den Faktoren A und B aufgeführt. Die Terme werden je nach Anzahl der Stufen und Beobachtungen in jedem Faktor unterschiedlich definiert.
- OEGAB = hα* Sqrt[MSE * (q / (a * b * n)]
- UEGAB = –hα* Sqrt[MSE * (q / (a * b * n)]
Hierbei sind ha = Absolutwert (t(α2, dfe)), a = Anzahl der Stufen in Faktor A, b = Anzahl der Stufen in Faktor B, n = Anzahl der Beobachtungen für jede Wechselwirkung zwischen Faktoren, q = Freiheitsgrade für Wechselwirkungseffekte, (a – 1)(b – 1) und dfe = Freiheitsgrade für Fehler, abn – ab.
Faktoren A und B weisen zwei Stufen auf
- α2 = a / 2
Faktor A weist zwei Stufen und Faktor B mehr als zwei Stufen auf
- α2 = (1 – (1 – a )** (1 / b)) / 2
wobei a = Anzahl der Stufen in Faktor A und b = Anzahl der Stufen in Faktor B.
Faktor A weist mehr als zwei Stufen und Faktor B zwei Stufen auf
- α2 = (1 – (1 – a )** (1 / a)) / 2
wobei a = Anzahl der Stufen in Faktor A und b = Anzahl der Stufen in Faktor B.
Faktoren A und B weisen mehr als zwei Stufen auf
- α2 = (1 – (1 – a )** (1 / a * b)) / 2
wobei a = Anzahl der Stufen in Faktor A und b = Anzahl der Stufen in Faktor B.
