In diesem Thema
Methode
Die Mittelwertanalyse ist ein Verfahren, mit dem ermittelt wird, ob sich die Mittelwerte einzelner Faktorstufen vom Gesamtmittel (dem Mittelwert aller Beobachtungen in einem Faktor) unterscheiden. Im Folgenden sind die Schritte aufgeführt, mit denen Minitab ANOM-Ergebnisse für ein einfaches Modell berechnet:
- Der Mittelwert bei jeder Faktorstufe wird berechnet: y̅i. (i = 1, …, r).
- Das Gesamtmittel aller Beobachtungen y... wird berechnet.
- sp, ein Schätzwert der Standardabweichung einer Beobachtung, wird berechnet.
- Der Wert hα wird ermittelt; dieser Wert entspricht dem für den Test gewählten Signifikanzniveau, und er wird für die obere und untere Entscheidungsgrenze verwendet.
- Die obere und die untere Entscheidungsgrenze (OEG und UEG) werden berechnet.
- Die Mittelwerte der einzelnen Faktorstufen mit der oberen und der unteren Referenzlinie sowie die Mittellinie beim Gesamtmittel werden grafisch dargestellt.
Mittelwert
Formel
Der Durchschnitt der Beobachtungen auf den einzelnen Faktorstufen. Minitab stellt den Mittelwert für jede Faktorstufe in der Grafik dar.
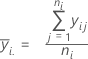
Notation
| Begriff | Beschreibung |
|---|---|
| ni | Anzahl der Beobachtungen auf Faktorstufe i |
| yij | Wert der j-ten Beobachtung auf der i-ten Faktorstufe |
Gesamtmittel (Mittellinie)
Formel
Hierbei handelt es sich um den Durchschnitt aller Beobachtungen für alle Faktorstufen. Minitab verwendet das Gesamtmittel als Mittellinie in der Grafik.
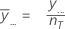
Notation
| Begriff | Beschreibung |
|---|---|
| y... | Summe aller Beobachtungen in der Stichprobe |
| nT | Gesamtzahl der Beobachtungen |
Standardabweichung (StdAbw)
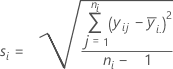
Notation
| Begriff | Beschreibung |
|---|---|
| yij | Beobachtungen auf der i-ten Faktorstufe |
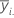 | Mittelwert der Beobachtungen auf der i-ten Faktorstufe |
| ni | Anzahl der Beobachtungen auf der i-ten Faktorstufe |
Zusammengefasste Standardabweichung
Hierbei handelt es sich um einen Schätzwert der Streuung für alle Faktorstufen. Die zusammengefasste Standardabweichung wird verwendet, um die Entscheidungsgrenzen zu berechnen.
Formel
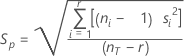
Notation
| Begriff | Beschreibung |
|---|---|
| r | Anzahl der Stufen |
| nT | Gesamtzahl der Beobachtungen |
Obere und untere Entscheidungsgrenze
Mit den Entscheidungsgrenzen wird angegeben, ob sich die Mittelwerte der Faktorstufen vom Gesamtmittel unterscheiden. Punkte, die jenseits der oberen Entscheidungsgrenze (OEG) oder der unteren Entscheidungsgrenze (UEG) liegen, unterscheiden sich statistisch vom Gesamtmittel.
Die Berechnung der oberen und der unteren Entscheidungsgrenze variiert entsprechend der Anzahl der Stufen des Faktors sowie der Anzahl der Beobachtungen auf jeder Stufe.
Zwei-Stufen-Faktor mit gleicher Anzahl von Beobachtungen auf jeder Stufe
- OEG = y.. + hα sp* Sqrt(1/ nT)
- UEG = y.. – hα sp* Sqrt(1/ nT)
Hierbei sind hα = Absolutwert (t(a / 2, nT – 2)), sp = zusammengefasste Standardabweichung und nT = Gesamtzahl der Beobachtungen.
Faktor mit mehr als zwei Stufen und einer gleichen Anzahl von Beobachtungen auf jeder Stufe
- OEG = y.. + hα sp* Sqrt[(r–1) / (rn1)]
- UEG = y.. – hα sp* Sqrt[(r–1) / (rn1)]
Hierbei sind r = Anzahl der Stufen im Faktor und n1 = Anzahl der Beobachtungen auf jeder Stufe.
Die Freiheitsgrade sind (n1– 1) * r.
Für Alpha-Werte außerhalb des Bereichs von 0,001 bis 0,1 werden die Entscheidungsgrenzen wie folgt ausgedrückt:
- OEG = y.. + hα sp* Sqrt[(nT – n1) / (nT* n1)]
- UEG = y.. – hα sp* Sqrt[(nT – n1) / (nT* n1)]
Hierbei sind hα = Absolutwert (t(α2, df) und α2 = (1– (1– a )** (1 / r)) / 2 und df = nT – r.
Informationen zum Berechnen von hα für α-Werte zwischen 0,001 und 0,1 finden Sie in Nelson1.
Faktor mit mindestens zwei Stufen und einer ungleichen Anzahl von Beobachtungen auf jeder Stufe
- OEGi = y.. + hα sp* Sqrt[(nT – ni) / (nT* ni)]
- UEGi = y.. – hα sp* Sqrt[(nT – ni) / (nT* ni)]
- L. S. Nelson (1983). „Exact Critical Values for Use with the Analysis of Means“, Journal of Quality Technology, 15, 40–44.
