Alle Produktleistungsberichte für Produktbericht

In diesem Thema

Bericht 7: Produktleistung
Bericht 8A: Produkt-Benchmarks (Vergleich von DPMO und Z.Bench)
Bericht 8B: Produkt-Benchmarks (Vergleich von Z.Shift und Z.Bench)
Bericht 8C: Produkt-Benchmarks (Prozessfähigkeit, Komplexität, Beherrschung)

Bericht 7: Produktleistung

Im Bericht „Produktleistung“ werden die gesamten Leistungsmesswerte berechnet, die beim Zusammenfassen von Teilen der unteren Ebene in einer Einheit der oberen Ebene entstehen.

Six Sigma-Produktbericht

Zusammenfassende Statistiken Beob Beob Fehlermögl. Kor Kor Komponente Fehler Einh pro Einheit Kmplx Kor Fehl Einh Gsmt.-Fehlermögl. 1 77 184 56 1 32,641 78 4368 2 3 907 95 6 1,548 468 44460 3 59 750 59 5 30,680 390 23010 4 28 567 79 4 15,407 312 24648 5 73 829 64 5 34,343 390 24960 6 28 132 30 1 16,545 78 2340 7 1 547 76 3 0,428 234 17784 8 5 726 30 5 2,686 390 11700 9 2 78 28 1 2,000 78 2184 10 89 655 55 4 42,394 312 17160 11 74 715 98 5 40,364 390 38220 12 3 453 36 3 1,550 234 8424 13 99 233 10 1 33,142 78 780 14 49 726 80 5 26,322 390 31200 15 78 832 81 5 36,563 390 31590 16 50 783 1 5 24,904 390 390 17 88 807 10 5 42,528 390 3900 18 61 123 40 1 38,683 78 3120 19 4 906 57 6 2,066 468 26676 20 21 696 48 5 11,767 390 18720 Gesamt 436,561 78 335634

Komponente DPU DPMO Z.Shift Z.ST YTP RTY 1 0,418478 7472,8 1,500 3,934 0,657014 0,657014 2 0,003308 34,8 1,500 5,478 0,996698 0,980350 3 0,078667 1333,3 1,500 4,504 0,924299 0,674627 4 0,049383 625,1 1,500 4,727 0,951802 0,820704 5 0,088058 1375,9 1,500 4,494 0,915652 0,643655 6 0,212121 7070,7 1,500 3,954 0,808257 0,808257 7 0,001828 24,1 1,500 5,565 0,998173 0,994530 8 0,006887 229,6 1,500 5,004 0,993136 0,966147 9 0,025641 915,8 1,500 4,616 0,974673 0,974673 10 0,135878 2470,5 1,500 4,311 0,872802 0,580315 11 0,103497 1056,1 1,500 4,574 0,901630 0,595856 12 0,006623 184,0 1,500 5,062 0,993399 0,980327 13 0,424893 42489,3 1,500 3,223 0,647793 0,647793 14 0,067493 843,7 1,500 4,640 0,934708 0,713475 15 0,093750 1157,4 1,500 4,547 0,910461 0,625614 16 0,063857 63857,0 1,500 3,023 0,936143 0,718970 17 0,109046 10904,6 1,500 3,794 0,896152 0,577976 18 0,495935 12398,4 1,500 3,745 0,607116 0,607116 19 0,004415 77,5 1,500 5,283 0,995595 0,973857 20 0,030172 628,6 1,500 4,726 0,970269 0,859926 Gesamt 1300,7 1,500 4,511 0,003598

Komponente

Optionale Spalte für Komponentennamen. Wenn Sie keine Namen angeben, weist Minitab Zahlen als ID-Nummern zu.

Beob Fehler

Anzahl der beobachteten Fehler.

Beob Einh

Anzahl der Einheiten der einzelnen beobachteten Komponenten.

Fehlermögl. pro Einheit

Anzahl der Möglichkeiten (von Fehlern) pro Einheit.

Weitere Informationen finden Sie unter Was sind Möglichkeiten pro Einheit?.

Kmplx

Anzahl der Komplexität für die einzelnen Komponenten. Sie können die beobachteten Einheiten und Fehler korrigieren, indem Sie Anteile für die einzelnen Komponenten festlegen. Beispiel: Zum Herstellen einer größeren Baugruppe werden 1 Einheit der Komponente 1, 6 Einheiten der Komponente 2, 5 Einheiten der Komponente 3 usw.

Die Komplexitätsspalte ist nicht erforderlich, wenn jedoch Komplexitätswerte verwendet werden, mindert dies die Auswirkungen einer disproportionalen Stichprobe. Wenn keine Anteile vorliegen, geben Sie in der gesamten Spalte in allen Zeilen den Wert 1 ein.

Weitere Informationen finden Sie unter Was ist Komplexität?.

Kor Fehl

Beobachtete Fehler werden anhand der Komplexitätsinformationen korrigiert (oder gewichtet). Wenn keine Komplexitätseinheiten angegeben sind, sind die korrigierten Fehler mit den beobachteten Fehlern identisch.

Kor Einh

Beobachtete Einheiten werden anhand der Komplexitätsinformationen korrigiert (oder gewichtet). Wenn keine Komplexitätseinheiten angegeben sind, sind die korrigierten Einheiten mit den beobachteten Einheiten identisch. Alle Komponenten mit gleicher Komplexität weisen die gleichen korrigierten Einheiten auf. Im Beispiel weisen die beiden Komponenten 7 und 12 die Komplexität 3 und 234 korrigierte Einheiten auf.

Kor Gsmt.-Fehlermögl.

Diese Spalte wird durch Multiplikation von „Kor Einh“ und „Fehlermögl. pro Einheit“ berechnet. Wenn die Anzahl der Einheiten nicht korrigiert wird, sind die Gesamtmöglichkeiten zugunsten größerer Anzahlen beobachteter Einheiten schief, was sich auf die Berechnungen der Leistungsstatistik auswirken würde. Das Verwenden von Komplexitätswerten verringert die Auswirkungen einer disproportionalen Stichprobe.

DPU

Die Fehler pro Einheit werden durch Division der Anzahl der Fehler durch die Anzahl der Einheiten berechnet.

DPMO

Die Fehler pro Million Möglichkeiten werden durch Division von „Kor Einh“ durch „Kor Gsmt.-Fehlermögl.“ und anschließender Multiplikation mit 1 Million berechnet.

Wenn die Anzahl der Einheiten nicht korrigiert wird, sind die Gesamtmöglichkeiten zugunsten von Komponenten mit größeren Anzahlen der beobachteten Einheiten schief.

Z.Shift

Werte zum Darstellen des angenommenen Sigma-Shifts (Long-Term). Wenn kein Wert angegeben wird, verwendet Minitab 1,5 als Standardwert.

Weitere Informationen finden Sie unter Z.Bench als Schätzwert der Sigma-Prozessfähigkeit.

Z.ST

Z-Werte werden aus DPMO und Z.Shift berechnet.

YTP

Komponentenausbeute für die einzelnen Komponenten. Es handelt sich um die Wahrscheinlichkeit, dass keine der Möglichkeiten in der Komponente zu einem Fehler führt.

Weitere Informationen finden Sie unter Was sind Komponentenausbeute (YTP) und Gesamtkomponentenausbeute (RTY)?.

RTY

Gesamtkomponentenausbeute für die einzelnen Komponenten. Die Wahrscheinlichkeit, dass eine fehlerfreie Einheit der Komponente 2 vorliegt, entspricht der YTP bzw. Gesamtkomponentenausbeute 0,996698. Für eine größere Baugruppe benötigen Sie 6 Einheiten der Komponente 2. Die Wahrscheinlichkeit, dass 6 fehlerfreie Einheiten der Komponente 2 vorliegen, entspricht der RTY bzw. Gesamtkomponentenausbeute (0,996698)⁶ = 0,980350.

Weitere Informationen finden Sie unter Was sind Komponentenausbeute (YTP) und Gesamtkomponentenausbeute (RTY)?.

Bericht 8A: Produkt-Benchmarks (Vergleich von DPMO und Z.Bench)

Der Bericht „Produkt-Benchmarks“ (Vergleich von DPMO und Z.Bench) enthält eine grafische Ansicht der Benchmark-Statistiken für die Gruppe von Komponenten, die im Produktbericht aufgeführt werden.

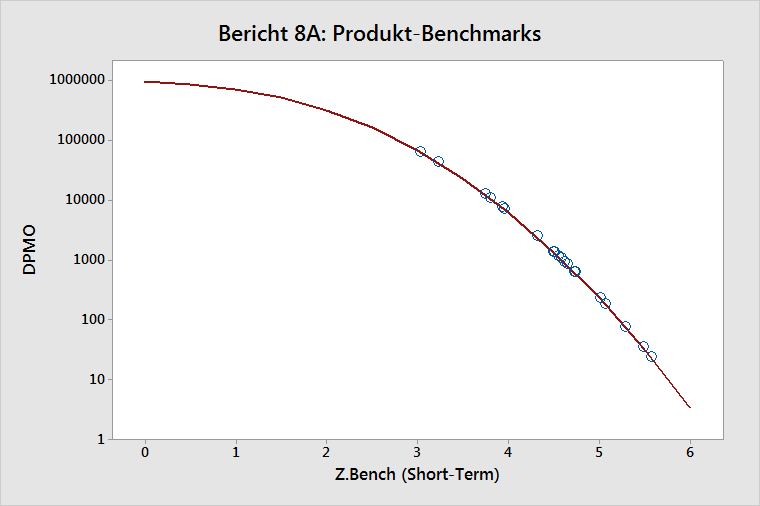
DPMO ist ein Maß für die Langzeitleistung. Z.Bench ST ist ein Maß für die Kurzzeitleistung.

Die Positionen der Punktcluster veranschaulichen, an welchen Stellen sich die Prozessfähigkeit tendenziell konzentriert. Im obigen Beispiel befindet sich ein Cluster knapp unterhalb von 4 auf der Z.ST-Skala und weitere Cluster nahe dem Wert von 4,5. Daher bewegen sich viele der hier verwendeten Prozesse von knapp unterhalb 4 bis knapp oberhalb von 4 Sigma. Diese Beobachtung ist relativ typisch.

Bericht 8B: Produkt-Benchmarks (Vergleich von Z.Shift und Z.Bench)

Der Bericht „Produkt-Benchmarks“ (Vergleich von Z.Shift und Z.Bench) bietet eine weitere Ansicht der Benchmark-Statistiken für die Gruppe von Komponenten, die im Produktbericht aufgeführt werden.

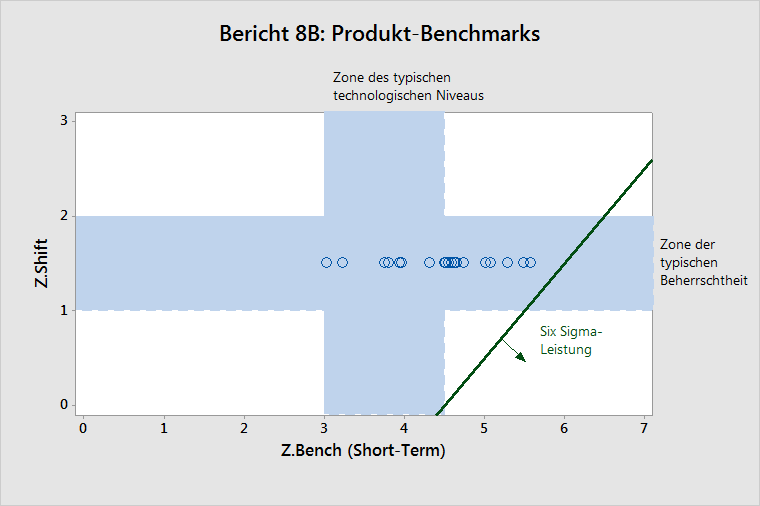
In dieser Grafik werden die Beherrschbarkeit der einzelnen Komponenten (Z.Shift) und die Prozessfähigkeit der einzelnen Komponenten (Z.ST) verglichen. Die Z.Shift-Werte liegen in der Regel auf dem horizontalen Band (Zone der typischen Beherrschtheit) und die Z.ST-Werte auf dem vertikalen Band (Zone der typischen technologischen Niveaus).

Die Six Sigma-Leistungsfähigkeit wird bei hohen Z.Bench-Niveaus und niedrigen Z.Shift-Niveaus erreicht.

Z.Shift

Kleine Z.Shift-Werte entsprechen Merkmalen, die sehr gut unter Kontrolle sind.
Große Z.Shift-Werte entsprechen Merkmalen, die sehr schlecht unter Kontrolle sind.

Z.Bench ST

Große Z.Bench-Werte entsprechen Merkmalen, die eine technologische Überlegenheit darstellen.
Kleine Z.Bench-Werte entsprechen Merkmalen, die eine technologische Unterlegenheit darstellen.

Im obigen Beispiel weisen alle Komponenten einen Z.Shift von 1,5 Sigma auf. Dies entspricht der Standardeinstellung, wenn die tatsächlichen Z.Shift-Werte unbekannt sind. Etwa die Hälfte der Komponenten weist Z.Bench-Werte in der Zone der typischen technologischen Niveaus auf. Die Werte der anderen Hälfte der Komponenten liegen im rechten Bereich; dies deutet auf eine überdurchschnittliche Prozessfähigkeit hin.

Bericht 8C: Produkt-Benchmarks (Prozessfähigkeit, Komplexität, Beherrschung)

Ohne Komplexitätsinformationen

Wenn Sie keine Komplexitätsinformationen einbinden, enthält der Bericht „Produkt-Benchmarks“ die folgenden Grafiken:

YTP: Ein umgekehrtes Pareto-Diagramm der Komponentenausbeuten (YTP)
Fehlermögl. pro Einheit: Fehlermöglichkeiten pro Einheit für die Komponenten, angeordnet nach YTP-Werten
Z.ST: Z.ST-Werte für die Komponenten, angeordnet nach YTP-Werten
Z.Shift: Z.Shift-Werte für die Komponenten, angeordnet nach YTP-Werten

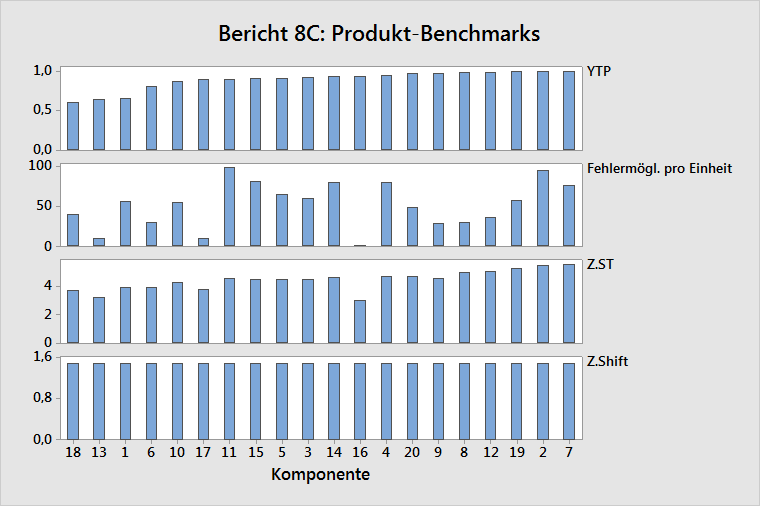
Ermitteln Sie in der YTP-Grafik die Komponenten mit der schlechtesten Qualität, und untersuchen Sie anschließend die unteren Diagramme, um zu ermitteln, ob das Problem auf eine hohe Komplexität (Anzahl der Fehlermöglichkeiten), eine geringe Prozessfähigkeit (Z.ST) oder eine mangelhafte Beherrschung (Z.Shift) zurückzuführen ist.

Im obigen Beispiel weist die Komponente 18 die schlechteste Qualität, eine moderate Anzahl von Fehlermöglichkeiten und eine unterdurchschnittliche Prozessfähigkeit auf. Die Verbesserung der Prozessfähigkeit wirkt sich am stärksten auf die Verbesserung der Qualität aus.

Mit Komplexitätsinformationen

Wenn Sie Komplexitätsinformationen einbinden, enthält der Bericht „Produkt-Benchmarks“ die folgenden Grafiken:

RTY: Ein umgekehrtes Pareto-Diagramm der Gesamtkomponentenausbeuten (RTY)
Gesamt Fehlermögl. pro Einheit: Fehlermöglichkeiten pro Einheit für die Komponenten, angeordnet nach RTY-Werten
Z.ST: Z.ST-Werte für die Komponenten, angeordnet nach RTY-Werten
Z.Shift: Z.Shift-Werte für die Komponenten, angeordnet nach RTY-Werten

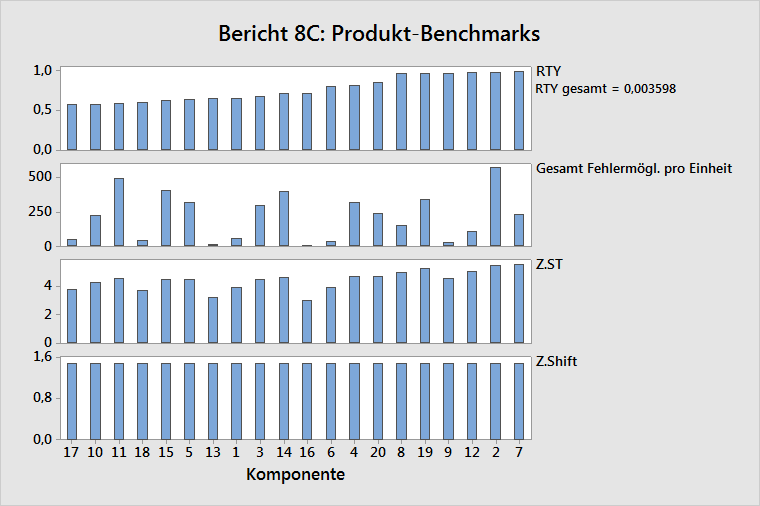
Die Gesamtkomponentenausbeute (RTY) stellt die Wahrscheinlichkeit dar, dass eine einzelne Einheit der gesamten Gruppe von Komponenten ohne Fehler hergestellt werden kann. Die Komponenten mit den kleinsten RTY-Werten auf dem Komponentenniveau tragen am meisten zur Gesamt-RTY bei. Daher ist die Verbesserung dieser Komponenten für die Verbesserung von RTY entscheidend.

Im obigen Beispiel weist Komponente 17 die kleinste RTY, eine kleine Anzahl von Fehlermöglichkeiten und eine geringe Prozessfähigkeit auf. Das Anheben der durchschnittlichen Z.ST für Komponente 17 wirkt sich am stärksten auf die Verbesserung der Qualität aus und verbessert damit die Gesamtproduktqualität.

Komponente 11 als drittschlechteste Komponente weist eine hohe Anzahl von Fehlermöglichkeiten und eine gute Prozessfähigkeit auf. Das Verringern der Anzahl von Fehlermöglichkeiten wirkt sich am stärksten auf die Qualitätsverbesserung der Komponente 11 aus, da die Prozessfähigkeit bereits recht gut ist.