In diesem Thema
- Konstanten für erwartungstreue Schätzung zum Schätzen der Langzeit- und Kurzzeitstandardabweichung
- Kurzzeitstandardabweichungen
- Langzeitstandardabweichungen
- Langzeitprozessmittelwert
- Langzeitprozessstandardabweichung
- Kurzzeitprozessmittelwert
- Kurzzeitprozessstandardabweichung
- Prozessfähigkeitsstatistiken
- Freiheitsgrade
- Wahrscheinlichkeiten
- Z.Bench-Statistiken
Konstanten für erwartungstreue Schätzung zum Schätzen der Langzeit- und Kurzzeitstandardabweichung
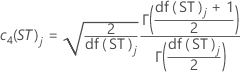
- Konstante für erwartungstreue Schätzung zum Schätzen der Langzeitstandardabweichung
-
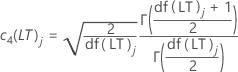
- Konstante für erwartungstreue Schätzung zum Schätzen der Kurzzeitstandardabweichung
-
Dabei gilt Folgendes:
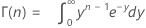
Notation
| Begriff | Beschreibung |
|---|---|
| c4(LT)j | Konstante für erwartungstreue Schätzung für Langzeitberechnungen für kumulierte j-te Teilgruppe |
| c4(ST)j | Konstante für erwartungstreue Schätzung für Kurzzeitberechnungen für kumulierte j-te Teilgruppe |
| df(LT)j | Langzeitfreiheitsgrade bei j-ter Teilgruppe |
| df(ST)j | Kurzzeitfreiheitsgrade bei j-ter Teilgruppe |
Kurzzeitstandardabweichungen
- Kurzzeitstandardabweichung mit Konstante für erwartungstreue Schätzung (Standardeinstellung)
-
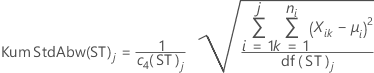
- Kurzzeitstandardabweichung ohne Konstante für erwartungstreue Schätzung
-
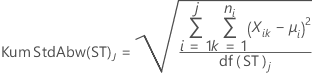
Dabei gilt Folgendes:
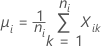
Notation
| Begriff | Beschreibung |
|---|---|
| Kum StdAbw(ST)j | Kumulierte Kurzzeitstandardabweichung bis zur j-ten Teilgruppe |
| c4(ST)j | Konstante für erwartungstreue Schätzung für Kurzzeitberechnungen für kumulierte j-te Teilgruppe |
| df(ST)j | Kurzzeitfreiheitsgrade bei j-ter Teilgruppe |
Langzeitstandardabweichungen
- Langzeitstandardabweichung ohne Konstante für erwartungstreue Schätzung (Standardeinstellung)
-
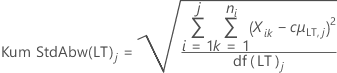
- Langzeitstandardabweichung mit Konstante für erwartungstreue Schätzung
-
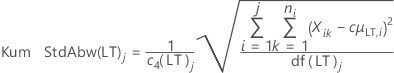
Dabei gilt Folgendes:
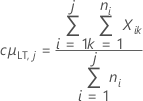
Notation
| Begriff | Beschreibung |
|---|---|
| Kum StdAbw(LT)j | Kumulierte Langzeitstandardabweichung bis zur j-ten Teilgruppe |
| c4(LT)j | Konstante für erwartungstreue Schätzung für Langzeitberechnungen für kumulierte j-te Teilgruppe |
| df(LT)j | Langzeitfreiheitsgrade bei j-ter Teilgruppe |
Langzeitprozessmittelwert
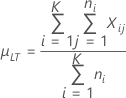
Notation
| Begriff | Beschreibung |
|---|---|
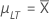
| µLT |
Langzeitmittelwert oder Prozessmittelwert μLT = cμLT,K Hinweis
|
Langzeitprozessstandardabweichung
σLT = Kum StdAbw(LT)K
Kurzzeitprozessmittelwert
- Wenn der Sollwert angegeben ist
- μST = T
- Wenn beide Spezifikationsgrenzen angegeben sind (kein Sollwert)

- Wenn eine Spezifikationsgrenze angegeben ist (kein Sollwert)
- μST = μLT
Notation
| Begriff | Beschreibung |
|---|---|
| µST | Kurzzeitmittelwert |
| T | Soll |
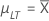
| µLT |
Langzeitmittelwert oder Prozessmittelwert Hinweis
|
Kurzzeitprozessstandardabweichung
σST = Kum StdAbw(ST)K
Weitere Informationen finden Sie unter Auswahl der Zentralwerte für Kurzzeitstatistiken durch Minitab für Prozessbericht.
Prozessfähigkeitsstatistiken
- CCpk
-
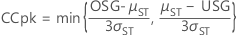
- Cp
-
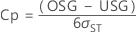
- Cpk
-
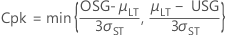
- CPL
-

- CPU
-
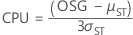
Hinweis
Cp, Cpk und CCpk stellen die potenzielle Prozessfähigkeit dar. Deswegen wird bei diesen Formeln die Kurzzeitstreuung verwendet.
- Pp
-
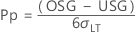
- Ppk
-
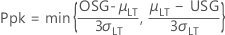
- PPL
-
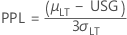
- PPU
-
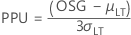
Hinweis
Pp und Ppk stellen die tatsächliche Prozessleistung dar. Deswegen wird bei diesen Formeln die Langzeitstreuung verwendet.
Freiheitsgrade
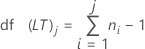
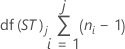
Notation
| Begriff | Beschreibung |
|---|---|
| df(LT)j | Langzeitfreiheitsgrade bei j-ter Teilgruppe |
| df(ST)j | Kurzzeitfreiheitsgrade bei j-ter Teilgruppe |
Wahrscheinlichkeiten
- P.USG(LT)j
-
Langzeitwahrscheinlichkeit für Wert kleiner oder gleich der unteren Spezifikationsgrenze bei j-ter Teilgruppe
P.USG(LT) j = 1 – Φ(Z.USG(LT)j)
- P.USG(ST) j
-
Kurzzeitwahrscheinlichkeit für Wert kleiner oder gleich der unteren Spezifikationsgrenze bei j-ter Teilgruppe
P.USG(ST) j = 1 – Φ(Z.USG(ST)j)
- P.OSG(LT) j
-
Langzeitwahrscheinlichkeit für Wert größer oder gleich der oberen Spezifikationsgrenze bei j-ter Teilgruppe
P.OSG(LT) j = 1 – Φ(Z.OSG(LT)j)
- P.OSG(ST) j
-
Kurzzeitwahrscheinlichkeit für Wert größer oder gleich der oberen Spezifikationsgrenze bei j-ter Teilgruppe
P.OSG(ST) j = 1 – Φ(Z.USG(ST)j)
- P.Gesamt(LT) j
-
Gesamte Langzeitwahrscheinlichkeit für Wert außerhalb der Spezifikationsgrenzen bei j-ter Teilgruppe
P.Gesamt(LT) j = P.OSG(LT)j + P.USG(LT)j
- P.Gesamt(ST)j
-
Gesamte Kurzzeitwahrscheinlichkeit für Wert außerhalb der Spezifikationsgrenzen bei j-ter Teilgruppe
P.Gesamt(ST)j = P.OSG(ST)j + P.USG(ST)j
Z.Bench-Statistiken
- Z.Bench(LT)j
-
Benchmark-Z (Long-Term) bei j-ter Teilgruppe
Z.Bench(LT)j = Φ–1(P.Gesamt(LT)j)
- Z.Bench(ST)j
-
Benchmark-Z (Short-Term) bei j-ter Teilgruppe
Z.Bench(ST)j = Φ–1(P.Gesamt(ST)j)
- Z.USG(LT)j
-
Z-Wert (Long-Term) für untere Spezifikationsgrenze bei j-ter Teilgruppe
Z.USG(LT)j = (μLT – USG) / Kum StdAbw(LT)j
- Z.USG(ST)j
-
Z-Wert (Short-Term) für untere Spezifikationsgrenze bei j-ter Teilgruppe
Z.USG(ST)j = (μST – USG) / Kum StdAbw(ST)j
- Z.OSG(LT)j
-
Z-Wert (Long-Term) für obere Spezifikationsgrenze bei j-ter Teilgruppe
Z.OSG(LT)j = (OSG – μLT) / Kum StdAbw(LT)j
- Z.OSG(ST)j
-
Z-Wert (Short-Term) für obere Spezifikationsgrenze bei j-ter Teilgruppe
Z.OSG(ST)j = (OSG – μST) / Kum StdAbw(ST)j
- Z.Shiftj
-
Shift-Faktor bei j-ter Teilgruppe
Z.Shiftj = Z.Bench(ST)j – Z.Bench(LT)j