In diesem Thema
Schritt 1: Vorliegen einer Normalverteilung in den Daten prüfen
Minitab stellt Toleranzintervalle für die Normalverteilungsmethode und für die verteilungsfreie Methode bereit. Wenn Sie mit Sicherheit annehmen können, dass die Daten einer Normalverteilung folgen, können Sie das Toleranzintervall gemäß der Normalverteilungsmethode verwenden. Wenn Sie nicht mit Sicherheit annehmen können, dass die Daten einer Normalverteilung folgen, müssen Sie das Toleranzintervall gemäß der verteilungsfreien Methode verwenden.
Um zu ermitteln, ob Sie annehmen können, dass die Daten einer Normalverteilung folgen, vergleichen Sie den p-Wert aus dem Test auf Normalverteilung mit dem Signifikanzniveau (α). Ein Signifikanzniveau von 0,05 bedeutet ein Risiko der Schlussfolgerung, dass die Daten keiner Normalverteilung folgen, wenn sie tatsächlich einer Normalverteilung folgen, von 5%.
- p-Wert ≤ α: Die Daten folgen keiner Normalverteilung (H0 verwerfen)
- Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, können Sie schlussfolgern, dass die Daten keiner Normalverteilung folgen. In diesem Fall müssen Sie das Toleranzintervall gemäß der verteilungsfreien Methode verwenden.
- p-Wert > α: Es liegen nicht genügend Anzeichen vor, um zu folgern, dass die Daten keiner Normalverteilung folgen (H0 nicht zurückweisen)
- Wenn der p-Wert größer als das Signifikanzniveau ist, liegen nicht genügend Anzeichen vor, um zu schlussfolgern, dass die Daten keiner Normalverteilung folgen. In diesem Fall können Sie das Toleranzintervall gemäß der Normalverteilungsmethode verwenden.
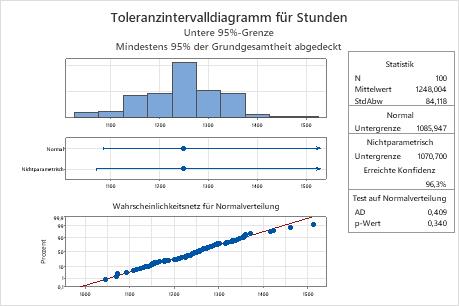
Wichtigste Ergebnisse: p-Wert
In diesen Ergebnissen ist der p-Wert 0,340 und somit größer als das Signifikanzniveau von 0,05. Da Sie annehmen können, dass die Daten einer Normalverteilung folgen, können Sie das Toleranzintervall gemäß der Normalverteilungsmethode verwenden.
Schritt 2: Gemäß der passenden Methode berechnetes Toleranzintervall untersuchen
- Beidseitig
- Verwenden Sie ein beidseitiges Intervall, um das Intervall zu bestimmen, das einen bestimmten Prozentsatz der Messwerte der Grundgesamtheit enthält.
- Obergrenze
- Verwenden Sie eine Obergrenze, um das Intervall zu bestimmen, das angibt, dass ein bestimmter Prozentsatz der Messwerte der Grundgesamtheit nicht größer als eine Obergrenze sein wird.
- Untergrenze
- Verwenden Sie eine Untergrenze, um das Intervall zu bestimmen, das angibt, dass ein bestimmter Prozentsatz der Messwerte der Grundgesamtheit nicht kleiner als eine Untergrenze sein wird.
