In diesem Thema
Konfidenzniveau
Da Stichproben von Daten zufällig sind, ist es unwahrscheinlich, dass zwei Stichproben aus derselben Grundgesamtheit zu identischen Toleranzintervallen führen. Wenn Sie jedoch viele Stichproben erfassen, enthält ein gewisser Prozentsatz der resultierenden Toleranzintervalle den Mindestanteil der Grundgesamtheit, den Sie angeben.
Das Konfidenzniveau gibt die Wahrscheinlichkeit an, dass das Toleranzintervall tatsächlich den Mindestprozentsatz umfasst. Ein Techniker möchte beispielsweise mit einer Konfidenz von 98 % den Bereich ermitteln, in den 99% des künftigen Produkts fallen. Das Konfidenzniveau für das Toleranzintervall beträgt 98%.
Methode
| Konfidenzniveau | 98% |
|---|---|
| Prozent der Grundgesamtheit in Intervall | 99% |
Hinweis
Sie können das Konfidenzniveau für die Analyse im Dialogfeld „Optionen“ angeben. Minitab zeigt das Ziel-Konfidenzniveau in der Methodentabelle an. In der Standardeinstellung beträgt das Konfidenzniveau 95%. Bei der verteilungsfreien Methode berechnet Minitab das erreichte Konfidenzniveau. Das erreichte Konfidenzniveau ist das exakte Konfidenzniveau, das von Minitab berechnet wird. In der Regel ist das erreichte Konfidenzniveau größer oder gleich dem Ziel-Konfidenzniveau, sofern der Stichprobenumfang nicht zu klein ist.
Prozent der Grundgesamtheit in Intervall
Der Prozentsatz der Grundgesamtheit im Intervall gibt den Mindestprozentsatz der Grundgesamtheit an, den das Toleranzintervall umfassen soll. Ein Techniker möchte beispielsweise mit einer Konfidenz von 98% den Bereich ermitteln, in den 99% des künftigen Produkts fallen. Der Prozentsatz der Grundgesamtheit im Toleranzintervall beträgt 99%.
Methode
| Konfidenzniveau | 98% |
|---|---|
| Prozent der Grundgesamtheit in Intervall | 99% |
N
Der Stichprobenumfang (N) gibt die Gesamtzahl der Beobachtungen in der Stichprobe an. In diesen Daten beträgt der Stichprobenumfang 400.
Statistik
| Variable | N | Mittelwert | StdAbw |
|---|---|---|---|
| C1 | 400 | 0,604 | 3,671 |
Mittelwert
Der Mittelwert fasst die Stichprobenwerte in einem einzigen Wert zusammen, der das Zentrum der Daten darstellt. Der Mittelwert ist der Durchschnitt der Daten; hierbei handelt es sich um die Summe aller Beobachtungen dividiert durch die Anzahl der Beobachtungen.
In diesen Daten ist der Mittelwert 0,604.
Statistik
| Variable | N | Mittelwert | StdAbw |
|---|---|---|---|
| C1 | 400 | 0,604 | 3,671 |
StdAbw
Die Standardabweichung ist das am häufigsten verwendete Maß für die Streuung bzw. die Streubreite der Daten um den Mittelwert.
Eine größere Standardabweichung verweist darauf, dass die Daten breiter um den Mittelwert gestreut sind, und führt zu einem breiteren Toleranzintervall. Eine kleinere Standardabweichung verweist darauf, dass die Daten enger um den Mittelwert gestreut sind, und führt zu einem engeren Toleranzintervall.
In diesen Daten beträgt die Standardabweichung 3,671.
Statistik
| Variable | N | Mittelwert | StdAbw |
|---|---|---|---|
| C1 | 400 | 0,604 | 3,671 |
Normalverteilungsmethode
Ein Toleranzintervall ist ein Wertebereich für ein bestimmtes Qualitätsmerkmal eines Produkts, der wahrscheinlich einen angegebenen Prozentsatz der künftig produzierten Produkte abdeckt. Verwenden Sie das Toleranzintervall gemäß der Normalverteilungsmethode, wenn Sie mit Sicherheit annehmen können, dass die Stichprobe aus einer normalverteilten Grundgesamtheit stammt.
Wenn die Daten einer Normalverteilung folgen, ist die Normalverteilungsmethode präziser und effizienter als die verteilungsfreie Methode. Mit der Normalverteilungsmethode erzielen Sie kleinere Fehlerspannen bei einer geringeren Zahl von Beobachtungen.
Die Normalverteilungsmethode ist gegenüber großen Abweichungen von der Normalverteilung nicht robust. Wenn Sie sich nicht sicher sind, welche Verteilung die Grundgesamtheit aufweist, oder Ihnen bekannt ist, dass es sich dabei um eine Nicht-Normalverteilung handelt, verwenden Sie die verteilungsfreie Methode.
Interpretation
- Beidseitig
- Verwenden Sie ein beidseitiges Intervall, um das Intervall zu bestimmen, das einen bestimmten Prozentsatz der Messwerte der Grundgesamtheit enthält.
- Obergrenze
- Verwenden Sie eine Obergrenze, um das Intervall zu bestimmen, das angibt, dass ein bestimmter Prozentsatz der Messwerte der Grundgesamtheit nicht größer als eine Obergrenze sein wird.
- Untergrenze
- Verwenden Sie eine Untergrenze, um das Intervall zu bestimmen, das angibt, dass ein bestimmter Prozentsatz der Messwerte der Grundgesamtheit nicht kleiner als eine Untergrenze sein wird.
Verteilungsfreie Methode
Ein Toleranzintervall ist ein Wertebereich für ein bestimmtes Qualitätsmerkmal eines Produkts, der wahrscheinlich einen angegebenen Anteil der künftig produzierten Produkte abdeckt. Wenn Sie nicht mit Sicherheit annehmen können, dass Ihre Stichprobe aus einer normalverteilten Grundgesamtheit stammt, müssen Sie das Toleranzintervall gemäß der verteilungsfreien Methode verwenden.
Bei der verteilungsfreien Methode wird lediglich vorausgesetzt, dass die Daten stetig sind. Für die verteilungsfreie Methode sind jedoch größere Stichprobenumfänge erforderlich, um genaue Ergebnisse zu erzielen. Wenn Ihr Stichprobenumfang nicht groß genug ist, ist das verteilungsfreie Intervall ein nicht informatives Intervall, das von der negativen Unendlichkeit bis zur Unendlichkeit reicht. In diesem Fall zeigt Minitab ein endliches Intervall auf Grundlage der Spannweite Ihrer Daten an. Daher ist das erreichte Konfidenzniveau viel kleiner als das Soll-Konfidenzniveau.
Interpretation
- Beidseitig
- Verwenden Sie ein beidseitiges Intervall, um das Intervall zu bestimmen, das einen bestimmten Prozentsatz der Messwerte der Grundgesamtheit enthält.
- Obergrenze
- Verwenden Sie eine Obergrenze, um das Intervall zu bestimmen, das angibt, dass ein bestimmter Prozentsatz der Messwerte der Grundgesamtheit nicht größer als eine Obergrenze sein wird.
- Untergrenze
- Verwenden Sie eine Untergrenze, um das Intervall zu bestimmen, das angibt, dass ein bestimmter Prozentsatz der Messwerte der Grundgesamtheit nicht kleiner als eine Untergrenze sein wird.
Erreichte Konfidenz
Bei der verteilungsfreien Methode berechnet Minitab das erreichte Konfidenzniveau. Hierbei handelt es sich um das exakte Konfidenzniveau, das aus der Stichprobe berechnet wurde. Es ist im Allgemeinen größer oder gleich dem Soll-Konfidenzniveau, sofern der Stichprobenumfang nicht zu klein ist.
Interpretation
- Beidseitig
- Verwenden Sie ein beidseitiges Intervall, um das Intervall zu bestimmen, das einen bestimmten Prozentsatz der Messwerte der Grundgesamtheit enthält.
- Obergrenze
- Verwenden Sie eine Obergrenze, um das Intervall zu bestimmen, das angibt, dass ein bestimmter Prozentsatz der Messwerte der Grundgesamtheit nicht größer als eine Obergrenze sein wird.
- Untergrenze
- Verwenden Sie eine Untergrenze, um das Intervall zu bestimmen, das angibt, dass ein bestimmter Prozentsatz der Messwerte der Grundgesamtheit nicht kleiner als eine Untergrenze sein wird.
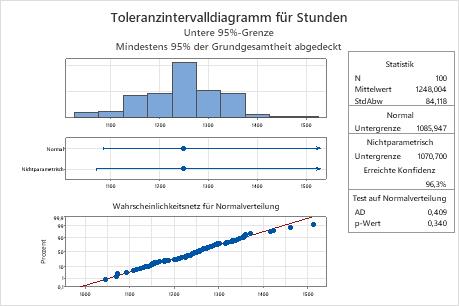
Toleranzintervalldiagramm
- Histogramm: Zeigt die Verteilung der Stichprobendaten. Jeder Balken im Histogramm stellt die Häufigkeit von Daten innerhalb eines Intervalls dar.
- Fehlerbalkendiagramme: Zeigen den Mittelwert und die Obergrenze und/oder Untergrenze des Toleranzintervalls für jede Methode. Eine vertikale Linie am Ende des Intervalls stellt eine Grenze dar. Ein Pfeil gibt an, dass die betreffende Seite des Intervalls keine Grenze aufweist.
- Wahrscheinlichkeitsnetz für Normalverteilung: Zeigt die Güte der Anpassung der Daten an die Normalverteilung. Wenn die Daten normalverteilt sind, dann bilden die Datenpunkte im Wahrscheinlichkeitsnetz eine Gerade.
- Statistiktabelle: Zeigt den Stichprobenumfang, den Mittelwert und die Standardabweichung.
- Tabelle für Normalverteilungsmethode: Zeigt die Obergrenze und/oder Untergrenze des Toleranzintervalls für die Normalverteilungsmethode.
- Tabelle für verteilungsfreie Methode: Zeigt die Obergrenze und/oder Untergrenze des Toleranzintervalls für die verteilungsfreie Methode sowie das erreichte Konfidenzniveau.
- Tabelle für Test auf Normalverteilung: Zeigt den p-Wert und den Wert für den Test auf Normalverteilung nach Anderson-Darling. Um zu ermitteln, ob Sie annehmen können, dass die Daten einer Normalverteilung folgen, vergleichen Sie den p-Wert aus dem Test auf Normalverteilung mit dem Signifikanzniveau (α). Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, können Sie schlussfolgern, dass die Daten keiner Normalverteilung folgen. In diesem Fall müssen Sie das Toleranzintervall gemäß der verteilungsfreien Methode verwenden.
Interpretation
Das Wahrscheinlichkeitsnetz für Normalverteilung zeigt, dass die dargestellten Punkte annähernd eine Gerade bilden, was darauf hinweist, dass die Daten einer Normalverteilung folgen. Darüber hinaus ist der p-Wert für den Test auf Normalverteilung 0,340 und somit größer als das Signifikanzniveau (α = 0,05). Deshalb liegen nicht genügend Anzeichen dafür vor, dass die Daten der Normalverteilung nicht folgen. Der Techniker kann die Ergebnisse der Normalverteilungsmethode verwenden.
Die Untergrenze bei Vorliegen einer Normalverteilung ist 1085,947; daher ist der Techniker zu 95 % sicher, dass mindestens 95 % aller Glühbirnen eine Lebensdauer von ungefähr 1086 Stunden überschreiten. Die mittlere Lebensdauer liegt für alle Glühbirnen bei ungefähr 1248 Stunden, und die Standardabweichung beträgt ungefähr 84,1.