Ein Qualitätstechniker möchte die Lebensdauer der Glühlampen auswerten, die von einem Unternehmen hergestellt werden. Der Techniker entnimmt eine Zufallsstichprobe von 100 Glühlampen und zeichnet deren Lebensdauer bis zum Ausfall auf. Der Techniker möchte die untere Toleranzgrenze berechnen (d. h. die Lebensdauer, die von mindestens 95 % aller Glühlampen überschritten wird).
- Öffnen Sie die Beispieldaten LebensdauerGlühlampen.MWX.
- Wählen Sie aus.
- Wählen Sie in der Dropdownliste die Option Eine oder mehrere Stichproben, jede in einer Spalte aus, und geben Sie Stunden ein.
- Klicken Sie auf Optionen.
- Wählen Sie im Feld Toleranzintervall die Option Untergrenze aus.
- Klicken Sie in den einzelnen Dialogfeldern auf OK.
Interpretieren der Ergebnisse
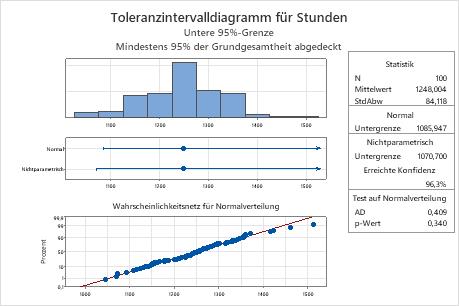
Das Wahrscheinlichkeitsnetz für Normalverteilung zeigt, dass die dargestellten Punkte annähernd eine Gerade bilden, was darauf hinweist, dass die Daten einer Normalverteilung folgen. Darüber hinaus ist der p-Wert für den Test auf Normalverteilung 0,340 und somit größer als das Signifikanzniveau (α = 0,05). Deshalb liegen nicht genügend Anzeichen dafür vor, dass die Daten der Normalverteilung nicht folgen. Der Techniker kann die Ergebnisse der Normalverteilungsmethode verwenden.
Die Untergrenze bei Vorliegen einer Normalverteilung ist 1085,947; daher ist der Techniker zu 95 % sicher, dass mindestens 95 % aller Glühbirnen eine Lebensdauer von ungefähr 1086 Stunden überschreiten. Die mittlere Lebensdauer liegt für alle Glühbirnen bei ungefähr 1248 Stunden, und die Standardabweichung beträgt ungefähr 84,1.
Methode
| Konfidenzniveau | 95% |
|---|---|
| Prozent der Grundgesamtheit in Intervall | 95% |
Statistik
| Variable | N | Mittelwert | StdAbw |
|---|---|---|---|
| Stunden | 100 | 1248,004 | 84,118 |
Untere 95%-Toleranzgrenze
| Variable | Normalverteilungsmethode | Verteilungsfreie Methode | Erreichte Konfidenz |
|---|---|---|---|
| Stunden | 1085,947 | 1070,700 | 96,3% |