In diesem Thema
- Methoden für das Toleranzintervall
- Genaue verteilungsfreie Toleranzintervalle für stetige Verteilungen
- Lognormale Verteilung
- Ungefähre Toleranzintervalle für Gamma-Verteilungen
- Exponentialverteilung
- Verteilung des kleinsten Extremwerts
- Weibull-Verteilung
- Verteilung des größten Extremwerts
- Logistische Verteilung
- Loglogistische Verteilung
- Anderson-Darling-Test
Methoden für das Toleranzintervall
- Lognormal
- Gamma
- Exponential
- Kleinster Extremwert
- Weibull
- Größter Extremwert
- Logistisch
- Loglogistisch
Allgemeine Definitionen
Seien x1, x2, ..., xn die geordneten Statistiken auf der Grundlage einer Zufallsstichprobe mit dem Umfang n aus einer stetigen Verteilung.
Die Verteilungsfunktion sei F(x, θ) für Ω in einem Parameterraum mit einer Dimension größer oder gleich 1.
Seien U < O zwei Statistiken, die auf der Stichprobe basieren, so dass für beliebige gegebene Werte α und P bei 0 < α < 1 und 0 < P < 1 Folgendes für jedes θ in Ω gilt:

Das Intervall [U; O] ist dann ein beidseitiges Toleranzintervall mit dem Inhalt = P x 100 % und dem Konfidenzniveau = 100(1 – α) %. Ein solches Intervall kann als beidseitiges Toleranzintervall (1 – α; P) bezeichnet werden. Wenn beispielsweise α = 0,10 und P = 0,85, wird das resultierende Intervall als beidseitiges Toleranzintervall (90 %; 0,85) bezeichnet.
Wenn U = –∞ und O < +∞, dann wird das Intervall (-∞; O] als einseitige obere Toleranzgrenze (1 – α; P) bezeichnet. Wenn U > -∞ und O = +∞, dann wird das Intervall [U, +∞) als einseitige untere Toleranzgrenze (1 – α; P) bezeichnet.
- Eine einseitige untere Toleranzgrenze (1 – α; P) ist auch eine einseitige obere Toleranzgrenze (P; 1 – α).
- Eine einseitige untere (1 – α)100%-Konfidenzgrenze des (1 – P)-ten Perzentils der Verteilung der Daten ist auch eine einseitige untere Toleranzgrenze (1 – α; P). Ebenso ist eine einseitige obere (1 – α)100%-Konfidenzgrenze des P-ten Perzentils der Verteilung der Daten auch eine einseitige obere Toleranzgrenze (1 – α; P).
- Wenn U und O einseitige untere und obere Toleranzgrenzen (1 – α/2; (1 + P)/2) sind, dann ist [U; O] annähernd ein beidseitiges Toleranzintervall (1 – α; P). Diese Methode kann in Fällen verwendet werden, in denen beidseitige Toleranzintervalle nicht direkt berechnet werden können. Die resultierenden beidseitigen Toleranzintervalle sind im Allgemeinen konservativ. Siehe Guenther1 sowie Hahn und Meeker2.
- Guenther, W. C. (1972). Tolerance intervals for univariate distributions. Naval Research Logistics, 19: 309-333.
- Hahn, G. J. und Meeker, W. Q. (1991). Statistical Intervals: A Guide for Practitioners John Wiley & Sons, New York.
Genaue verteilungsfreie Toleranzintervalle für stetige Verteilungen
Minitab berechnet genaue verteilungsfreie Toleranzintervalle (1 – α; P), wobei 1 – α das Konfidenzniveau und P die Abdeckung ist (der minimale Soll-Prozentsatz der Grundgesamtheit im Intervall). Die verteilungsfreie Methode für Toleranzintervalle ist eine nichtparametrische Methode. Das heißt, verteilungsfreie Toleranzintervalle sind nicht von der übergeordneten Grundgesamtheit der Stichprobe abhängig. Minitab verwendet eine genaue Methode für einseitige und für beidseitige Intervalle.
Seien X 1, X 2 , ... , X n die geordneten Statistiken auf der Grundlage einer Zufallsstichprobe aus einer stetig verteilten Grundgesamtheit F(x;θ). Dann kann auf der Grundlage der Erkenntnisse von Wilks1, 2 und Robbins3 gezeigt werden, dass:

Hierbei ist B die kumulative Verteilungsfunktion der Betaverteilung mit den Parametern a = r und b = n – s + 1. Somit ist (Xr; Xs) ein verteilungsfreies Toleranzintervall, da die Abdeckung des Intervalls eine Betaverteilung mit bekannten Parameterwerten aufweist, die unabhängig von der Verteilung der übergeordneten Grundgesamtheit F(x;θ) sind.
Einseitige Intervalle
Sei k die größte ganze Zahl, die Folgendes erfüllt:

wobei Y eine binomiale Zufallsvariable mit den Parametern n und 1 – P ist. Es kann gezeigt werden (siehe Krishnamoorthy und Mathew4), dass eine einseitige untere Toleranzgrenze (1 – α; P) durch Xk angegeben wird. Entsprechend wird eine einseitige obere Toleranzgrenze (1 – α; P) durch Xn – k +1 angegeben. In beiden Fällen wird die tatsächliche oder effektive Abdeckung als P(Y > k) angegeben.
Beidseitige Intervalle
Sei k die kleinste ganze Zahl, die Folgendes erfüllt:

wobei V eine binomiale Zufallsvariable mit den Parametern n und P ist. Folglich ist:
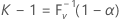
wobei FV–1(x) die inverse kumulative Verteilungsfunktion von V ist. Es kann gezeigt werden (siehe Krishnamoorthy und Mathew4), dass ein beidseitiges Toleranzintervall (1 – α; P) durch (Xr; Xs) angegeben werden kann. Minitab wählt s = n – r + 1 so aus, dass r = (n – k + 1)/2. Sowohl r als auch s werden auf die nächste ganze Zahl abgerundet. Die tatsächliche oder effektive Abdeckung wird als P(V < k – 1) angegeben.
Notation
| Begriff | Beschreibung |
|---|---|
| 1 – α | Konfidenzniveau für das Toleranzintervall |
| P | Abdeckung des Toleranzintervalls (minimaler Soll-Prozentsatz der Grundgesamtheit im Intervall) |
| n | Anzahl der Beobachtungen in der Stichprobe |
- Wilks, S. S. (1941). Sample size for tolerance limits on a normal distribution. The Annals of Mathematical Statistics, 12, 91-96.
- Wilks, S. S. (1941). Statistical prediction with special reference to the problem of tolerance limits. The Annals of Mathematical Statistics, 13, 400–409.
- Robbins, H. (1944). On distribution-free tolerance limits in random sampling. The Annals of Mathematical Statistics, 15, 214-216.
- Krishnamoorthy, K. und Mathew, T. (2009). Statistical Tolerance Regions: Theory, Applications, and Computation. Wiley, Hoboken, NJ.
Lognormale Verteilung
- Minitab ermittelt den natürlichen Logarithmus der Daten.
- Minitab berechnet anhand des Toleranzintervallverfahrens für die Normalverteilung ein Toleranzintervall für die transformierten Daten.
- Minitab potenziert die Grenzen des Toleranzintervalls, die im vorausgegangenen Schritt berechnet wurden, um das Intervall an die Skala der Originaldaten anzupassen.
Ungefähre Toleranzintervalle für Gamma-Verteilungen
Beim Toleranzintervall für die Gamma-Verteilung wird eine Approximation an die Normalverteilung verwendet. Krishnamoorthy et al. führen Simulationsuntersuchungen durch, die zeigen, dass die Approximation genaue Ergebnisse liefert. Die Berechnung wird folgendermaßen durchgeführt:
- Minitab ermittelt die Kubikwurzel der Daten.
- Minitab berechnet anhand des Toleranzintervallverfahrens für die Normalverteilung ein Toleranzintervall für die transformierten Daten.
- Minitab potenziert die Grenzen des Toleranzintervalls, die im vorausgegangenen Schritt berechnet wurden, um das Intervall an die Skala der Originaldaten anzupassen.
- Krishnamoorthy K., Mathew T und Mukherjee S (2008). Normal based methods for a Gamma distribution: prediction and tolerance intervals and stress-strength reliability. Technometrics, 50, 69–78.
Exponentialverteilung
Minitab berechnet genaue Toleranzintervalle (1 – α; P), wobei 1 – α das Konfidenzniveau und P die Abdeckung (der angestrebte Mindestanteil der Bevölkerung im Intervall) ist. Die Formeln für die Berechnung der einseitigen Toleranzgrenzen und der beidseitigen Toleranzintervalle unterscheiden sich.
Einseitige Toleranzgrenzen für die Exponentialverteilung
Diese Formel gibt die Untergrenze an:
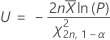
Diese Formel gibt die Obergrenze an:
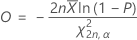
Beidseitige Konfidenzintervalle für die Exponentialverteilung
Minitab verwendet die Newton-Methode zum Lösen des folgenden Gleichungssystems. Weitere Informationen finden Sie in Fernandez1.
Diese Formel gibt das beidseitige Intervall an:

Dabei gilt Folgendes:

, und der Wert hängt von k1 hängt von der Lösung dieses Gleichungssystems ab:

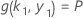
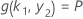
Dabei gilt Folgendes:
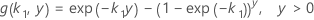
Notation
| Begriff | Beschreibung |
|---|---|
| n | Stichprobenumfang |
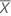 | Mittelwert der Stichprobe |
| P | der angestrebte Mindestanteil der Bevölkerung im Intervall |
 | α-tes Perzentil der Chi-Quadrat-Verteilung mit 2n Freiheitsgraden |
| α | 1 − Konfidenzniveau |
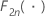 | kumulative Verteilungsfunktion der Chi-Quadrat-Verteilung mit 2n Freiheitsgraden |
- Fernandez, Arturo J. (2010). Two-sided tolerance intervals in the exponential case: Corrigenda and generalizations. Computational Statistics and Data Analysis, 54, 151-162.
Verteilung des kleinsten Extremwerts
Minitab berechnet genaue Toleranzintervalle (1 – α; P) auf der Grundlage von Lawless1, wobei 1 – α das Konfidenzniveau und P die Abdeckung (der minimale Soll-Prozentsatz der Grundgesamtheit im Intervall) ist.
Genaue einseitige Toleranzgrenzen für die Verteilung des kleinsten Extremwerts
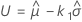
Dabei gilt Folgendes:


mit
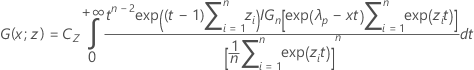
Dabei gilt Folgendes:

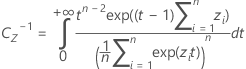
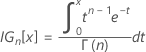
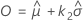
Der Wert von k 2 ergibt sich, wenn in den Formeln für die Berechnung von k 1 der Wert von α durch 1 – α und der Wert von P durch 1 – P ersetzt wird.
Ungefähre beidseitige Toleranzintervalle für die Verteilung des kleinsten Extremwerts
Um das ungefähre beidseitige Intervall zu berechnen, ersetzen Sie in den Formeln für die Berechnung der einseitigen Toleranzgrenzen den Wert von α durch α/2 und den Wert von P durch (P + 1)/2.
Notation
| Begriff | Beschreibung |
|---|---|
 | Maximum-Likelihood-Schätzwert des Lageparameters der Extremwertverteilung |
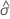 | Maximum-Likelihood-Schätzwert des Skalenparameters der Extremwertverteilung |
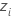 | 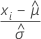 , die zentrierten Beobachtungen auf der Grundlage der MLE-Schätzwerte für den Lage- und den Skalenparameter der Verteilung des kleinsten Extremwerts , die zentrierten Beobachtungen auf der Grundlage der MLE-Schätzwerte für den Lage- und den Skalenparameter der Verteilung des kleinsten Extremwerts |
| t | α-tes Perzentil der nicht zentralen t-Verteilung mit n – 1 Freiheitsgraden und Nichtzentralitätsparameter δP |
| 1 – α | Konfidenzniveau für das Toleranzintervall |
| P | Abdeckung des Toleranzintervalls (minimaler Soll-Prozentsatz der Grundgesamtheit im Intervall) |
| n | Anzahl der Beobachtungen in der Stichprobe |
- Lawless, J. F. (1975). Construction of tolerance bounds for the extreme-value and the Weibull distribution. Technometrics, 17, 255–261.
Weibull-Verteilung
- Minitab ermittelt den natürlichen Logarithmus der Daten.
- Minitab berechnet anhand des Toleranzintervallverfahrens für die Verteilung des kleinsten Extremwerts ein Toleranzintervall für die transformierten Daten.
- Minitab potenziert die Grenzen des Toleranzintervalls, die im vorausgegangenen Schritt berechnet wurden, um das Intervall an die Skala der Originaldaten anzupassen.
Verteilung des größten Extremwerts
- Minitab multipliziert die Daten mit −1.
- Minitab berechnet anhand des Toleranzintervallverfahrens für die Verteilung des kleinsten Extremwerts ein Toleranzintervall für die transformierten Daten.
- Minitab potenziert die Grenzen des Toleranzintervalls, die im vorausgegangenen Schritt berechnet wurden, um das Intervall an die Skala der Originaldaten anzupassen.
Weitere Informationen zu den Formeln, die für die Verteilung des kleinsten Extremwerts verwendet werden, finden Sie im Abschnitt zur Verteilung des kleinsten Extremwerts.
Logistische Verteilung
Minitab berechnet ungefähre Toleranzintervalle (1 − α, P) basierend auf Bain und Engelhardt 1, wobei 1− α das Konfidenzniveau und P die Abdeckung (der angestrebte Mindestprozentsatz der Grundgesamtheit im Intervall) ist. Die Formel für den unteren Toleranzfaktor unterscheidet sich von der Formel für den oberen Toleranzfaktor.
Einseitige Toleranzgrenzen für die logistische Verteilung
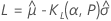
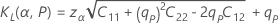
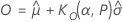

Beidseitige Toleranzgrenzen für die logistische Verteilung
Die Analyse ergibt ein näherungsweises zweiseitiges Toleranzintervall für die logistische Verteilung mit Bonferroni-Ungleichung2. Diese Näherungsmethode ersetzt α durch α/2 und P durch ( P + 1) / 2 in den Formeln zur Berechnung der einseitigen Toleranzgrenzen.
Notation
| Begriff | Beschreibung |
|---|---|
 | der geringere Toleranzfaktor |
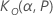 | der obere Toleranzfaktor |
| zα | das obere α Perzentil der Standardnormalverteilung, das dem unteren 1 − α Perzentilpunkt entspricht |
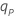 | log(p) − log(1 − p), das p× 100 unteres Perzentil der logistischen Standardverteilung |
| C11 | 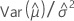 |
| C22 |  |
| C12 | 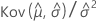 |
 | Maximum-Likelihood-Schätzwert des Lageparameters der logistischen Verteilung |
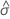 | Maximum-Likelihood-Schätzwert des Skalenparameters der logistischen Verteilung |
- Bain, L. and Englehardt, M. (1991). Statistical analysis of reliability and life testing models: Theory and methods. Second edition, Marcel Dekker, Inc.
- Hahn, G. J. and Meeker, W. Q. (2017). Statistical intervals: A guide for practitioners. Second edition, John Wiley and Sons, Inc.
Loglogistische Verteilung
- Minitab ermittelt den natürlichen Logarithmus der Daten.
- Minitab berechnet anhand des Toleranzintervallverfahrens für die logistische Verteilung ein Toleranzintervall für die transformierten Daten.
- Minitab potenziert die Grenzen des Toleranzintervalls, die im vorausgegangenen Schritt berechnet wurden, um das Intervall an die Skala der Originaldaten anzupassen.
Weitere Informationen zu den Formeln, die für die logistische Verteilung verwendet werden, finden Sie im Abschnitt zur logistischen Verteilung.
Anderson-Darling-Test
Minitab verwendet für den Test auf Güte der Anpassung Anderson-Darling-Statistiken.
Sei Z = F(x), wobei F(x) die kumulative Verteilungsfunktion ist. Angenommen, ein Stichprobe x1, .., xn liefert die Werte Z(i) = F(xi), i=1,.., n. Z(i) wird in der aufsteigenden Reihenfolge Z(1) < Z(2) <...<Z(n) angeordnet. Dann wird die Anderson-Darling-Statistik (A2) wie folgt berechnet:
- A2 = –n – (1/n) Σi[(2i – 1) log Z(i) + (2n + 1 – 2i) log (1 – Z(i))]
Die modifizierte Anderson-Darling-Statistik für den Test auf Güte der Anpassung wird für jede Verteilung berechnet. Die p-Werte beruhen auf der Tabelle von D'Agostino und Stephens.1 Wenn in der Tabelle kein exakter p-Wert gefunden wird, berechnet Minitab den p-Wert durch Interpolation unter Verwendung der Spannweite des p-Werts.
