Wählen Sie die gewünschte Methode oder Formel aus.
Maximum-Likelihood-Schätzwerte
Maximum-Likelihood-Schätzwerte der Verteilungsparameter werden durch Maximieren der Likelihood-Funktion in Bezug auf die Parameter berechnet. Die Maximum-Likelihood-Schätzwerte sind die wahrscheinlichsten Werte der Verteilungsparameter für einen bestimmten Datensatz.
Zum Ermitteln der Maximum-Likelihood-Schätzwerte der Verteilungsparameter wird der Newton-Raphson-Algorithmus verwendet. Der Newton-Raphson-Algorithmus ist eine iterative numerische Methode zum Berechnen des Maximums einer Funktion. 1
Hinweis
Minitab verwendet die Maximum-Likelihood-Methode zum Berechnen der Parameterschätzwerte für alle Verteilungen mit Ausnahme der lognormalen Verteilung. Für die lognormale Verteilung berechnet Minitab erwartungstreue Parameterschätzwerte.
Wahrscheinlichkeitsverteilungen
Lognormale Verteilung
 |
|
| CDF |
 |
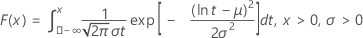| Mittelwert |
 |
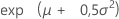| StdAbw |
 |
| Begriff | Beschreibung |
|---|---|
| μ | Skalenparameter |
| σ | Formparameter |
Gamma-Verteilung
 |
|
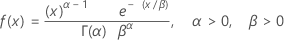| CDF |
 |
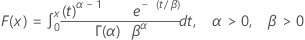| Mittelwert | αβ |
| StdAbw | αβ2 |
| Begriff | Beschreibung |
|---|---|
| α | Formparameter |
| β | Skalenparameter |
Exponentialverteilung
 |
|
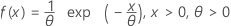| CDF |
 |
| Mittelwert | θ |
| StdAbw | θ |
| Begriff | Beschreibung |
|---|---|
| θ | Skalenparameter |
Verteilung des kleinsten Extremwerts
 |
|
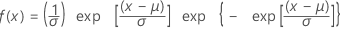| CDF |
 |
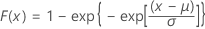| Mittelwert |
 |
| StdAbw |
 |
| Begriff | Beschreibung |
|---|---|
| μ | Lageparameter |
| σ | Skalenparameter |
| γ | Euler-Konstante (ungefähr gleich 0,5772) |
Weibull-Verteilung
 |
|
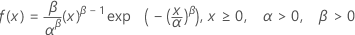| CDF |
 |
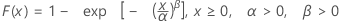| Mittelwert |
 |
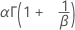| StdAbw |
 |
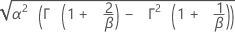| Begriff | Beschreibung |
|---|---|
| α | Skalenparameter |
| β | Formparameter |
Verteilung des größten Extremwerts
 |
|
| CDF |
 |
| Mittelwert |
 |
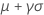| StdAbw |
 |
| Begriff | Beschreibung |
|---|---|
| μ | Lageparameter |
| σ | Skalenparameter |
| γ | Euler-Konstante (ungefähr gleich 0,5772) |
Logistische Verteilung
 |
|
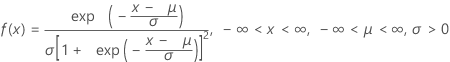| CDF |
 |
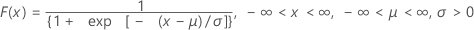| Mittelwert | μ |
| StdAbw |
 |
| Begriff | Beschreibung |
|---|---|
| μ | Lageparameter |
| σ | Skalenparameter |
Loglogistische Verteilung
 |
|
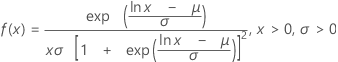| CDF |
 |
| Mittelwert |
 |
| StdAbw |
 |
| Begriff | Beschreibung |
|---|---|
| μ | Lageparameter |
| σ | Skalenparameter |
1 W. Murray, Hrsg. (1972). Numerical Methods for Unconstrained Optimization. Academic Press.
