In diesem Thema
Anzahl von Sequenzen um den Median
Die Anzahl von Sequenzen um den Median ist die Gesamtzahl der Sequenzen über dem Median und die Gesamtzahl der Sequenzen unter dem Median.
Bei einer Sequenz um den Median handelt es sich um einen oder mehrere aufeinander folgende Punkte auf der gleichen Seite der Mittellinie. Eine Sequenz endet, wenn die Linie, die die Punkte verbindet, die Mittellinie überschreitet. Die nächste Sequenz beginnt am nächsten Diagrammpunkt.
Erwartete Anzahl von Sequenzen um den Median
Formel
Die erwartete Anzahl von Sequenzen um den Median beträgt:
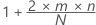
Notation
| Begriff | Beschreibung |
|---|---|
| m | Anzahl der Punkte > Mittellinie |
| n | Anzahl der Punkte ≤ Mittellinie |
| N | Gesamtzahl der Beobachtungen |
Längste Sequenz um den Median
Die Anzahl der Punkte in der längsten Sequenz über oder unter dem Median. Ein Punkt, der auf der Mittellinie liegt, gehört zur Sequenz unter dem Median.
Approx. p-Wert für Cluster
Ein p-Wert kleiner als das angegebene Signifikanzniveau weist auf eine Tendenz zu Clustern hin.
Formel
Unter Annahme einer Standardnormalverteilung ist der p-Wert = cdf(Z).
Dabei gilt Folgendes:
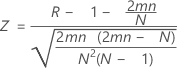
Notation
| Begriff | Beschreibung |
|---|---|
| cdf | kumulative Wahrscheinlichkeit bis Z |
| R | Gesamtzahl der Durchläufe |
| m | Anzahl der Punkte > Mittellinie |
| n | Anzahl der Punkte ≤ Mittellinie |
| N | Gesamtanzahl der Punkte |
Approx. p-Wert für Mischungen
Ein p-Wert kleiner als das angegebene Signifikanzniveau weist auf eine Tendenz zu Mischungen oder Richtungswechseln hin, was wiederum ein Anzeichen dafür sein kann, dass die Daten aus unterschiedlichen Prozessen stammen.
Formel
Unter Annahme einer Standardnormalverteilung ist der p-Wert = 1 – cdf(Z).
Dabei gilt Folgendes:
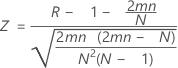
Notation
| Begriff | Beschreibung |
|---|---|
| cdf | kumulative Wahrscheinlichkeit bis Z |
| R | Gesamtzahl der Durchläufe |
| m | Anzahl der Punkte > Mittellinie |
| n | Anzahl der Punkte ≤ Mittellinie |
| N | Gesamtanzahl der Punkte |
Anzahl von ansteigenden/abfallenden Sequenzen
Die Anzahl von ansteigenden/abfallenden Sequenzen ist die Gesamtzahl von aufwärts bzw. abwärts verlaufenden Sequenzen in den Daten.
Eine ansteigende Sequenz ist eine Sequenz aufeinander folgender Punkte, deren Werte ausschließlich ansteigen. Eine abfallende Sequenz ist eine Sequenz aufeinander folgender Punkte, deren Werte ausschließlich abnehmen. Eine Sequenz endet, wenn sich die Richtung (ansteigend oder abfallend) ändert. Wenn z. B. der vorhergehende Wert kleiner ist, beginnt eine ansteigende Sequenz. Diese endet erst, wenn der vorhergehende Wert größer als der nächste Punkt ist. An diesem Punkt beginnt eine abfallende Sequenz.
Erwartete Anzahl von ansteigenden/abfallenden Sequenzen
Formel
Die erwartete Anzahl von ansteigenden/abfallenden Sequenzen beträgt:
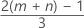
Notation
| Begriff | Beschreibung |
|---|---|
| m | Anzahl der Punkte > Mittellinie |
| n | Anzahl der Punkte ≤ Mittellinie |
Längste ansteigende/abfallende Sequenz
Die Anzahl der Punkte in der längsten ansteigenden oder abfallenden Sequenz.
Approx. p-Wert für Trends
Ein p-Wert kleiner als das angegebene Signifikanzniveau weist auf einen Trend hin.
Formel
Unter Annahme einer Standardnormalverteilung ist der p-Wert = cdf(Z).
Dabei gilt Folgendes:
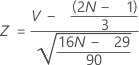
Notation
| Begriff | Beschreibung |
|---|---|
| cdf | kumulative Wahrscheinlichkeit bis Z |
| V | Anzahl von ansteigenden/abfallenden Sequenzen |
| N | Gesamtzahl der Punkte |
Approx. p-Wert für Oszillation
Ein p-Wert kleiner als das angegebene Signifikanzniveau weist auf Oszillation hin.
Formel
Unter Annahme einer Standardnormalverteilung ist der p-Wert = 1 – cdf(Z).
Dabei gilt Folgendes:
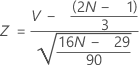
Notation
| Begriff | Beschreibung |
|---|---|
| cdf | kumulative Wahrscheinlichkeit bis Z |
| V | Anzahl von ansteigenden/abfallenden Sequenzen |
| N | Gesamtzahl der Punkte |
