In diesem Thema
Verlaufsdiagramm
In einem Verlaufsdiagramm werden die Prozessdaten in der Reihenfolge dargestellt, in der sie erfasst wurden. Verwenden Sie ein Verlaufsdiagramm, um Muster oder Trends in den Daten zu identifizieren, die auf das Vorhandensein einer Streuung durch Ausnahmebedingungen hinweisen.
Interpretation
Muster in den Daten zeigen an, dass die Streuung auf Ausnahmebedingungen zurückzuführen ist, die untersucht und behoben werden sollten. Die Streuung durch gewöhnliche Ursachen ist jedoch eine Streuung, die einen inhärenten und natürlichen Bestandteil des Prozesses darstellt. Ein Prozess ist stabil, wenn sich nur gewöhnliche Ursachen und keine Ausnahmebedingungen auf die Prozessausgabe auswirken. Wenn in einem Prozess nur gewöhnliche Ursachen für Streuung vorhanden sind, zeigen die Daten ein zufälliges Verhalten.
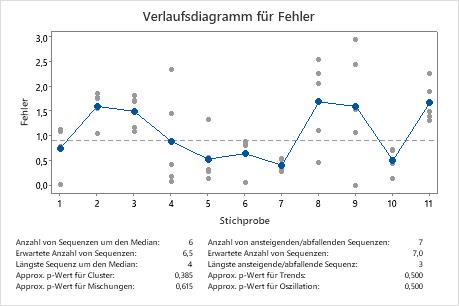
Anzahl von Sequenzen um den Median
Die Anzahl von Sequenzen um den Median ist die Gesamtzahl der Sequenzen über dem Median und die Gesamtzahl der Sequenzen unter dem Median.
Bei einer Sequenz um den Median handelt es sich um einen oder mehrere aufeinander folgende Punkte auf der gleichen Seite der Mittellinie. Eine Sequenz endet, wenn die Linie, die die Punkte verbindet, die Mittellinie überschreitet. Die nächste Sequenz beginnt am nächsten Diagrammpunkt.
Interpretation
- Sequenz 1 umfasst Punkt 1.
- Sequenz 2 umfasst Punkte 2 und 3.
- Sequenz 3 umfasst Punkte 4, 5, 6 und 7.
- Sequenz 4 umfasst Punkte 8 und 9.
- Sequenz 5 umfasst Punkt 10.
- Sequenz 6 umfasst Punkt 11.

Erwartete Anzahl von Sequenzen um den Median
Die erwartete Anzahl von Sequenzen um den Median ist die Anzahl der Sequenzen, die in den Daten erwartet wird, wenn diese zufällig verteilt sind.
Interpretation
Vergleichen Sie die erwartete Anzahl von Sequenzen mit der tatsächlichen Anzahl von Sequenzen. Wenn die Anzahl der Sequenzen höher als erwartet ist, kann dies ein Anzeichen dafür sein, dass die Daten aus zwei Grundgesamtheiten stammen (Mischungen). Weniger Sequenzen als erwartet können auf Cluster in den Daten hindeuten. Verwenden Sie die p-Werte, um die statistische Signifikanz zu ermitteln.

Längste Sequenz um den Median
Die Anzahl der Punkte in der längsten Sequenz über oder unter dem Median. Ein Punkt, der auf der Mittellinie liegt, gehört zur Sequenz unter dem Median.
Interpretation

Approx. p-Wert für Cluster
Der p-Wert ist ein Wahrscheinlichkeitsmaß für die Anzeichen gegen die Annahme der Nullhypothese. Geringere Wahrscheinlichkeiten liefern stärkere Anzeichen dafür, dass die Nullhypothese nicht zutrifft.
Verwenden Sie den p-Wert, um zu bestimmen, ob die Daten zufällig verteilt sind. Die Nullhypothese besagt, dass die Daten zufällig verteilt sind.
Interpretation
Ein p-Wert kleiner als das angegebene Signifikanzniveau weist auf eine Tendenz zu Clustern hin. In der Regel ist ein Signifikanzniveau (als α oder Alpha bezeichnet) von 0,05 gut geeignet. Ein Signifikanzniveau von 0,05 bedeutet ein Risiko von 5 %, dass auf ein nicht zufälliges Muster geschlossen wird, während die Daten tatsächlich zufällig verteilt sind.
- p-Wert ≤ α: Die Differenzen zwischen den Mittelwerten unterschieden sich signifikant (H0 verwerfen)
- Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, weisen Sie die Nullhypothese zurück. Sie können schlussfolgern, dass die Daten nicht zufällig verteilt sind.
- p-Wert > α: Die Differenzen zwischen den Mittelwerten unterscheiden sich nicht signifikant (H0 nicht verwerfen)
- Wenn der p-Wert größer als das Signifikanzniveau ist, weisen Sie die Nullhypothese nicht zurück. Es liegen nicht genügend Anzeichen für die Schlussfolgerung vor, dass die Daten nicht zufällige Muster aufweisen. Sie können jedoch auch nicht schlussfolgern, dass die Daten zufällig verteilt sind.

Approx. p-Wert für Mischungen
Der p-Wert ist ein Wahrscheinlichkeitsmaß für die Anzeichen gegen die Annahme der Nullhypothese. Geringere Wahrscheinlichkeiten liefern stärkere Anzeichen dafür, dass die Nullhypothese nicht zutrifft.
Verwenden Sie den p-Wert, um zu bestimmen, ob die Daten zufällig verteilt sind. Die Nullhypothese besagt, dass die Daten zufällig verteilt sind.
Interpretation
Ein p-Wert kleiner als das angegebene Signifikanzniveau weist auf eine Tendenz zu Mischungen hin. In der Regel ist ein Signifikanzniveau (als α oder Alpha bezeichnet) von 0,05 gut geeignet. Ein Signifikanzniveau von 0,05 bedeutet ein Risiko von 5 %, dass auf ein nicht zufälliges Muster geschlossen wird, während die Daten tatsächlich zufällig verteilt sind.
- p-Wert ≤ α: Die Differenzen zwischen den Mittelwerten unterschieden sich signifikant (H0 verwerfen)
- Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, weisen Sie die Nullhypothese zurück. Sie können schlussfolgern, dass die Daten nicht zufällig verteilt sind.
- p-Wert > α: Die Differenzen zwischen den Mittelwerten unterscheiden sich nicht signifikant (H0 nicht verwerfen)
- Wenn der p-Wert größer als das Signifikanzniveau ist, weisen Sie die Nullhypothese nicht zurück. Es liegen nicht genügend Anzeichen für die Schlussfolgerung vor, dass die Daten nicht zufällige Muster aufweisen. Sie können jedoch auch nicht schlussfolgern, dass die Daten zufällig verteilt sind.

Anzahl von ansteigenden/abfallenden Sequenzen
Die Anzahl von ansteigenden/abfallenden Sequenzen ist die Gesamtzahl von aufwärts bzw. abwärts verlaufenden Sequenzen in den Daten.
Eine ansteigende Sequenz ist eine Sequenz aufeinander folgender Punkte, deren Werte ausschließlich ansteigen. Eine abfallende Sequenz ist eine Sequenz aufeinander folgender Punkte, deren Werte ausschließlich abnehmen. Eine Sequenz endet, wenn sich die Richtung (ansteigend oder abfallend) ändert. Wenn z. B. der vorhergehende Wert kleiner ist, beginnt eine ansteigende Sequenz. Diese endet erst, wenn der vorhergehende Wert größer als der nächste Punkt ist. An diesem Punkt beginnt eine abfallende Sequenz.
Minitab zählt eine flache Sequenz von aufeinander folgenden gleichen Beobachtungen als Teil einer abfallenden Sequenz.
Interpretation
- Punkt 2 kennzeichnet das Ende von Sequenz 1.
- Punkt 5 kennzeichnet das Ende von Sequenz 2.
- Punkt 6 kennzeichnet das Ende von Sequenz 3.
- Punkt 7 kennzeichnet das Ende von Sequenz 4.
- Punkt 8 kennzeichnet das Ende von Sequenz 5.
- Punkt 10 kennzeichnet das Ende von Sequenz 6.
- Punkt 11 kennzeichnet das Ende von Sequenz 7.

Interpretieren einer flachen Sequenz
3 ansteigende und abfallende Sequenzen
1 abfallende Sequenz
Erwartete Anzahl von ansteigenden/abfallenden Sequenzen
Die erwartete Anzahl von ansteigenden/abfallenden Sequenzen ist die Anzahl der Sequenzen, die in den Daten erwartet wird, wenn diese zufällig verteilt sind.
Interpretation
Vergleichen Sie die erwartete Anzahl von Sequenzen mit der tatsächlichen Anzahl von Sequenzen. Mehr Sequenzen als erwartet können auf Oszillation in den Daten hindeuten. Weniger Sequenzen als erwartet können auf einen Trend in den Daten hindeuten. Verwenden Sie die p-Werte, um die Signifikanz zu ermitteln.

Längste ansteigende/abfallende Sequenz
Die Anzahl der Punkte in der längsten ansteigenden oder abfallenden Sequenz.
Interpretation

Approx. p-Wert für Trends
Der p-Wert ist ein Wahrscheinlichkeitsmaß für die Anzeichen gegen die Annahme der Nullhypothese. Geringere Wahrscheinlichkeiten liefern stärkere Anzeichen dafür, dass die Nullhypothese nicht zutrifft.
Verwenden Sie den p-Wert, um zu bestimmen, ob die Daten zufällig verteilt sind. Die Nullhypothese besagt, dass die Daten zufällig verteilt sind.
Interpretation
Ein p-Wert kleiner als das angegebene Signifikanzniveau weist auf eine Tendenz zu Trends hin. In der Regel ist ein Signifikanzniveau (als α oder Alpha bezeichnet) von 0,05 gut geeignet. Ein Signifikanzniveau von 0,05 bedeutet ein Risiko von 5 %, dass auf ein nicht zufälliges Muster geschlossen wird, während die Daten tatsächlich zufällig verteilt sind.
- p-Wert ≤ α: Die Differenzen zwischen den Mittelwerten unterschieden sich signifikant (H0 verwerfen)
- Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, weisen Sie die Nullhypothese zurück. Sie können schlussfolgern, dass die Daten nicht zufällig verteilt sind.
- p-Wert > α: Die Differenzen zwischen den Mittelwerten unterscheiden sich nicht signifikant (H0 nicht verwerfen)
- Wenn der p-Wert größer als das Signifikanzniveau ist, weisen Sie die Nullhypothese nicht zurück. Es liegen nicht genügend Anzeichen für die Schlussfolgerung vor, dass die Daten nicht zufällige Muster aufweisen. Sie können jedoch auch nicht schlussfolgern, dass die Daten zufällig verteilt sind.

Approx. p-Wert für Oszillation
Der p-Wert ist ein Wahrscheinlichkeitsmaß für die Anzeichen gegen die Annahme der Nullhypothese. Geringere Wahrscheinlichkeiten liefern stärkere Anzeichen dafür, dass die Nullhypothese nicht zutrifft.
Verwenden Sie den p-Wert, um zu bestimmen, ob die Daten zufällig verteilt sind. Die Nullhypothese besagt, dass die Daten zufällig verteilt sind.
Interpretation
Ein p-Wert kleiner als das angegebene Signifikanzniveau weist auf eine Tendenz zu Oszillation hin. In der Regel ist ein Signifikanzniveau (als α oder Alpha bezeichnet) von 0,05 gut geeignet. Ein Signifikanzniveau von 0,05 bedeutet ein Risiko von 5 %, dass auf ein nicht zufälliges Muster geschlossen wird, während die Daten tatsächlich zufällig verteilt sind.
- p-Wert ≤ α: Die Differenzen zwischen den Mittelwerten unterschieden sich signifikant (H0 verwerfen)
- Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, weisen Sie die Nullhypothese zurück. Sie können schlussfolgern, dass die Daten nicht zufällig verteilt sind.
- p-Wert > α: Die Differenzen zwischen den Mittelwerten unterscheiden sich nicht signifikant (H0 nicht verwerfen)
- Wenn der p-Wert größer als das Signifikanzniveau ist, weisen Sie die Nullhypothese nicht zurück. Es liegen nicht genügend Anzeichen für die Schlussfolgerung vor, dass die Daten nicht zufällige Muster aufweisen. Sie können jedoch auch nicht schlussfolgern, dass die Daten zufällig verteilt sind.

