In diesem Thema
Schritt 1: Anpassung der Normalverteilung untersuchen
Verwenden Sie die Wahrscheinlichkeitsnetze für Normalverteilung, um zu beurteilen, wie eng die Original- und die transformierten Daten der Normalverteilung folgen.
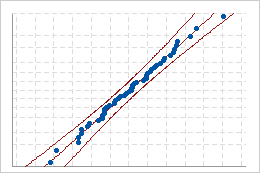
Gute Anpassung
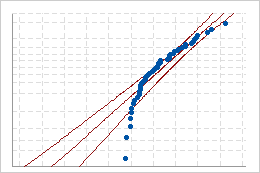
Schlechte Anpassung
Hinweis
Wenn die Originaldaten normalverteilt sind, zeigt Minitab nur ein einzelnes Wahrscheinlichkeitsnetz an und führt die Johnson-Transformation nicht durch.
Schritt 2: Anpassung der Normalverteilung auswerten
Verwenden Sie den p-Wert, um zu beurteilen, ob Sie annehmen können, dass die Original- und die transformierten Daten der Normalverteilung folgen.
- Ein p-Wert kleiner als Alpha deutet darauf hin, dass die Normalverteilung keine gute Anpassung darstellt.
- Ein p-Wert größer oder gleich Alpha deutet darauf hin, dass nicht genügend Anzeichen für eine schlechte Verteilungsanpassung vorliegen. Sie können annehmen, dass die Daten der Normalverteilung folgen.
Wenn die Johnson-Transformation wirksam ist, ist der p-Wert für die transformierten Daten größer als Alpha.
Wichtig
Seien Sie beim Interpretieren von Ergebnissen, die aus sehr kleinen oder sehr großen Stichproben stammen, vorsichtig. Bei einer sehr kleinen Stichprobe besitzt ein Test der Anpassungsgüte möglicherweise nicht die erforderliche Trennschärfe, um signifikante Abweichungen von der Verteilung zu erkennen. Bei einer sehr großen Stichprobe hingegen ist die Trennschärfe so groß, dass auch kleine Abweichungen von der Verteilung erkannt werden, die keine praktische Bedeutung besitzen. Verwenden Sie zusätzlich zu den p-Werten die Wahrscheinlichkeitsnetze, um die Verteilungsanpassung zu beurteilen.
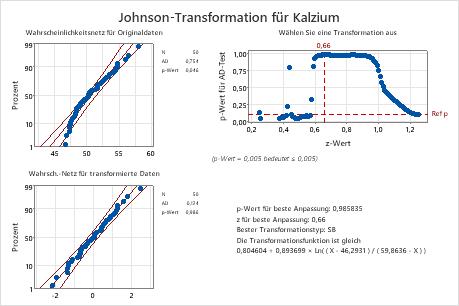
Wichtigstes Ergebnis: p-Wert
In diesen Ergebnissen ist der p-Wert (0,046) für die Originaldaten kleiner als Alpha (0,10), was darauf hinweist, dass die ursprünglichen Kalziumdaten nicht normalverteilt sind. Für die transformierten Daten ist der p-Wert (0,986) größer als Alpha. Daher können Sie annehmen, dass die transformierten Daten einer Normalverteilung folgen.
Schritt 3: Transformationsfunktion untersuchen
Minitab zeigt die Parameter der Johnson-Transformationsfunktion an, die die beste Anpassung ergibt. Minitab verwendet diese Funktion, um die ursprünglichen Daten zu transformieren.
Angenommen, die Johnson-Transformationsfunktion lautet 0,762475 + 0,870902 × Ln((x – 46,3174 )/(59,6770 – x)). Wenn der ursprüngliche Datenwert für x gleich 50 ist, wird der transformierte Datenwert für 50 wie folgt berechnet: 0,762475 + 0,870902 × Ln((50 – 46,3174)/(59,677 – 50)), was –0,07893 ergibt.
Hinweis
Um alle transformierten Datenwerte im Arbeitsblatt zu speichern, geben Sie beim Durchführen der Analyse eine Speicherspalte ein.
Weitere Informationen zum Algorithmus, mit dem Minitab die Johnson-Transformationsfunktion ermittelt, finden Sie unter Methoden und Formeln für Transformationen in Identifikation der Verteilung; klicken Sie dort auf „Methoden und Formeln für die Johnson-Transformation“.
