In diesem Thema
Wahrscheinlichkeitsnetz für Originaldaten und transformierte Daten
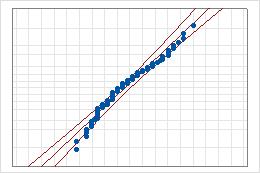
- Mittellinie
- Das erwartete Perzentil aus der Verteilung auf der Grundlage der geschätzten Maximum-Likelihood-Parameter.
- Linien der Konfidenzgrenzen
- Eine gekrümmte Linie links bildet die Untergrenzen der Konfidenzintervalle für die Perzentile ab. Eine gekrümmte Linie rechts bildet die Obergrenzen der Konfidenzintervalle für die Perzentile ab.
Interpretation
Verwenden Sie die Wahrscheinlichkeitsnetze für Normalverteilung, um zu beurteilen, wie eng die Original- und die transformierten Daten der Normalverteilung folgen.
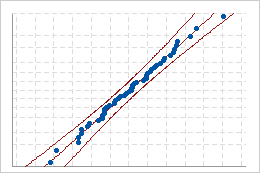
Gute Anpassung
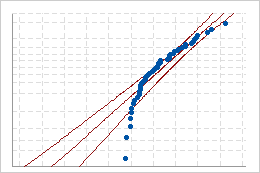
Schlechte Anpassung
Hinweis
Wenn die Originaldaten normalverteilt sind, zeigt Minitab nur ein einzelnes Wahrscheinlichkeitsnetz an und führt die Johnson-Transformation nicht durch.
N
Die Anzahl der nicht fehlenden Werte in der Stichprobe. N ist die Anzahl aller beobachteten Werte.
| Gesamt | N | N* |
|---|---|---|
| 149 | 141 | 8 |
Interpretation
Verwenden Sie N, um den Umfang der Stichprobe festzustellen.
Wichtig
Seien Sie beim Interpretieren von Ergebnissen, die aus sehr kleinen oder sehr großen Stichproben stammen, vorsichtig. Bei einer sehr kleinen Stichprobe besitzt ein Test der Anpassungsgüte möglicherweise nicht die erforderliche Trennschärfe, um signifikante Abweichungen von der Verteilung zu erkennen. Bei einer sehr großen Stichprobe hingegen ist die Trennschärfe so groß, dass auch kleine Abweichungen von der Verteilung erkannt werden, die keine praktische Bedeutung besitzen. Verwenden Sie zusätzlich zu den p-Werten die Wahrscheinlichkeitsnetze, um die Verteilungsanpassung zu beurteilen.
AD
Die Statistik zur Güte der Anpassung nach Anderson-Darling (AD) ist ein Maß für die Abweichungen zwischen der Anpassungslinie (basierend auf der ausgewählten Verteilung) und der verteilungsfreien Treppenfunktion (basierend auf den Datenpunkten). Die Anderson-Darling-Statistik ist eine quadrierte Distanz, die in den Randbereichen der Verteilung stärker gewichtet ist.
Interpretation
Minitab verwendet die Anderson-Darling-Statistik, um den p-Wert zu berechnen. Der p-Wert ist eine Wahrscheinlichkeit, mit der die Anzeichen gegen die Annahme der Nullhypothese gemessen werden, dass die Daten der Verteilung folgen.
Im Allgemeinen weisen deutlich kleinere Werte für die Anderson-Darling-Statistik darauf hin, dass die Daten einer Verteilung enger folgen. Wenn die AD-Werte für verschiedene Verteilungen nahe beieinander liegen, sollten Sie diese jedoch nicht direkt vergleichen, da die AD-Statistiken für verschiedene Verteilungen unterschiedlich verteilt sind. Um die Anpassung verschiedener Verteilungen besser vergleichen zu können, sollten Sie weitere Kriterien verwenden, zum Beispiel die Wahrscheinlichkeitsnetze, die p-Werte und Ihre Kenntnisse des Prozesses.
p-Wert
Minitab gibt einen p-Wert für den Anderson-Darling-Test auf Normalverteilung (AD) für die Originaldatenwerte und die transformierten Datenwerte aus. Der p-Wert ist ein Wahrscheinlichkeitsmaß für die Anzeichen gegen die Annahme der Nullhypothese. Für einen AD-Test auf Normalverteilung besagt die Nullhypothese, dass die Daten der Normalverteilung folgen. Daher bieten kleinere p-Werte deutlichere Anzeichen dafür, dass die Daten der Normalverteilung nicht folgen.
Interpretation
Verwenden Sie den p-Wert, um zu beurteilen, ob die Original- und die transformierten Daten der Normalverteilung folgen. Ein größerer p-Wert weist in der Regel auf eine bessere Anpassung an die Daten hin.
- Ein p-Wert kleiner als Alpha deutet darauf hin, dass die Normalverteilung keine gute Anpassung darstellt.
- Ein p-Wert größer oder gleich Alpha deutet darauf hin, dass nicht genügend Anzeichen für eine schlechte Verteilungsanpassung vorliegen. Sie können annehmen, dass die Daten der Normalverteilung folgen.
Wenn die Johnson-Transformation wirksam ist, ist der p-Wert für die transformierten Daten größer als Alpha.
Wichtig
Seien Sie beim Interpretieren von Ergebnissen, die aus sehr kleinen oder sehr großen Stichproben stammen, vorsichtig. Bei einer sehr kleinen Stichprobe besitzt ein Test der Anpassungsgüte möglicherweise nicht die erforderliche Trennschärfe, um signifikante Abweichungen von der Verteilung zu erkennen. Bei einer sehr großen Stichprobe hingegen ist die Trennschärfe so groß, dass auch kleine Abweichungen von der Verteilung erkannt werden, die keine praktische Bedeutung besitzen. Verwenden Sie zusätzlich zu den p-Werten die Wahrscheinlichkeitsnetze, um die Verteilungsanpassung zu beurteilen.
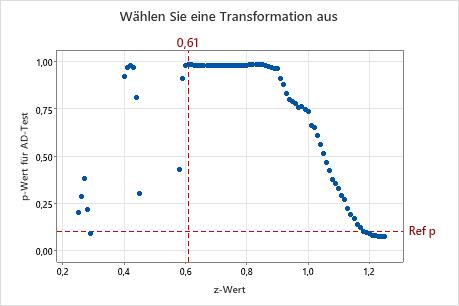
Grafik „Wählen Sie eine Transformation aus“
In der Grafik „Wählen Sie eine Transformation aus“ wird der berechnete p-Wert des AD-Tests auf Normalverteilung für jeden Z-Wert für verschiedene Johnson-Transformationsfunktionen dargestellt. Bei der Johnson-Transformation wird ein Gitter von Z-Werten im Bereich von 0,25 bis 1,25 in Schritten von 0,01 für eine Reihe von Verteilungen verwendet, um den optimalen Z-Wert zu ermitteln. Minitab berechnet den p-Wert der transformierten Daten für jeden Z-Wert und wählt eine Transformationsfunktion mit dem größten p-Wert aus, der größer als der für die Analyse angegebene p-Wert ist.
Interpretation
Verwenden Sie die Grafik „Wählen Sie eine Transformation aus“, um zu visualisieren, wie die Johnson-Transformationsfunktion ausgewählt wird, um die beste Anpassung an die Daten zu erzielen. Die horizontale Referenzlinie zeigt den für die Analyse angegebenen p-Wert. Die vertikale Referenzlinie zeigt den Z-Wert für die Transformation, die die beste Anpassung ergibt. Dieser Z-Maximalwert entspricht dem p-Mindestwert für den AD-Test auf Normalverteilung.
Hinweis
In der Tabelle unter der Grafik (hier nicht gezeigt) werden die Parameterschätzwerte für die beste Transformationsfunktion aufgeführt. Weitere Informationen zum Algorithmus, mit dem Minitab die Johnson-Transformationsfunktion ermittelt, finden Sie unter Methoden und Formeln für Transformationen in Identifikation der Verteilung; klicken Sie dort auf „Methoden und Formeln für die Johnson-Transformation“.
p-Wert für beste Anpassung
Der p-Wert für beste Anpassung gibt den p-Wert für die Johnson-Transformationsfunktion an, bei der die transformierten Daten am besten an die Normalverteilung angepasst sind. Dieser auf das nächste Tausendstel gerundete p-Wert wird auch im Wahrscheinlichkeitsnetz für die transformierten Daten angezeigt.
Informationen zum Interpretieren des p-Werts finden Sie im Abschnitt zum p-Wert.
Informationen dazu, wie Minitab die Johnson-Transformationsfunktion mit der besten Anpassung auswählt, finden Sie im Abschnitt zur Grafik „Wählen Sie eine Transformation aus“.
z für beste Anpassung
Der z-Wert für die beste Anpassung gibt den z-Wert für die Johnson-Transformationsfunktion an, bei der die transformierten Daten am besten an die Normalverteilung angepasst sind. Der optimale z-Wert entspricht dem p-Wert für die beste Anpassung, wie in der Grafik für die beste Transformation gezeigt.
Informationen dazu, wie Minitab den z-Wert zur Auswahl der Johnson-Transformationsfunktion mit der besten Anpassung verwendet, finden Sie im Abschnitt über die Grafik „Wählen Sie eine Transformation aus“.
Bester Transformationstyp
Die Johnson-Transformation wählt eine der drei Verteilungsfamilien: SB, SL und SU, wobei B, L und U sich entsprechend auf die Variable beziehen: begrenzt, lognormal bzw. unbegrenzt. Minitab verwendet die gewählte Verteilungsfunktion, um die Daten zu transformieren, damit sie einer Normalverteilung folgen.
Weitere Informationen zum Algorithmus, mit dem Minitab die Johnson-Transformationsfunktion ermittelt, finden Sie unter Methoden und Formeln für Transformationen in Identifikation der Verteilung; klicken Sie dort auf „Methoden und Formeln für die Johnson-Transformation“.
Johnson-Transformationsfunktion
Minitab zeigt die Parameter der Johnson-Transformationsfunktion an, die die beste Anpassung ergibt. Minitab verwendet diese Funktion, um die ursprünglichen Daten zu transformieren.
Angenommen, die Johnson-Transformationsfunktion lautet 0,762475 + 0,870902 × Ln((x – 46,3174)/(59,6770 – X)). Wenn der ursprüngliche Datenwert für x gleich 50 ist, wird der transformierte Datenwert für 50 wie folgt berechnet: 0,762475 + 0,870902 × Ln((50 – 46,3174)/(59,6770 – 50)), was –0,07893 ergibt.
Hinweis
Um alle transformierten Werte im Arbeitsblatt zu speichern, geben Sie beim Durchführen der Analyse eine Speicherspalte ein.
Weitere Informationen zum Algorithmus, mit dem Minitab die Johnson-Transformationsfunktion ermittelt, finden Sie unter Methoden und Formeln für Transformationen in Identifikation der Verteilung; klicken Sie dort auf „Methoden und Formeln für die Johnson-Transformation“.
