Ein Qualitätstechniker für einen Hersteller von Nahrungsmittelzusätzen möchten den Kalziumgehalt in Vitaminkapseln auswerten. Er erfasst eine Zufallsstichprobe von Kapseln und zeichnet deren Kalziumgehalt auf. Aufgrund früherer Erfahrungen ist dem Techniker bekannt, dass die Daten rechtsschief sind.
Der Techniker führt eine Johnson-Transformation durch, um die Daten so zu transformieren, dass sie einer Normalverteilung folgen, und die transformierten Werte für die weitere Analyse im Arbeitsblatt zu speichern.
- Öffnen Sie die Beispieldaten Kalziumgehalt.MWX.
- Wählen Sie aus.
- Wählen Sie im Feld Anordnung der Daten die Option Einzelne Spalte aus, und geben Sie dann Kalzium ein.
- Geben Sie unter Transformierte Daten speichern in im Feld Einzelne Spalte den Wert C2 ein.
- Klicken Sie auf OK.
Interpretieren der Ergebnisse
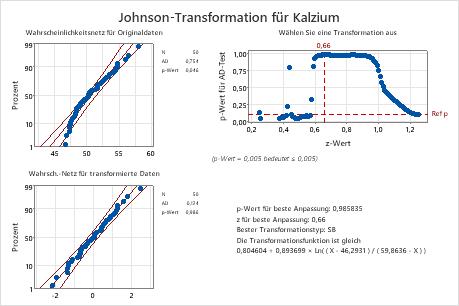
Minitab zeigt ein Wahrscheinlichkeitsnetz für Normalverteilung und einen p-Wert für die Originaldaten und die transformierten Daten an. Wenn die Daten normalverteilt sind, folgten die Punkte im Diagramm einer annähernden Geraden, und der p-Wert ist größer als das Alpha-Niveau. Um die Verteilungsanpassung zu beurteilen, wird häufig ein Alpha-Niveau von 0,05 oder 0,10 verwendet.
Bei den Originaldaten folgen die Datenpunkte im Wahrscheinlichkeitsnetz keiner Geraden, und der p-Wert (0,046) ist kleiner als Alpha; dies weist darauf hin, dass die ursprünglichen Kalziumdaten nicht normalverteilt sind. Bei den transformierten Daten liegen die Datenpunkte im Wahrscheinlichkeitsnetz entlang der Geraden, und der p-Wert (0,986) ist größer als Alpha. Daher können Sie annehmen, dass die transformierten Kalziumdaten einer Normalverteilung folgen.