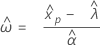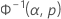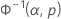In diesem Thema
Wahrscheinlichkeitsnetz
Das Wahrscheinlichkeitsnetz besteht aus folgenden Elementen:
- Punkte: Die geschätzten Perzentile für die entsprechenden Wahrscheinlichkeiten eines geordneten Datensatzes.
- Mittellinie: Die erwarteten Perzentile aus der Verteilung auf der Grundlage der geschätzten Maximum-Likelihood-Parameter. Wenn die Verteilung gut an die Daten angepasst ist, sind die Punkte entlang der Mittellinie angeordnet.
Geschätzte Wahrscheinlichkeiten
Minitab schätzt die Wahrscheinlichkeit (P), die verwendet wird, um die Diagrammpunkte zu berechnen, mit den folgenden Methoden.
- Median-Rang (Benard-Methode)
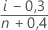
- Mittlerer Rang (Herd-Johnson-Schätzung)

- Kaplan-Meier modifiziert (Hazen)
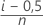
- Kaplan-Meier-Produktlimitschätzung

Notation
| Begriff | Beschreibung |
|---|---|
| n | Anzahl der Beobachtungen |
| i | Rang der i-ten geordneten Beobachtung x(i), wobei x(1), x(2),...x(n) die Reihenfolgestatistiken oder die vom kleinsten zum größten Wert sortierten Daten sind |
Diagrammpunkte
Die Mittellinie des Wahrscheinlichkeitsnetzes wird mit Hilfe der Berechnungen für die x- und y-Koordinate in dieser Tabelle erstellt.
| Verteilung | x-Koordinate | y-Koordinate |
|---|---|---|
| Kleinster Extremwert | x | ln(–ln(1 – p)) |
| Größter Extremwert | x | ln(–ln p) |
| Weibull | ln(x) | ln(–ln(1 – p)) |
| Weibull mit 3 Parametern | ln(x – Schwellenwert) | ln(–ln(1 – p)) |
| Exponential | ln(x) | ln(–ln(1 – p)) |
| Exponential mit 2 Parametern | ln(x – Schwellenwert) | ln(–ln(1 – p)) |
| Normal | x | Φ–1norm |
| Lognormal | ln(x) | Φ–1norm |
| Lognormal mit 3 Parametern | ln(x – Schwellenwert) | Φ–1norm |
| Logistisch | x |
 |
| Loglogistisch | ln(x) |
 |
| Loglogistisch mit 3 Parametern | ln(x – Schwellenwert) |
 |
| Gamma | x | Φ–1Gamma |
| Gamma mit 3 Parametern | ln(x – Schwellenwert) | Φ–1Gamma |
Hinweis
Da die Diagrammpunkte von keiner Verteilung abhängig sind, sind sie vor der Transformation für jedes Wahrscheinlichkeitsnetz gleich. Die Anpassungslinie unterscheidet sich jedoch je nach ausgewählter Verteilung.
Notation
| Begriff | Beschreibung |
|---|---|
| p | Geschätzte Wahrscheinlichkeit |
| Φ-1norm | Der für p von der inversen Verteilungsfunktion der Standardnormalverteilung zurückgegebene Wert |
| Φ-1Gamma | Der für p von der inversen Verteilungsfunktion der unvollständigen Gamma-Verteilung zurückgegebene Wert |
| ln(x) | Natürlicher Logarithmus von x |
Perzentile und Standardfehler der Perzentile
Ein Perzentil ist ein Wert auf einer Skala von 0 bis 100, der den prozentualen Anteil einer Verteilung angibt, der kleiner oder gleich diesem Wert ist. Standardmäßig zeigt Minitab in der verteilungsgebundenen Analyse Perzentiltabellen für gängige Perzentile an.
Die Standardfehler für die geschätzten Perzentile sind die Quadratwurzeln der Varianzen.
 ,
,  ,
,  ,
,  ,
,  ,
, 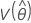 ,
, 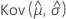 ,
, 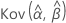 und
und 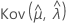 geben die Varianzen und Kovarianzen der MLEs von μ, σ, α, β, λ und θ an, die aus dem entsprechenden Element der Inverse der Fisher-Informationsmatrix entnommen wurden.
geben die Varianzen und Kovarianzen der MLEs von μ, σ, α, β, λ und θ an, die aus dem entsprechenden Element der Inverse der Fisher-Informationsmatrix entnommen wurden.
Die für die Schätzwerte der Perzentile und Varianzen verwendeten Formeln lauten wie folgt:
Verteilung des kleinsten Extremwerts
- Perzentil
-
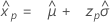
- Varianz
-

Verteilung des größten Extremwerts
- Perzentil
-
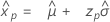
- Varianz
-

Weibull-Verteilung
- Perzentil
-

- Varianz
-
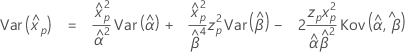
Weibull-Verteilung mit 3 Parametern
- Perzentil
-
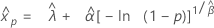
- Varianz
-
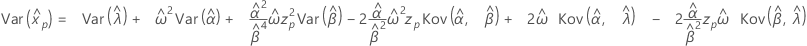
Exponentialverteilung
- Perzentil
-

- Varianz
-

Exponentialverteilung mit 2 Parametern
- Perzentil
-
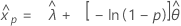
- Varianz
-

Normalverteilung
- Perzentil
-
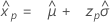
- Varianz
-

Lognormale Verteilung
- Perzentil
-

- Varianz
-

Lognormalverteilung mit 3 Parametern
- Perzentil
-

- Varianz
-
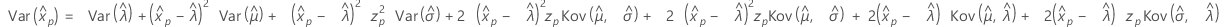
Logistische Verteilung
- Perzentil
-
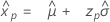
- Varianz
-

Loglogistische Verteilung
- Perzentil
-

- Varianz
-

Loglogistische Verteilung mit 3 Parametern
- Perzentil
-

- Varianz
-
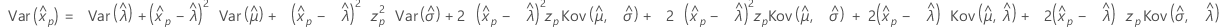
Gamma-Verteilung
- Perzentil
-
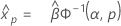
- Varianz
-
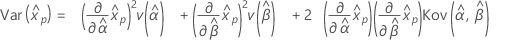
Gamma-Verteilung mit 3 Parametern
- Perzentil
-
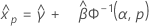
- Varianz
-
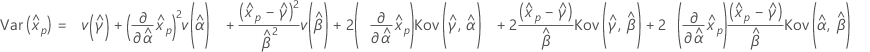
Konfidenzgrenzen für Perzentile
| Verteilung | Konfidenzgrenzen |
|---|---|
| Kleinster Extremwert |
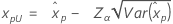 |
| Größter Extremwert |
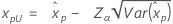 |
| Normal |
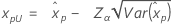 |
| Logistisch |
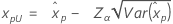 |
| Weibull |
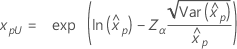 |
| Exponential |
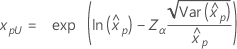 |
| Lognormal |
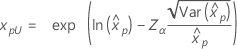 |
| Loglogistisch |
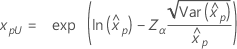 |
| Weibull mit 3 Parametern |
Wenn λ < 0:
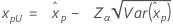 Wenn λ ≥ 0:
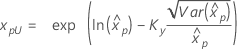 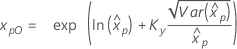 |
| Exponential mit 2 Parametern |
Wenn λ < 0:
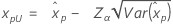 Wenn λ ≥ 0:
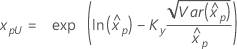 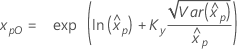 |
| Lognormal mit 3 Parametern |
Wenn λ < 0:
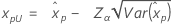 Wenn λ ≥ 0:
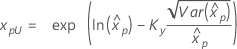 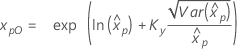 |
| Loglogistisch mit 3 Parametern |
Wenn λ < 0:
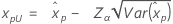 Wenn λ ≥ 0:
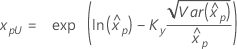 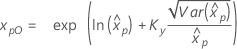 |
Notation
| Begriff | Beschreibung |
|---|---|
| Kγ | (1 + γ)/2-tes Perzentil einer Standardnormalverteilung |