In diesem Thema
Schritt 1: Anpassung der Normalverteilung untersuchen
Verwenden Sie das Wahrscheinlichkeitsnetz, um zu ermitteln, wie eng die Daten jeder Verteilung folgen.
Wenn die Verteilung gut an die Daten angepasst ist, sollten die Punkte eng um die angepasste Verteilungslinie liegen. Abweichungen von der Geraden weisen darauf hin, dass die Anpassung nicht akzeptabel ist.
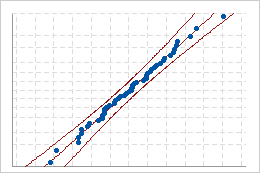
Gute Anpassung
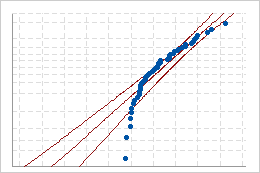
Schlechte Anpassung
Verwenden Sie neben den Wahrscheinlichkeitsnetzen die Maße zur Anpassungsgüte, z. B. die p-Werte, und nutzen Sie Ihre praktischen Prozesskenntnisse, um die Anpassung der Verteilung zu beurteilen.
Schritt 2: Anpassung der Verteilung auswerten
Verwenden Sie den p-Wert, um die Anpassung der Verteilung zu beurteilen.
- P ≤ α: Die Daten folgen der Verteilung nicht (H0 verwerfen)
- Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, weisen Sie die Nullhypothese zurück und schlussfolgern, dass die Daten der Verteilung nicht folgen.
- P > α: Es kann nicht gefolgert werden, dass die Daten der Verteilung nicht folgen (H0 nicht zurückweisen)
- Wenn der p-Wert größer als das Signifikanzniveau ist, weisen Sie die Nullhypothese nicht zurück. Es liegen nicht genügend Anzeichen dafür vor, dass die Daten der Verteilung nicht folgen. Sie können annehmen, dass die Daten der Verteilung folgen.
- Wählen Sie die Verteilung aus, die in Ihrer Branche oder Anwendung am gängigsten ist.
- Wählen Sie die Verteilung aus, die die konservativsten Ergebnisse liefert. Sie können beispielsweise eine Prozessfähigkeitsanalyse mit verschiedenen Verteilungen durchführen und anschließend die Verteilung auswählen, die die konservativsten Prozessfähigkeitsindizes liefert. Weitere Informationen finden Sie unter Verteilungsperzentile für Identifikation der Verteilung; klicken Sie dort auf „Prozente und Perzentile“.
- Wählen Sie die einfachste Verteilung aus, die eine gute Anpassung an die Daten bietet. Wenn beispielsweise sowohl eine Verteilung mit 2 Parametern als auch eine Verteilung mit 3 Parametern eine gute Anpassung bieten, könnten Sie die einfachere Verteilung mit 2 Parametern auswählen.
Wichtig
Seien Sie beim Interpretieren von Ergebnissen, die aus sehr kleinen oder sehr großen Stichproben stammen, vorsichtig. Bei einer sehr kleinen Stichprobe besitzt ein Test der Anpassungsgüte möglicherweise nicht die erforderliche Trennschärfe, um signifikante Abweichungen von der Verteilung zu erkennen. Bei einer sehr großen Stichprobe hingegen ist die Trennschärfe so groß, dass auch kleine Abweichungen von der Verteilung erkannt werden, die keine praktische Bedeutung besitzen. Verwenden Sie zusätzlich zu den p-Werten die Wahrscheinlichkeitsnetze, um die Verteilungsanpassung zu beurteilen.
Test auf Güte der Anpassung
| Verteilung | AD | p | LVT p |
|---|---|---|---|
| Normal | 0,754 | 0,046 | |
| Box-Cox-Transformation | 0,414 | 0,324 | |
| Lognormal | 0,650 | 0,085 | |
| Lognormal mit 3 Parametern | 0,341 | * | 0,017 |
| Exponential | 20,614 | <0,003 | |
| Exponential mit 2 Parametern | 1,684 | 0,014 | 0,000 |
| Weibull | 1,442 | <0,010 | |
| Weibull mit 3 Parametern | 0,230 | >0,500 | 0,000 |
| Kleinster Extremwert | 1,656 | <0,010 | |
| Größter Extremwert | 0,394 | >0,250 | |
| Gamma | 0,702 | 0,071 | |
| Gamma mit 3 Parametern | 0,268 | * | 0,006 |
| Logistisch | 0,726 | 0,034 | |
| Loglogistisch | 0,659 | 0,050 | |
| Loglogistisch mit 3 Parametern | 0,432 | * | 0,027 |
| Johnson-Transformation | 0,124 | 0,986 |
Wichtigste Ergebnisse: p
In diesen Ergebnissen weisen mehrere Verteilungen einen p-Wert auf, der größer als 0,05 ist. Die Weibull-Verteilung mit 3 Parametern (p > 0,500) und die Verteilung des größten Extremwerts (p > 0,250) haben die größten p-Werte und scheinen eine bessere Anpassung an die Stichprobendaten als die anderen Verteilungen zu bieten. Außerdem können die Daten gut mit der Box-Cox-Transformation (p = 0,353) und der Johnson-Transformation (p = 0,986) transformiert werden, so dass diese einer Normalverteilung folgen.
Hinweis
Bei einer Reihe von Verteilungen zeigt Minitab außerdem die Ergebnisse für die betreffende Verteilung mit einem zusätzlichen Parameter an. Zum Beispiel zeigt Minitab für die lognormale Verteilung die Ergebnisse für die Verteilung mit 2 Parametern und mit 3 Parametern an. Verwenden Sie bei Verteilungen mit zusätzlichen Parametern den p-Wert des Likelihood-Verhältnis-Tests (LVT p), um zu ermitteln, ob die Anpassung der Verteilung signifikant verbessert wird, wenn ein zusätzlicher Parameter hinzugefügt wird. Ein LVT-p-Wert kleiner als 0,05 deutet auf eine signifikante Verbesserung der Anpassung hin. Weitere Informationen finden Sie unter Güte der Anpassung für Identifikation der Verteilung; klicken Sie dort auf „LVT p“.
