In diesem Thema
Box-Cox-Transformation (λ)
Wenn Sie bei der Identifikation der Verteilung die Box-Cox-Transformation anfordern, gibt Minitab den in der Transformation verwendeten Wert von Lambda (λ) aus.
Mit der Box-Cox-Transformation wird ein Lambda-Wert geschätzt (wie unten veranschaulicht), der die Standardabweichung einer standardisierten transformierten Variablen minimiert. Die resultierende Transformation ist Yλ, wenn λ ҂ 0; sie ist In Y, wenn λ = 0.
Bei dieser Methode werden viele Arten von Transformationen durchsucht. In der folgenden Tabelle sind einige der gängigsten Transformationen aufgeführt, wobei Y' die Transformation des Y der Daten darstellt:
| Lambda-Wert (λ) | Transformation |
|---|---|
 |
 |
 |
 |
 |
 |
 |
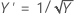 |
 |
 |
Johnson-Transformationsfunktion
Wenn Sie bei der Identifikation der Verteilung die Johnson-Transformationsfunktion anfordern, gibt Minitab die zum Transformieren der Daten verwendete Funktion aus. Angenommen, die Johnson-Transformationsfunktion lautet 0,762475 + 0,870902 × Ln((x – 46,3174)/(59,6770 – x)). Wenn der ursprüngliche Datenwert für x gleich 50 ist, wird der transformierte Datenwert für 50 wie folgt berechnet: 0,762475 + 0,870902 × Ln((50 – 46,3174)/(59,6770 – 50)), was –0,07893 ergibt.
Weitere Informationen zum Algorithmus, mit dem Minitab die Johnson-Transformationsfunktion ermittelt, finden Sie unter Methoden und Formeln für Transformationen in Identifikation der Verteilung.
