Maximum-Likelihood-Schätzungen von Verteilungsparametern
Mit der Maximum-Likelihood-Methode werden die Werte der Verteilungsparameter geschätzt, die die Likelihood-Funktion für jede Verteilung maximieren. Ziel ist es, die beste „Übereinstimmung“ zwischen dem Verteilungsmodell und den beobachteten Stichprobendaten zu erhalten.
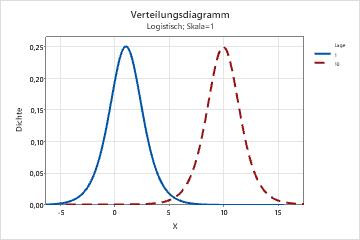
- Lage
- Dieser Parameter wirkt sich auf die Lage einer Verteilung aus. Mit
verschiedenen Lageparametern wird zum Beispiel eine logistische Verteilung
entlang der horizontalen Achse verschoben.
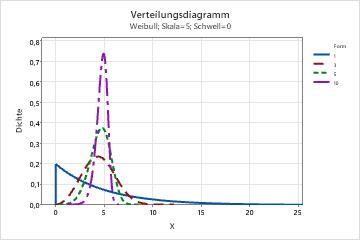
- Form
- Dieser Parameter wirkt sich auf die Form der Verteilung aus. Mit
verschiedenen Formparametern erscheint zum Beispiel eine Weibull-Verteilung
schiefer oder symmetrischer.
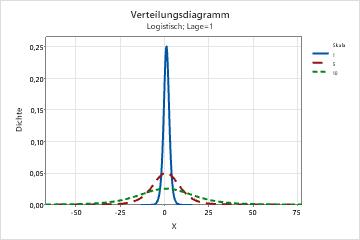
- Skala
- Dieser Parameter wirkt sich auf die Skala der Verteilung aus. Mit
verschiedenen Skalenparametern erscheint zum Beispiel eine logistische
Verteilung „gedehnter“ oder komprimierter.
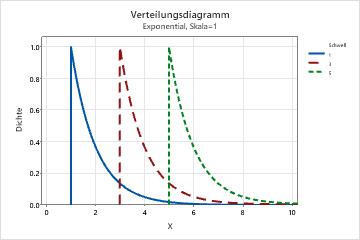
- Schwellenwert
- Dieser Parameter wirkt sich auf das Minimum einer Zufallsvariable aus. Mit
verschiedenen Schwellenwertparametern wird zum Beispiel eine
Exponentialverteilung für einen anderen Wertebereich definiert.
Hinweis
Minitab verwendet die Maximum-Likelihood-Methode zum Berechnen der Parameterschätzwerte für alle Verteilungen mit Ausnahme der Normalverteilung und der lognormalen Verteilung, für die stattdessen erwartungstreue Parameterschätzwerte verwendet werden.
Interpretation
Verwenden Sie die Maximum-Likelihood-Schätzwerte der Verteilungsparameter, um das für Ihre Daten verwendete spezifische Verteilungsmodell besser zu verstehen. Angenommen, ein Qualitätstechniker bestimmt auf der Grundlage des historischen Prozesswissens sowie der Anderson-Darling- und LVT-p-Werte, dass die Weibull-Verteilung mit 3 Parametern die beste Anpassung für die Prozessdaten bietet. Um die spezifische Weibull-Verteilung mit 3 Parametern zu verstehen, die zum Modellieren der Daten verwendet wird, untersucht der Techniker die Maximum-Likelihood-Schätzwerte für Form, Skala und Schwellenwert, die für die Verteilung berechnet wurden.
Verteilung
Die Identifikation der Verteilung liefert Statistiken für die Güte der Anpassung und Verteilungsparameter für eine Reihe von häufig verwendeten Verteilungen. Viele dieser Verteilungen sind vielseitig und können eine Reihe von stetigen Daten modellieren, darunter Daten mit positiven Werten, negativen Werten und 0.
- Lognormal mit 2 Parametern
- Exponential mit 1 Parametern
- Weibull mit 2 Parametern
- Gamma mit 2 Parametern
- Loglogistisch mit 2 Parametern
Wenn Ihre Daten daher negative Werte oder 0 enthalten, gibt Minitab für diese speziellen Verteilungen keine Ergebnisse aus. Verwenden Sie in diesem Fall die Ergebnisse für die jeweilige Version der Verteilung mit mehr Parametern. Wenn die Daten zum Beispiel negative Werte enthalten, liefert Minitab keine Ergebnisse für die lognormale Verteilung mit 2 Parametern. Verwenden Sie stattdessen die Ergebnisse für die lognormale Verteilung mit 3 Parametern.
Weitere Informationen zu den in der Identifikation der Verteilung verwendeten Verteilungen finden Sie unter Weshalb ist Weibull-Verteilung die Standardverteilung für die Prozessfähigkeitsanalyse für nicht normalverteilte Daten?.
Hinweis
Informationen zu den Formeln, mit denen PDF und CDF für die einzelnen Verteilungen berechnet werden, finden Sie unter Methoden und Formeln für Verteilungen in Identifikation der Verteilung.
