N
Die Anzahl der nicht fehlenden Werte in der Stichprobe. N ist die Anzahl aller beobachteten Werte.
| Gesamt | N | N* |
|---|---|---|
| 149 | 141 | 8 |
Interpretation
Verwenden Sie N, um den Umfang der Stichprobe festzustellen.
Wichtig
Seien Sie beim Interpretieren von Ergebnissen, die aus sehr kleinen oder sehr großen Stichproben stammen, vorsichtig. Bei einer sehr kleinen Stichprobe besitzt ein Test der Anpassungsgüte möglicherweise nicht die erforderliche Trennschärfe, um signifikante Abweichungen von der Verteilung zu erkennen. Bei einer sehr großen Stichprobe hingegen ist die Trennschärfe so groß, dass auch kleine Abweichungen von der Verteilung erkannt werden, die keine praktische Bedeutung besitzen. Verwenden Sie zusätzlich zu den p-Werten die Wahrscheinlichkeitsnetze, um die Verteilungsanpassung zu beurteilen.
N*
Die Anzahl der fehlenden Werte in der Stichprobe. N* ist die Anzahl der Zellen im Arbeitsblatt, die das Symbol für fehlende Werte „*“ enthalten.
| Gesamt | N | N* |
|---|---|---|
| 149 | 141 | 8 |
Mittelwert
Der Mittelwert wird als Durchschnitt der Daten berechnet; hierbei handelt es sich um die Summe aller Beobachtungen dividiert durch die Anzahl der Beobachtungen.
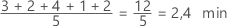
Interpretation
Verwenden Sie den Mittelwert, um die Stichprobe mit einem einzelnen Wert zu beschreiben, der das Zentrum der Daten darstellt. In vielen statistischen Analysen wird der Mittelwert als Standardreferenzpunkt verwendet.
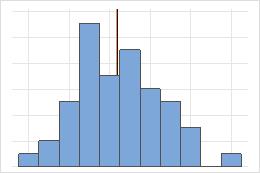
Mittelwert und Median in einer symmetrischen Verteilung
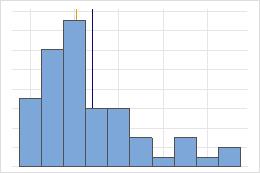
Mittelwert und Median in einer nicht symmetrischen Verteilung
Bei der symmetrischen Verteilung sind der Mittelwert (blaue Linie) und der Median (orangefarbene Linie) nahezu identisch. Daher überlappen sich die Linien und können nicht voneinander unterschieden werden. Bei der nicht symmetrischen Verteilung sind die Daten rechtsschief. Dies führt dazu, dass der Mittelwert größer als der Median ist.
StdAbw
Die Standardabweichung (StdAbw) ist das am häufigsten verwendete Maß für die Streuung bzw. die Streubreite der Daten um den Mittelwert. Die Standardabweichung einer Grundgesamtheit wird häufig mit dem Symbol σ (Sigma) angegeben, und die Standardabweichung einer Stichprobe wird mit s dargestellt.
Interpretation
Bestimmen Sie anhand der Standardabweichung die Streubreite der Daten um den Mittelwert. Eine größere Stichproben-Standardabweichung verweist darauf, dass die Daten breiter um den Mittelwert gestreut sind.

Krankenhaus 1
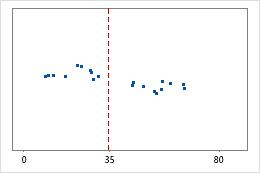
Krankenhaus 2
Zeit bis zur Entlassung in Krankenhäusern
Verwaltungsangestellte zeichnen die Zeit bis zur Entlassung von Patienten auf, die in der Notaufnahme zweier Krankenhäuser behandelt werden. Obwohl die durchschnittliche Zeit bis zur Entlassung in etwa identisch ist (35 Minuten), weichen die Standardabweichungen signifikant voneinander ab. Die Standardabweichung für Krankenhaus 1 beträgt etwa 6. Im Durchschnitt weicht die Zeit bis zur Entlassung eines Patienten um etwa 6 Minuten vom Mittelwert (gestrichelte Linie) ab. Die Standardabweichung für Krankenhaus 2 beträgt etwa 20. Im Durchschnitt weicht die Zeit bis zur Entlassung eines Patienten um ca. 20 Minuten vom Mittelwert (gestrichelte Linie) ab.
Median
Der Median ist der Mittelpunkt des Datensatzes. Dieser Wert gibt den Punkt an, an dem die Hälfte der Beobachtungen über dem Wert und die Hälfte der Beobachtungen unter dem Wert liegen. Der Median wird durch Bilden einer Rangfolge der Beobachtungen und Ermitteln der Beobachtung an der Stelle [N + 1] / 2 in der Rangfolge bestimmt. Bei einer geraden Anzahl an Beobachtungen ist der Median der Wert zwischen den Beobachtungen an den Stellen N / 2 und [N / 2] + 1.

Für diese geordneten Daten ist der Median 13. Das heißt, die Hälfte der Werte ist kleiner oder gleich 13, und die andere Hälfte der Werte ist größer oder gleich 13.
Interpretation

Mittelwert und Median in einer symmetrischen Verteilung

Mittelwert und Median in einer nicht symmetrischen Verteilung
Bei der symmetrischen Verteilung sind der Mittelwert (blaue Linie) und der Median (orangefarbene Linie) nahezu identisch. Daher überlappen sich die Linien und können nicht voneinander unterschieden werden. Bei der nicht symmetrischen Verteilung sind die Daten rechtsschief. Dies führt dazu, dass der Mittelwert größer als der Median ist.
Minimum
Der kleinste Datenwert.
In diesen Daten ist das Minimum 7.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interpretation
Verwenden Sie das Minimum, um einen möglichen Ausreißer zu identifizieren. Wenn der Wert ungewöhnlich klein ist, untersuchen Sie die möglichen Ursachen, z. B. ob es sich um einen Dateneingabe- oder Messfehler handelt.
Eine der einfachsten Möglichkeiten, um die Streuung in den Daten zu untersuchen, ist ein Vergleich von Minimum und Maximum, um die Spannweite zu ermitteln. Die Spannweite ist die Differenz zwischen dem Maximum und dem Minimum im Datensatz. Bei der Auswertung der Streuung in den Daten sollten Sie auch andere Maße berücksichtigen, z. B. die Standardabweichung.
Maximum
Der größte Datenwert.
In diesen Daten ist das Maximum 19.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interpretation
Verwenden Sie das Maximum, um einen möglichen Ausreißer zu identifizieren. Wenn der Wert ungewöhnlich groß ist, untersuchen Sie die möglichen Ursachen, z. B. ob es sich um einen Dateneingabe- oder Messfehler handelt.
Eine der einfachsten Möglichkeiten, um die Streuung in den Daten zu untersuchen, ist ein Vergleich von Minimum und Maximum, um die Spannweite zu ermitteln. Die Spannweite ist die Differenz zwischen dem Maximum und dem Minimum im Datensatz. Bei der Auswertung der Streuung in den Daten sollten Sie auch andere Maße berücksichtigen, z. B. die Standardabweichung.
Schiefe
Die Schiefe gibt das Ausmaß an, in dem die Daten asymmetrisch sind.
Interpretation
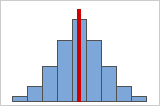
Abbildung A: Symmetrische, normalverteilte Daten
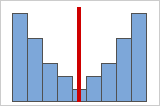
Abbildung B: Symmetrische, nicht normalverteilte Daten
Symmetrische oder nicht schiefe Verteilungen
Bei zunehmender Symmetrie der Daten nähert sich ihr Schiefewert 0 an. Abbildung A zeigt normalverteilte Daten, die per definitionem eine relativ geringe Schiefe aufweisen. Die Linie in der Mitte des Histogramms von normalverteilten Daten zeigt, dass die beiden Seiten einander spiegeln. Eine fehlende Schiefe allein impliziert jedoch keine Normalverteilung. Abbildung B zeigt eine Verteilung, bei der beide Seiten einander spiegeln, die Daten jedoch nicht normalverteilt sind.
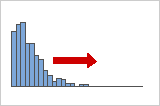
Positiv schiefe oder rechtsschiefe Verteilungen
Positiv schiefe Daten werden auch als rechtsschief verteilte Daten bezeichnet, weil der Randbereich der Verteilung nach rechts zeigt. Der Schiefewert von positiv schiefen Daten ist größer als 0. Gehaltsdaten sind oft positiv schief: Viele Mitarbeiter eines Unternehmens erhalten ein relativ kleines Gehalt, während immer weniger Personen sehr hohe Gehälter beziehen.
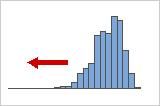
Negativ schiefe oder linksschiefe Verteilungen
Negativ schiefe Daten werden oft als linksschiefe Daten bezeichnet, weil der Randbereich der Verteilung nach links weist. Der Schiefewert von negativ schiefen Daten ist kleiner als 0. Ausfallratendaten sind häufig negativ schief. Zum Beispiel brennen sehr wenige Glühlampen sofort durch, wohingegen die meisten Lampen lange Zeit nicht durchbrennen.
Kurtosis
Die Kurtosis gibt an, wie weit die Randbereiche einer Verteilung von der Normalverteilung abweichen.
Interpretation
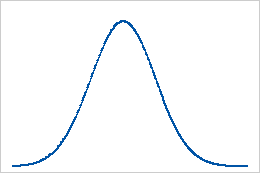
Basislinie: Kurtosis-Wert 0
Daten, die perfekt einer Normalverteilung folgen, weisen den Kurtosis-Wert 0 auf. Normalverteilte Daten bilden die Basislinie für die Kurtosis. Wenn die Kurtosis wesentlich von 0 abweicht, kann dies darauf hinweisen, dass die Daten nicht normalverteilt sind.

Positive Kurtosis
Ein positiver Kurtosis-Wert für eine Verteilung deutet darauf hin, dass sich die Verteilung durch stärker ausgeprägte Randbereiche als die Normalverteilung auszeichnet. Daten, die einer t-Verteilung folgen, weisen beispielsweise einen positiven Kurtosis-Wert auf. Die durchgezogene Linie stellt die Normalverteilung und die gepunktete Linie eine t-Verteilung mit einem positiven Kurtosis-Wert dar.
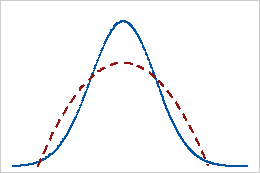
Negative Kurtosis
Ein negativer Kurtosis-Wert für eine Verteilung deutet darauf hin, dass sich die Verteilung durch schwächer ausgeprägte Randbereiche als die Normalverteilung auszeichnet. Daten, die einer Betaverteilung folgen, deren erster und zweiter Formparameter gleich 2 ist, weisen beispielsweise einen negativen Kurtosis-Wert auf. Die durchgezogene Linie stellt die Normalverteilung und die gepunktete Linie eine Betaverteilung mit einem negativen Kurtosis-Wert dar.
