Beispiel für Identifikation der Verteilung

Ein Qualitätstechniker für einen Hersteller von Nahrungsmittelzusätzen möchten den Kalziumgehalt in Vitaminkapseln auswerten. Er erfasst eine Zufallsstichprobe von Kapseln und zeichnet deren Kalziumgehalt auf. Um die geeignete statistische Analyse für die Daten zu ermitteln, muss der Techniker zunächst die Verteilung der Daten bestimmen.

Der Techniker führt eine Identifikation der Verteilung durch, um zu ermitteln, welche Verteilung am besten an die Daten angepasst ist.

Öffnen Sie die Beispieldaten Kalziumgehalt.MTW.
Wählen Sie Statistik > Qualitätswerkzeuge > Identifikation der Verteilung aus.
Wählen Sie im Feld Anordnung der Daten die Option Einzelne Spalte aus, und geben Sie dann Kalzium ein.
Geben Sie im Feld Teilgruppengröße den Wert 1 ein.
Klicken Sie auf OK.

Interpretieren der Ergebnisse

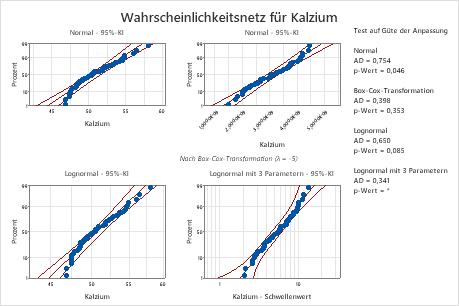
Minitab zeigt für jede Verteilung und Transformation ein Wahrscheinlichkeitsnetz und einen p-Wert an. Wenn eine Verteilung eine gute Anpassung an die Daten bietet (oder wenn eine Transformation effektiv ist), folgen die Punkte im Diagramm einer Geraden innerhalb der Konfidenzgrenzen, und der p-Wert ist größer als das Alpha-Niveau. Häufig wird ein Alpha-Niveau von 0,05 verwendet. Der p-Wert für den Likelihood-Quotienten-Test (LVT p) gibt an, ob die Anpassung einer Verteilung signifikant verbessert wird, wenn ihr ein zusätzlicher Parameter hinzugefügt wird. Ein LVT-p-Wert kleiner als 0,05 deutet auf eine signifikante Verbesserung hin.

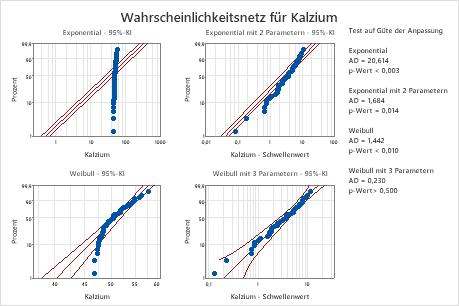
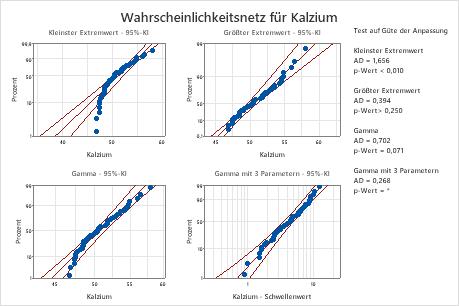
Bei diesen Daten bieten die Weibull-Verteilung mit 3 Parametern (p > 0,500) und die Verteilung des größten Extremwerts (p > 0,250) eine gute Anpassung an die Daten. Durch Hinzufügen eines dritten Parameters wird die Anpassung der lognormalen Verteilung (LVT p = 0,017), der Weibull-Verteilung (LVT p = 0,000), der Gamma-Verteilung (LVT p = 0,006) und der loglogistischen Verteilung (LVT p = 0,027) signifikant verbessert.

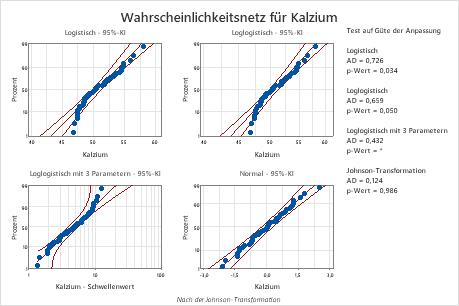
Die Box-Cox-Transformation (p = 0,324) und die Johnson-Transformation (p = 0,986) sind für diese Daten wirksam. Nach der Transformation bietet die Normalverteilung eine gute Anpassung an die transformierten Werte.

Exponential mit 2 Parametern

* WARNUNG * Varianz-/Kovarianzmatrix von geschätzten Parametern ist nicht vorhanden. Der
Schwellenwertparameter wird als fest angenommen, wenn Konfidenzintervalle berechnet werden.

Gamma mit 3 Parametern

* WARNUNG * Varianz-/Kovarianzmatrix von geschätzten Parametern ist nicht vorhanden. Der
Schwellenwertparameter wird als fest angenommen, wenn Konfidenzintervalle berechnet werden.

Verteilung	AD	p	LVT p
Normal	0,754	0,046
Box-Cox-Transformation	0,414	0,324
Lognormal	0,650	0,085
Lognormal mit 3 Parametern	0,341	*	0,017
Exponential	20,614	<0,003
Exponential mit 2 Parametern	1,684	0,014	0,000
Weibull	1,442	<0,010
Weibull mit 3 Parametern	0,230	>0,500	0,000
Kleinster Extremwert	1,656	<0,010
Größter Extremwert	0,394	>0,250
Gamma	0,702	0,071
Gamma mit 3 Parametern	0,268	*	0,006
Logistisch	0,726	0,034
Loglogistisch	0,659	0,050
Loglogistisch mit 3 Parametern	0,432	*	0,027
Johnson-Transformation	0,124	0,986

Verteilung	Lage	Form	Skala	Schwellenwert
Normal*	50,78200		2,76477
Box-Cox-Transformation*	0,00000		0,00000
Lognormal*	3,92612		0,05368
Lognormal mit 3 Parametern	1,69295		0,46849	44,74011
Exponential			50,78200
Exponential mit 2 Parametern			4,06326	46,71873
Weibull		17,82470	52,13681
Weibull mit 3 Parametern		1,47605	4,53647	46,66579
Kleinster Extremwert	52,22257		2,95894
Größter Extremwert	49,50370		2,16992
Gamma		351,04421	0,14466
Gamma mit 3 Parametern		2,99218	1,63698	45,88376
Logistisch	50,57182		1,59483
Loglogistisch	3,92259		0,03121
Loglogistisch mit 3 Parametern	1,54860		0,32763	45,46180
Johnson-Transformation*	0,02897		0,97293

Beispiel für Identifikation der Verteilung

Interpretieren der Ergebnisse

Exponential mit 2 Parametern

Gamma mit 3 Parametern

Deskriptive Statistik

Test auf Güte der Anpassung

ML-Schätzwerte der Verteilungsparameter