Methoden und Formeln für die Linearität des Messgeräts

Wählen Sie die gewünschte Methode oder Formel aus.

In diesem Thema

Linearität
%Linearität
p-Wert für Linearität des Messgeräts
R-Qd
S
Steigung, Konstante

Linearität

Mit der Linearität wird der Unterschied der durchschnittlichen systematischen Messabweichungen über den erwarteten Betriebsbereich des Messsystems bewertet. Die Linearität gibt an, ob das Messgerät für alle Größen gemessener Prüfobjekte die gleiche Genauigkeit aufweist.

Formel

Linearität = | Steigung | * Prozessstreuung

%Linearität

„%Linearität“ ist die als Prozentsatz der Gesamtprozessstreuung ausgedrückte Linearität.

Formel

%Linearität = (Linearität / Prozessstreuung) * 100

p-Wert für Linearität des Messgeräts

Testen Sie mit den p-Werten für die Konstante und Steigung, ob die Steigung gleich 0 und die Konstante gleich 0 ist.

Der p-Wert ist als die Fläche unter der Stichprobenverteilung rechts von + |Teststatistik| und die Fläche unter der Stichprobenverteilung links von - |Teststatistik| definiert. Minitab verwendet die t-Verteilung mit γ df und der t-Statistik, um den p-Wert zu berechnen.

Wenn der p-Wert größer als der α-Wert ist, weisen Sie die Nullhypothese nicht zurück. Es gilt Folgendes:

Wenn der p-Wert für die Konstante größer als der α-Wert ist, weisen Sie die Nullhypothese nicht zurück und schlussfolgern, dass die systematische Messabweichung für alle Referenzwerte gleich 0 ist.
Wenn der p-Wert für die Steigung größer als der α-Wert ist, weisen Sie die Nullhypothese nicht zurück und schlussfolgern, dass das Messsystem für alle Referenzwerte die gleiche systematische Messabweichung aufweist (es ist keine Linearität vorhanden).

Wenn der p-Wert kleiner als der α-Wert ist, weisen Sie die Nullhypothese zurück. Es gilt Folgendes:

Wenn der p-Wert für die Konstante kleiner als der α-Wert ist, weisen Sie die Nullhypothese zurück und schlussfolgern, dass die systematische Messabweichung für alle Referenzwerte ungleich 0 ist.
Wenn der p-Wert für die Steigung kleiner als der α-Wert ist, weisen Sie die Nullhypothese zurück und schlussfolgern, dass das Messsystem nicht die gleiche systematische Messabweichung für alle Referenzwerte aufweist (Linearität ist vorhanden).

R-Qd

R-Qd (R²) ist der Determinationskoeffizient, mit dem überprüft wird, ob eine Anpassungslinie die Daten zutreffend wiedergibt. R-Qd (R²) stellt den Anteil der Streuung in der systematischen Messabweichung dar, der durch die lineare Beziehung zwischen den systematischen Messabweichungen und den Referenzwerten erklärt wird.

Formel

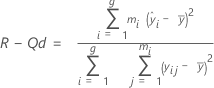
Notation

Begriff	Beschreibung
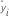	i-ter angepasster Wert der Antwortvariablen
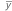	mittlere systematische Messabweichung
y_ij	systematische Messabweichung des j-ten Messwerts des i-ten Teils
g	Anzahl der Teile
m_i	Anzahl der Replikationen des i-ten Teils

S

S ist ein Schätzwert von σ, der Standardabweichung um die Regressionslinie.

Formel

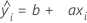
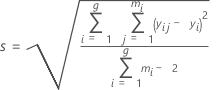
Notation

Begriff	Beschreibung
x_i	Referenzwert für Teil i
y_ij	systematische Messabweichung des j-ten Messwerts des i-ten Teils
g	Anzahl der Teile
m_i	Anzahl der Replikationen des i-ten Teils

Steigung, Konstante

Die Regressionslinie im Diagramm der systematischen Messabweichung im Vergleich zum Referenzwert nimmt die folgende Form an:

Formeln

Steigung der Regressionslinie (a):

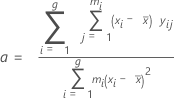
Schnittpunkt der Regressionslinie mit der y-Achse (b):

Notation

Begriff	Beschreibung
a	Steigung
b	Schnittpunkt mit y-Achse
x_i	Referenzwert für Teil i
	durchschnittlicher Referenzwert für alle Teile
y_ij	systematische Messabweichung des j-ten Messwerts des i-ten Teils
g	Anzahl der Teile
m_i	Anzahl der Replikationen des i-ten Teils
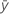	durchschnittliche systematische Messabweichung insgesamt