In diesem Thema
Diagramm „Systematische Messabweichung vs. Referenzwert“,
Ermitteln Sie anhand des Diagramms „Systematische Messabweichung vs. Referenzwert“, wie die Werte der systematischen Messabweichung für die einzelnen Teile variieren. Die blauen Punkte stellen die Werte der systematischen Messabweichung für die einzelnen Referenzwerte dar. Das rote Quadrat stellt den Durchschnittswert der systematischen Messabweichung für die einzelnen Referenzwerte dar. Die Linie ist die mit einer Regression nach der Methode der kleinsten Quadrate an die durchschnittlichen Abweichungen angepasste Linie.
Interpretation
Im Idealfall liegen die Abweichungen für jedes Teil nahe 0, und die Anpassungslinie ist horizontal.
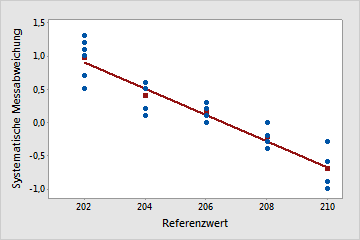
Linearität scheint ein Problem darzustellen.
Die dargestellte Linie weist eine Steigung auf. In diesem Beispiel sind die Messwerte für kleinere Teile größer als die Werte für die entsprechenden Referenzteile. Die Messwerte für größere Teile sind tendenziell kleiner als die Werte für die entsprechenden Referenzteile.
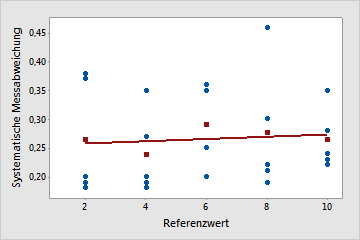
Linearität scheint kein Problem darzustellen.
Die dargestellte Linie ist nahezu horizontal; dies verweist darauf, dass die durchschnittliche systematische Messabweichung relativ konstant ist und nicht vom Referenzwert abhängt. In diesem Beispiel liegen die Messwerte für alle Teile höher als die Messwerte für die entsprechenden Referenzteile.
Koef
Die Koeffizienten sind die Zahlen aus der Gleichung für die Regressionslinie im Diagramm der systematischen Messabweichung im Vergleich mit dem Referenzwert.
Die Gleichung für die Linie der Regression kleinster Quadrate weist die folgende allgemeine Form auf:
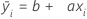
Der Term b stellt den konstanten Koeffizienten dar. Er gibt den Schnittpunkt der Anpassungslinie mit der y-Achse an.
Der Term a stellt den Steigungskoeffizienten dar. Die Steigung einer Linie gibt deren Steilheit an; hierbei handelt es sich um die Änderung auf der y-Achse gegenüber der Änderung auf der x-Achse.
Interpretation
Bei einem sehr kleinen Steigungskoeffizienten ist die Steigung nahezu horizontal. Damit ist die systematische Messabweichung für alle Referenzwerte relativ konstant, und die Linearität stellt kein signifikantes Problem dar. Größere absolute Werte des Steigungskoeffizienten |a| geben eine steilere Steigung der Linie an. Ist der p-Wert der Steigung kleiner als Alpha, so ist die Linearität signifikant.
Wenn keine signifikante Linearität vorliegt, geben größere absolute Werte des konstanten Koeffizienten |b| eine größere systematische Messabweichung an. Wenn eine signifikante Linearität vorhanden ist, müssen Sie die einzelnen Werte für die systematische Messabweichung untersuchen.
SE Koef
Der Standardfehler des Schätzwerts eines Regressionskoeffizienten misst, wie präzise das Modell den unbekannten Wert des Koeffizienten schätzt. Der Standardfehler des Koeffizienten ist immer positiv.
Interpretation
Verwenden Sie den Standardfehler des Koeffizienten, um die Präzision des Schätzwerts für den Koeffizienten zu ermitteln. Je geringer der Standardfehler ist, desto präziser ist der Schätzwert. Durch Dividieren des Koeffizienten durch seinen Standardfehler wird ein t-Wert berechnet. Wenn der zum t-Wert gehörende p-Wert kleiner als das α-Niveau ist, können Sie schlussfolgern, dass sich der Koeffizient signifikant von 0 unterscheidet.
p-Wert für Linearität des Messgeräts
- p-Wert für Konstante: Testen Sie hiermit, ob die Konstante der Linearitätslinie gleich 0 ist.
- p-Wert für Steigung: Testen Sie hiermit, ob die Steigung der Linearitätslinie gleich 0 ist.
Interpretation
- Wenn der p-Wert für die Konstante größer als der α-Wert ist, weisen Sie die Nullhypothese nicht zurück und schlussfolgern, dass die systematische Messabweichung für alle Referenzwerte gleich 0 ist.
- Wenn der p-Wert für die Steigung größer als der α-Wert ist, weisen Sie die Nullhypothese nicht zurück und schlussfolgern, dass das Messsystem für alle Referenzwerte die gleiche systematische Messabweichung aufweist (es ist keine Linearität vorhanden).
- Wenn der p-Wert für die Konstante kleiner als der α-Wert ist, weisen Sie die Nullhypothese zurück und schlussfolgern, dass die systematische Messabweichung für alle Referenzwerte ungleich 0 ist.
- Wenn der p-Wert für die Steigung kleiner als der α-Wert ist, weisen Sie die Nullhypothese zurück und schlussfolgern, dass das Messsystem nicht die gleiche systematische Messabweichung für alle Referenzwerte aufweist (Linearität ist vorhanden).
S und R-Qd
S und R-Qd (R2) sind Maßzahlen dafür, wie gut das Modell an die Daten angepasst ist.
S ist ein Schätzwert von σ, der Standardabweichung um die Regressionslinie.
R-Qd (R2) stellt den Anteil der Streuung in der systematischen Messabweichung dar, der durch die lineare Beziehung zwischen den systematischen Messabweichungen und den Referenzwerten erklärt wird.
Interpretation
Kleinere Werte von S verweisen auf eine geringere Streuung in den Schätzwerten für die systematische Messabweichung. R2 kann im Bereich von 0 bis 100 % liegen. Im Allgemeinen gilt: Je höher der R2-Wert, desto besser ist das Modell an die Daten angepasst.
Linearität, %Linearität
Mit der Linearität wird der Unterschied der durchschnittlichen systematischen Messabweichungen über den erwarteten Betriebsbereich des Messsystems bewertet. Die Linearität gibt an, ob das Messgerät für alle Referenzwerte die gleiche Genauigkeit (die gleiche systematische Messabweichung) aufweist.
„%Linearität“ ist die als Prozentsatz der Prozessstreuung ausgedrückte Linearität.
Interpretation
Um die Linearität Ihrer Daten zu interpretieren, ermitteln Sie, ob sich die systematische Messabweichung über die Referenzwerte hinweg ändert. Wenn die Daten in einem Streudiagramm keine horizontale Linie ergeben, liegt Linearität vor. Im Idealfall ist die Anpassungslinie horizontal, und sie liegt nah bei 0.

Linearität scheint ein Problem darzustellen.
Die dargestellte Linie weist eine Steigung auf. In diesem Beispiel sind die Messwerte für kleinere Teile größer als die Werte für die entsprechenden Referenzteile. Die Messwerte für größere Teile sind tendenziell kleiner als die Werte für die entsprechenden Referenzteile.

Linearität scheint kein Problem darzustellen.
Die dargestellte Linie ist nahezu horizontal; dies verweist darauf, dass die durchschnittliche systematische Messabweichung relativ konstant ist und nicht vom Referenzwert abhängt. In diesem Beispiel liegen die Messwerte für alle Teile höher als die Messwerte für die entsprechenden Referenzteile.
Bei einem Messgerät, das für alle Teile beständige Messwerte liefert, liegt „%Linearität“ nahe 0.
Systematische Messabweichung, %systematische Messabweichung
Die systematische Messabweichung wird als Differenz zwischen dem bekannten Standardwert eines Referenzteils und dem beobachteten Durchschnittsmesswert berechnet.Die systematische Messabweichung ist ein Maß für die Genauigkeit eines Messsystems.
%systematische Messabweichung ist die systematische Messabweichung ausgedrückt als Prozentsatz der Prozessstreuung.
Interpretation
- Eine positive systematische Messabweichung bedeutet, dass das Messgerät zu hohe Messwerte liefert.
- Eine negative systematische Messabweichung bedeutet, dass das Messgerät zu niedrige Messwerte liefert.
Bei einem Messgerät, das präzise misst, ist %systematische Messabweichung gering.
p-Wert für systematische Abweichung des Messgeräts
- p-Wert für durchschnittliche systematische Messabweichung: Testen Sie hiermit, ob die durchschnittliche systematische Messabweichung gleich 0 ist.
- p-Wert für jeden Referenzwert: Testen Sie hiermit, ob die systematische Messabweichung bei jedem Referenzwert gleich 0 ist.
Interpretation
- Wenn der p-Wert für jeden Referenzwert größer als der α-Wert ist, weisen Sie die Nullhypothese nicht zurück und folgern, dass die systematische Messabweichung gleich 0 ist.
- Wenn der p-Wert für die durchschnittliche systematische Messabweichung größer als der α-Wert ist, weisen Sie die Nullhypothese zurück und folgern, dass die durchschnittliche systematische Messabweichung gleich 0 ist.
- Wenn der p-Wert für jeden Referenzwert kleiner als der α-Wert ist, weisen Sie die Nullhypothese zurück und folgern, dass die systematische Messabweichung ungleich 0 ist.
- Wenn der p-Wert für die durchschnittliche systematische Messabweichung kleiner als der α-Wert ist, weisen Sie die Nullhypothese zurück und folgern, dass die durchschnittliche systematische Messabweichung ungleich 0 ist.
