In diesem Thema
- %Toleranz (SU/Tol)
- %Prozess (SU/Proz)
- Anzahl der eindeutigen Kategorien
- Wahrscheinlichkeiten der Fehlklassifikation
- VDA 5
- Grafik „Streuungskomponenten“
- X-quer-Karte
- R-Karte
- Diagramm der Messwerte nach einem einzelnen Faktor (Teil) angeordnet
- Diagramm der Messwerte nach einem einzelnen Faktor (Prüfer) angeordnet
- Diagramm der Wechselwirkung (Prüfer*Teil)
DF
Die Freiheitsgrade (DF) für jede SS (Summe der Quadrate). Im Allgemeinen erfasst DF, wie viele Informationen zum Berechnen von der einzelnen Summen der Quadrate verfügbar sind.
Seq SS
Die sequenzielle Summe der Quadrate für die einzelnen Terme im Modell (Faktor oder Wechselwirkung) stellt den Streuungsgrad in der Antwortvariablen dar, der dadurch erklärt wird, dass die einzelnen Terme dem Modell nacheinander hinzugefügt werden, und zwar in der unter Quelle aufgeführten Reihenfolge. Deswegen bezieht sich die sequenzielle Summe der Quadrate bei Termen speziell auf die Reihenfolge der Terme, die im Modell angegeben wurden.
SS Gesamt = SS Teil + SS Prüfer + SS Andere Faktoren + SS Prüfer * Teil + SS Andere Wechselwirkungen + SS Wiederholbarkeit
Kor SS
Die korrigierte Summe der Quadrate ist ein Maß für die Streuung verschiedener Komponenten im Modell. Die Reihenfolge der Terme (Faktoren oder Wechselwirkungen) im Modell wirkt sich nicht auf die Berechnung der korrigierten Summe der Quadrate aus. In der ANOVA-Tabelle verteilt Minitab die Summe der Quadrate auf verschiedene Komponenten, die die auf unterschiedliche Quellen zurückzuführende Streuung beschreiben.
Kor MS
Mit dem korrigierten Mittel der Quadrate wird angegeben, wie viel der Streuung von einem Term oder einem Modell erklärt wird; hierbei wird angenommen, dass alle übrigen Terme im Modell enthalten sind, jedoch außer Acht gelassen, in welcher Reihenfolge diese in das Modell aufgenommen wurden. Im Unterschied zur korrigierten Summe der Quadrate werden beim korrigierten Mittel der Quadrate die Freiheitsgrade berücksichtigt.
Kor MS = Kor SS/DF für jede Streuungsquelle
Minitab verwendet das korrigierte Mittel der Quadrate, um den p-Wert für einen Term zu berechnen.
F
Die Statistik, mit der ermittelt wird, ob die Faktoreffekte wie Prüfer und Teil sowie die Wechselwirkungseffekte wie Prüfer*Teil statistisch signifikant sind.
Je größer die F-Statistik, desto höher ist die Wahrscheinlichkeit, dass der Faktor erheblich zur Streuung in der Antwortvariablen (der Variablen, für die Messwerte erfasst werden) beiträgt.
p
Der p-Wert gibt die Wahrscheinlichkeit an, eine Teststatistik (wie die F-Statistik) zu erhalten, die mindestens so extrem wie der aus der Stichprobe berechnete Wert ist, wenn die Nullhypothese wahr ist.
Interpretation
Bestimmen Sie mit dem p-Wert in der ANOVA-Tabelle, ob sich die durchschnittlichen Messwerte signifikant voneinander unterscheiden. Minitab zeigt die ANOVA-Tabelle nur an, wenn Sie die Option „ANOVA“ für Analysemethode auswählen.
Ein niedriger p-Wert bedeutet, dass die Annahme wahrscheinlich nicht zutrifft, dass alle Teile, Prüfer oder Wechselwirkungen denselben Mittelwert aufweisen.
- p-Wert ≤ α: Mindestens ein Mittelwert weicht statistisch ab
- Wenn der p-Wert kleiner oder gleich dem Signifikanzniveau ist, weisen Sie die Nullhypothese zurück und schlussfolgern, dass sich mindestens einer der Mittelwerte signifikant von den anderen unterscheidet. So erfasst beispielsweise mindestens ein Prüfer abweichende Messwerte.
- p-Wert > α: Die Mittelwerte unterscheiden sich nicht signifikant voneinander
- Wenn der p-Wert größer als das Signifikanzniveau ist, weisen Sie die Nullhypothese nicht zurück, da keine ausreichenden Hinweise für die Schlussfolgerung vorliegen, dass sich die Mittelwerte der Grundgesamtheit voneinander unterscheiden. Sie können beispielsweise nicht schlussfolgern, dass die Prüfer unterschiedlich messen.
VarKomp
VarKomp sind die geschätzten Varianzkomponenten für jede Quelle in einer ANOVA-Tabelle.
Interpretation
Mit den Varianzkomponenten können Sie die Streuung für jede Messfehlerquelle bewerten.
In einem akzeptablen Messsystem ist die größte Streuungskomponente die Streuung zwischen den Teilen. Wenn Wiederholbarkeit und Reproduzierbarkeit eine starke Streuung beitragen, müssen Sie die Ursache des Problems ermitteln und Korrekturmaßnahmen ergreifen.
%Beitrag (der VarKomp)
„%Beitrag“ ist der Prozentsatz der einzelnen Varianzkomponenten an der Gesamtstreuung. Dieser Wert wird berechnet, indem die Varianzkomponente der betreffenden Quelle durch die Gesamtstreuung dividiert und anschließend mit 100 multipliziert wird, um ihn als Prozentsatz auszudrücken.
Interpretation
Mit %Beitrag können Sie die Streuung für jede Messfehlerquelle bewerten.
In einem akzeptablen Messsystem ist die größte Streuungskomponente die Streuung zwischen den Teilen. Wenn Wiederholbarkeit und Reproduzierbarkeit eine starke Streuung beitragen, müssen Sie die Ursache des Problems ermitteln und Korrekturmaßnahmen ergreifen.
StdAbw
„StdAbw“ ist die Standardabweichung für die einzelnen Streuungsquellen. Die Standardabweichung ist die Quadratwurzel der Varianzkomponente für die betreffende Quelle.
Die Standardabweichung ist ein hilfreiches Maß für die Streuung, da sie in der gleichen Einheit wie die Messwerte und die Toleranz des Teils angegeben wird.
Streu. in Unters. (6 * StdAbw)
Die Streuung in der Untersuchung wird berechnet, indem die Standardabweichung für jede Streuungsquelle mit 6 oder einem anderen Multiplikator multipliziert wird, den Sie in Streuung in Untersuchung angeben.
Im Allgemeinen wird die Prozessstreuung als 6s definiert, wobei s die Standardabweichung als Schätzwert der Standardabweichung der Grundgesamtheit (bezeichnet als σ oder Sigma) ist. Wenn die Daten normalverteilt sind, liegen etwa 99,73 % der Daten innerhalb von 6 Standardabweichungen des Mittelwerts. Wenn Sie einen anderen Prozentsatz der Daten festlegen möchten, geben Sie einen anderen Multiplikator für die Standardabweichung an. Wenn Sie beispielsweise die Lage von 99 % der Daten ermitteln möchten, geben Sie anstelle des Standardmultiplikators 6 den Multiplikator 5,15 an.
%Streuung in Untersuchung (%SU)
„%Streuung in Unters.“ wird berechnet, indem die Streuung in der Untersuchung für jede Streuungsquelle durch die Gesamtstreuung dividiert und das Ergebnis mit 100 multipliziert wird.
„%Streuung in Unters.“ ist die Quadratwurzel der berechneten Varianzkomponente (VarKomp) für die betreffende Quelle. Daher summieren sich die Werte für „%Beitrag“ für „VarKomp“ auf 100, während dies bei den Werten für „%Streuung in Unters.“ nicht der Fall ist.
Interpretation
Verwenden Sie den Wert in „%Streuung in Unters.“, um die Streuung des Messsystems mit der Gesamtstreuung zu vergleichen. Wenn Sie das Messsystem zum Beurteilen von Prozessverbesserungen nutzen, beispielsweise zum Reduzieren der Streuung zwischen den Teilen, liefert „%Streuung in Unters.“ einen besseren Schätzwert der Präzision von Messwerten. Wenn Sie die Fähigkeit des Messsystems bewerten möchten, Teile in Bezug auf die Spezifikationen zu messen, ist „%Toleranz“ die geeignete Metrik.
%Toleranz (SU/Tol)
%Toleranz wird berechnet, indem die Streuung in der Untersuchung für jede Quelle durch die Prozesstoleranz dividiert und mit 100 multipliziert wird.
Wenn Sie die Toleranz eingeben, berechnet Minitab %Toleranz, welche die Streuung des Messsystems mit den Spezifikationsgrenzen vergleicht.
Interpretation
Werten Sie mit %Toleranz die Teile in Bezug auf die Spezifikationsgrenze aus. Wenn Sie das Messsystem für die Prozessverbesserung nutzen, beispielsweise zum Reduzieren der Streuung zwischen den Teilen, ist %Streuung in Untersuchung die geeignete Maßzahl.
%Prozess (SU/Proz)
Wenn Sie eine historische Standardabweichung eingeben, die Prozessstreuung jedoch anhand der Teile in der Untersuchung schätzen, berechnet Minitab einen Wert für „%Prozess“. Mit dem Wert von „%Prozess“ wird die Streuung des Messsystems mit der historischen Prozessstreuung verglichen. „%Prozess“ wird berechnet, indem die Streuung in der Untersuchung für jede Quelle durch die historische Prozessstreuung dividiert und mit 100 multipliziert wird. Die Prozessstreuung ist in der Standardeinstellung gleich der historischen Standardabweichung mal 6.
Wenn Sie die Prozessstreuung anhand einer historischen Standardabweichung schätzen, zeigt Minitab „%Prozess“ nicht an, da „%Prozess“ identisch mit „%Streuung in Unters.“ ist.
Anzahl der eindeutigen Kategorien
Die Anzahl der eindeutigen Kategorien ist eine Metrik, mit der in Messsystemanalysen die Fähigkeit eines Messsystems angegeben wird, eine Differenz im gemessenen Merkmal zu erkennen. Die Anzahl der eindeutigen Kategorien stellt die Anzahl der nicht überlappenden Konfidenzintervalle dar, die die Spannweite der Produktstreuung umfassen, welche von den ausgewählten Stichproben definiert wird. Darüber hinaus stellt die Anzahl der eindeutigen Kategorien die Anzahl der Gruppen im Prozess dar, die vom Messsystem unterschieden werden können.
Interpretation
In dem von der Automobile Industry Action Group (AIAG) veröffentlichten Measurement Systems Analysis Manual1 wird empfohlen, dass mindestens fünf Kategorien vorliegen sollten, um auf ein akzeptables Messsystem hinzuweisen. Wenn die Anzahl der eindeutigen Kategorien kleiner als 5 ist, reicht die Auflösung des Messgeräts möglicherweise nicht aus.
Wenn die Anzahl der eindeutigen Kategorien kleiner als 2 ist, ist das Messsystem normalerweise wertlos für die Prozessregelung, da es nicht zwischen Teilen unterscheiden kann. Wenn die Anzahl der Kategorien 2 beträgt, können die Teile lediglich in zwei Gruppen unterteilt werden, z. B. hoch und tief. Beträgt die Anzahl der Kategorien hingegen 3, können die Teile in 3 Gruppen geteilt werden, z. B. hoch, mittel und tief.
Weitere Informationen finden Sie unter Verwenden der Anzahl der eindeutigen Kategorien.
Wahrscheinlichkeiten der Fehlklassifikation
Wenn Sie mindestens eine Spezifikationsgrenze angeben, kann Minitab die Wahrscheinlichkeiten der Fehlklassifikation eines Produkts berechnen. Aufgrund der Streuung des Messsystems ist der gemessene Wert des Teils nicht immer gleich dem tatsächlichen Wert. Der Unterschied zwischen dem gemessenen Wert und dem tatsächlichen Wert bringt die Möglichkeit der Fehlklassifikation des Teils mit sich.
- Verbundene Wahrscheinlichkeit
- Wählen Sie die verbundene Wahrscheinlichkeit aus, wenn noch keine Erkenntnisse über die Annehmbarkeit der Teile vorliegen. Sie nehmen beispielsweise Stichproben von der Fertigungslinie und wissen nicht, ob ein bestimmtes Teil gut oder schlecht ist. Es gibt zwei Fehlklassifikationen, die Sie machen können:
- Die Wahrscheinlichkeit, dass das Teil schlecht ist, Sie es aber annehmen.
- Die Wahrscheinlichkeit, dass das Teil gut ist, Sie es aber ablehnen.
- Bedingte Wahrscheinlichkeit
- Verwenden Sie die bedingte Wahrscheinlichkeit, wenn bereits Erkenntnisse über die Annehmbarkeit der Teile vorliegen. Sie entnehmen zum Beispiel Stichproben von einem Stapel, der nachbearbeitet werden muss, oder von einem Stapel, dessen Produkte für gut befunden wurden und in Kürze ausgeliefert werden sollen. Es gibt zwei Fehlklassifikationen, die Sie machen können:
- Die Wahrscheinlichkeit, dass Sie ein Teil annehmen, das als Stichprobe aus einem Stapel schlechter Produkte gezogen wurde, der nachbearbeitet werden muss (auch als falsche Annahme bezeichnet).
- Die Wahrscheinlichkeit, dass Sie ein Teil zurückweisen, das als Stichprobe aus einem Stapel guter Produkte gezogen wurde, der zur Lieferung ansteht (auch als falsche Rückweisung bezeichnet).
Interpretation
Verbundene Wahrscheinlichkeit
| Beschreibung | Wahrscheinlichkeit |
|---|---|
| Ein zufällig ausgewähltes Teil ist schlecht, wird aber akzeptiert | 0,037 |
| Ein zufällig ausgewähltes Teil ist gut, wird aber zurückgewiesen | 0,055 |
Bedingte Wahrscheinlichkeit
| Beschreibung | Wahrscheinlichkeit |
|---|---|
| Ein Teil aus einer Gruppe von schlechten Produkten wird akzeptiert | 0,151 |
| Ein Teil aus einer Gruppe von guten Produkten wird zurückgewiesen | 0,073 |
Die verbundene Wahrscheinlichkeit, dass ein Teil schlecht ist und Sie es annehmen, beträgt 0,037. Die verbundene Wahrscheinlichkeit, dass ein Teil gut ist und Sie es zurückweisen, beträgt 0,055.
Die bedingte Wahrscheinlichkeit einer falschen Annahme, also dass Sie ein Teil bei der Nachprüfung annehmen, während es tatsächlich nicht den Spezifikationen entspricht, beträgt 0,151. Die bedingte Wahrscheinlichkeit einer falschen Rückweisung, also dass Sie ein Teil bei der Nachprüfung zurückweisen, während es tatsächlich den Spezifikationen entspricht, beträgt 0,073.
VDA 5
Hinweis
VDA 5 ist nur in der Web-App enthalten.
Hinweis
Die Analyse verwendet die maximale Unsicherheit zwischen uEVR, uRE und uEVO, um die Streuung des Messprozesses zu berechnen. Der Prozentsatz der Gesamtsumme für die anderen 2 Statistiken fehlt, da diese Statistiken nicht zur Gesamtsumme beitragen.
- Kalibrierung (uCAL)
- Die Kalibrierung (uCAL) ist die Unsicherheit in den Messungen aus der Kalibrierung des Referenznormals. Diese Statistik ist eine Eingabe für die Analyse. In der Regel stammt dieser Wert aus dem Kalibrierzertifikat.
- Wiederholgenauigkeit am Referenzwert (uEVR)
- Die Wiederholgenauigkeit am Referenz (uEVR) ist die Unsicherheit aus wiederholten Messungen des Referenzteils durch denselben Bediener mit demselben Gerät. Diese Statistik ist eine Eingabe für die Analyse. In der Regel stammt dieser Wert aus einer Messmittelstudie vom Typ I.
- Auflösung (uRE)
- Die Auflösung (uRE) ist die Unsicherheit aufgrund der Auflösung des Messgeräts. Die Analyse berechnet diese Statistik, wenn die Auflösung des Messgeräts eine Eingabe für die Analyse ist.
- Wiederholbarkeit des Messobjekts (uEVO)
- Die Wiederholbarkeit des Messobjekts (uEVO) ist die Unsicherheit aufgrund der Wiederholbarkeit in der Messsystemanalyse. Wiederholbarkeit ist die Variabilität bei Messungen, wenn derselbe Bediener dasselbe Teil mehrmals misst.
- Systematische Messabweichung (uBI)
- Systematische Messabweichung (uBI) ist die Unsicherheit in den Messungen aufgrund der Differenz zwischen der bekannten Referenzmessung und dem Durchschnitt der Messungen in der Studie. Diese Statistik ist eine Eingabe für die Analyse. In der Regel stammt dieser Wert aus einer Bias-Studie, bei der das Referenzteil innerhalb des Messbereichs liegt.
- Linearität (uLIN)
- Die Linearität (uLIN) ist die Unsicherheit in den Messungen aus der Linearität. Die Linearität ist die Differenz zwischen dem Wert des Referenzteils und der durchschnittlichen Messung, die sich aus der Änderung der Bias ergibt, wenn sich der Wert des Teils ändert. Diese Statistik ist eine Eingabe für die Analyse. In der Regel stammt dieser Wert aus einer Linearitätsstudie, bei der das Referenzteil innerhalb des Messbereichs lag.
- Weitere Faktoren (uREST)
- Weitere Faktoren (uREST) ist die Unsicherheit in den Messungen aufgrund eines oder mehrerer zusätzlicher Faktoren, die nicht in der Studie enthalten sind. Wenn die Spezifikationen für die Analyse einen zusätzlichen Faktor enthalten, dann ist diese Unsicherheit ein Input für die Analyse. Wenn die Angaben für die Analyse mehr als einen Faktor enthalten, der nicht in der Studie enthalten ist, dann kombiniert diese Unsicherheit die Werte. Nehmen wir zum Beispiel an, dass die Temperatur in der Studie keine Rolle spielt, die Messungen jedoch größere Unterschiede aufweisen, wenn die Datenerfassung bei einer höheren Temperatur erfolgt. Verwenden Sie die Angaben für andere Faktoren, um die Unsicherheit aufgrund der Temperatur zu berücksichtigen.
- Prüfer (uAV)
- Prüfer (uAV) ist die Unsicherheit in den Messungen aufgrund der Reproduzierbarkeit in der Messsystemanalyse. Reproduzierbarkeit ist die Variabilität bei Messungen, wenn verschiedene Bediener dasselbe Teil messen.
- Beiträge von Faktoren in der Studie (u gefolgt vom Faktornamen)
- Die Tabelle enthält eine Zeile für jeden zusätzlichen Faktor. In der Zeile wird die Unsicherheit in den Messungen angezeigt, die auf diesen Faktor zurückzuführen ist. Diese Statistik ist die Variabilität der Messungen aufgrund der unterschiedlichen Niveaus des entsprechenden Faktors.
- Wechselwirkungen (uIA)
- Wechselwirkungen (uIA) ist die Unsicherheit in den Messungen aufgrund der Wechselwirkung zwischen Teil und Bediener in der Mess- und Prüftechnikstudie. Die Wechselwirkung befindet sich in der Analyse, wenn eine Wechselwirkung in der ANOVA-Tabelle statistisch signifikant ist. Zu den Wechselwirkungen gehören die Wechselwirkung Teil*Prüfer und alle Interaktionen, die in den Begriffen in der Analyse enthalten sind.
- Messprozess (uMP)
- Der Messprozess (uMP) kombiniert alle Unsicherheitskomponenten, um die Gesamtunsicherheit aus dem Messprozess abzuschätzen.
- % von Gesamt
- Für jede Unsicherheitsquelle wird in der Analyse der Prozentsatz des uMP dargestellt, der sich aus dieser Quelle ergibt. Verwenden Sie den Prozentsatz, um die Unsicherheit aus den verschiedenen Quellen zu vergleichen.
- % der Toleranz (%QMP)
- % der Toleranz (%QMP) kombiniert die Unsicherheit des Messprozesses mit der Variation der Studie und vergleicht den Wert mit der Prozesstoleranz. %QMP ist eine gängige Methode, um zu entscheiden, ob ein Messprozess zufriedenstellend ist. In einigen Anwendungen bedeutet ein Wert von 30 % oder weniger, dass ein Messprozess zufriedenstellend ist.
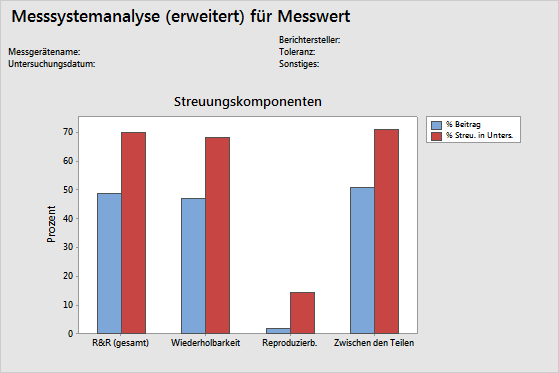
Grafik „Streuungskomponenten“
Die Grafik der Streuungskomponenten stellt eine grafische Zusammenfassung der Ergebnisse einer Messsystemanalyse dar.
- R&R (gesamt): Die Streuung des Messsystems, das mehrere Prüfer umfasst, die dasselbe Messgerät nutzen.
- Wiederholbarkeit: Die Streuung in den Messwerten, wenn dasselbe Teil mehrmals vom selben Prüfer gemessen wird.
- Reproduzierbarkeit: Die Streuung in den Messwerten, wenn verschiedene Prüfer dasselbe Teil messen.
- Zwischen den Teilen: Die Streuung in den Messwerten, die auf verschiedene Teile zurückzuführen ist.
Interpretation
- %Beitrag
- „%Beitrag“ ist der Prozentsatz der einzelnen Varianzkomponenten an der Gesamtstreuung. Dieser Wert wird berechnet, indem die Varianzkomponente der betreffenden Quelle durch die Gesamtstreuung dividiert und anschließend mit 100 multipliziert wird.
- %Streuung in Unters.
- „%Streuung in Unters.“ ist der Prozentsatz der einzelnen Quellen an der Streuung in der Untersuchung. Dieser Wert wird berechnet, indem die Streuung in der Untersuchung für die betreffende Quelle durch die Gesamtstreuung in der Untersuchung dividiert und anschließend mit 100 multipliziert wird.
- %Toleranz
- Mit „%Toleranz“ wird die Streuung des Messsystems mit den Spezifikationen verglichen. „%Toleranz“ wird berechnet, indem die Streuung in der Untersuchung für jede Quelle durch die Prozesstoleranz dividiert und anschließend mit 100 multipliziert wird.
- %Prozess
- Mit „%Prozess“ wird die Streuung des Messsystems mit der Gesamtstreuung verglichen. Dieser Wert wird berechnet, indem die Streuung in der Untersuchung für jede Quelle durch die historische Prozessstreuung dividiert und anschließend mit 100 multipliziert wird.
In einem akzeptablen Messsystem ist die größte Streuungskomponente die Streuung zwischen den Teilen.
X-quer-Karte
Die X-quer-Karte vergleicht die Streuung in den Prüfobjekten mit der Komponente der Wiederholbarkeit.
- Dargestellte Punkte
- Stellen den durchschnittlichen Messwert für jedes Teil angeordnet nach den einzelnen Prüfern dar.
- Mittellinie (X-quer)
- Der Gesamtdurchschnitt für alle Teilemesswerte aller Prüfer.
- Eingriffsgrenzen (UEG und OEG)
- Die Eingriffsgrenzen basieren auf der geschätzten Wiederholbarkeit und der Anzahl der Messungen in jedem Durchschnitt.
Interpretation
Die für eine Messsystemanalyse ausgewählten Teile sollten die gesamte Spannweite der möglichen Teile darstellen. Damit sollte in dieser Grafik eine stärkere Streuung zwischen den Durchschnittswerten der Teile zu beobachten sein, als nach der Streuung aufgrund von Wiederholbarkeit allein zu erwarten wäre.
Im Idealfall weist die Grafik enge Eingriffsgrenzen mit vielen Punkten außer Kontrolle auf, die auf ein Messsystem mit geringer Streuung verweisen.
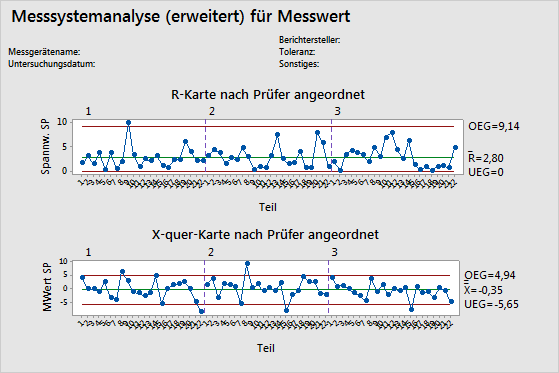
R-Karte
Die R-Karte ist eine Regelkarte der Spannweiten. Sie stellt die Beständigkeit der Prüfer dar.
- Dargestellte Punkte
- Diese stellen für jeden Prüfer die Differenz zwischen dem größten und dem kleinsten Messwert jedes Teils dar. Auf der R-Karte werden die Punkte nach Prüfern angeordnet dargestellt, so dass Sie feststellen können, wie beständig die einzelnen Prüfer messen.
- Mittellinie (R-quer)
- Der Gesamtdurchschnitt für den Prozess (d. h. der Durchschnitt sämtlicher Spannweiten aller Stichproben).
- Eingriffsgrenzen (UEG und OEG)
- Der Betrag der Streuung, der für die Spannweiten der Stichproben erwartet werden kann. Minitab berechnet die Eingriffsgrenzen anhand der Streuung innerhalb der Stichproben.
Hinweis
Wenn jeder Prüfer jedes Teil mindestens neunmal misst, zeigt Minitab anstelle einer R-Karte eine S-Karte an.
Interpretation
Eine kleine durchschnittliche Spannweite zeigt an, dass das Messsystem eine geringe Streuung aufweist. Ein Punkt oberhalb der oberen Eingriffsgrenze (OEG) gibt an, dass der Prüfer die Teile nicht beständig misst. Bei der Berechnung der OEG werden die Anzahl der Messungen pro Teil durch die einzelnen Prüfer sowie die Streuung zwischen den Teilen berücksichtigt. Wenn die Prüfer die Teile beständig messen, ist die Spannweite zwischen dem höchsten und dem niedrigsten Messwert bezogen auf die Streuung in der Untersuchung klein, und die Punkte sollten unter Kontrolle sein.

Diagramm der Messwerte nach einem einzelnen Faktor (Teil) angeordnet
In der Grafik „Nach Teil angeordnet“ werden alle Messwerte nach Teilen angeordnet dargestellt, so dass die Unterschiede zwischen den Teilen ersichtlich werden. In Messsystemanalysen werden Messwerte i. d. R. nach Teil und nach Prüfer angeordnet; bei einer erweiterten Messsystemanalyse können Sie jedoch auch andere Faktoren grafisch darstellen.
In der Grafik stellen die Punkte die Messwerte und die Kreis-Kreuz-Symbole die Mittelwerte dar. Die durchschnittlichen Messwerte für die einzelnen Faktorstufen sind durch eine Verbindungslinie verbunden.
Hinweis
Wenn pro Stufe mehr als 9 Beobachtungen vorliegen, zeigt Minitab ein Boxplot anstelle eines Einzelwertdiagramms an.
Interpretation
Mehrere Messwerte für jedes einzelne Teil, die so wenig wie möglich variieren (die Punkte für ein Teil liegen nah beieinander), verweisen darauf, dass das Messsystem eine geringe Streuung aufweist. Zudem sollten die Durchschnittsmesswerte der Teile ausreichend variieren, um zu zeigen, dass es sich um unterschiedliche Teile handelt und dass diese die gesamte Prozessspannweite darstellen.
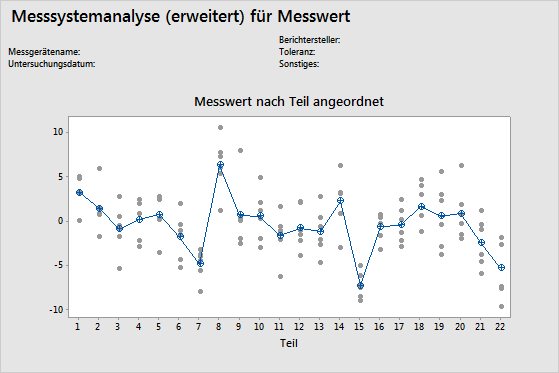
Diagramm der Messwerte nach einem einzelnen Faktor (Prüfer) angeordnet
In der Grafik „Nach Prüfer angeordnet“ werden alle Messwerte nach Prüfern angeordnet dargestellt, so dass die Unterschiede zwischen den Prüfern ersichtlich werden. In Messsystemanalysen werden Messwerte i. d. R. nach Teil und nach Prüfer angeordnet; bei einer erweiterten Messsystemanalyse können Sie jedoch auch andere Faktoren grafisch darstellen.
Hinweis
Wenn pro Prüfer weniger als 10 Beobachtungen vorliegen, zeigt Minitab kein Boxplot, sondern ein Einzelwertdiagramm an.
Interpretation
Eine horizontale Gerade über verschiedene Prüfer hinweg zeigt, dass die mittleren Messwerte für jeden Prüfer gleich sind. Im Idealfall variieren die Messwerte für jeden Prüfer um den gleichen Beitrag.
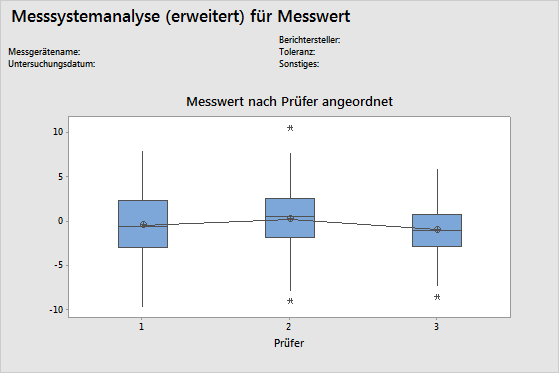
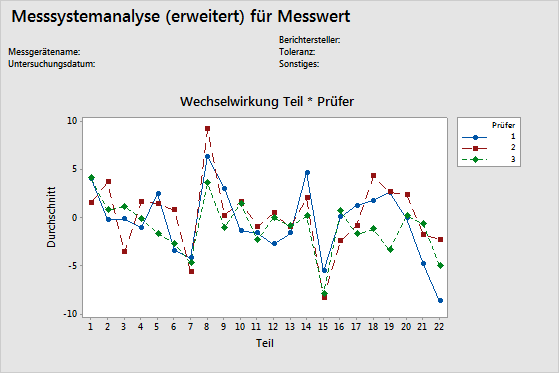
Diagramm der Wechselwirkung (Prüfer*Teil)
Im Diagramm der Wechselwirkung Prüfer*Teil werden die durchschnittlichen Messwerte der einzelnen Prüfer für jedes Teil angezeigt. Messsystemanalysen enthalten in der Regel Wechselwirkungen zwischen Prüfer und Teil, bei einer erweiterten Messsystemanalyse können Sie jedoch auch andere Wechselwirkungen grafisch darstellen.
In einem Wechselwirkungsdiagramm wird die Wechselwirkung zwischen zwei Faktoren veranschaulicht. Eine Wechselwirkung liegt vor, wenn der Effekt eines Faktors von einem zweiten Faktor abhängt. Dieses Diagramm ist die grafische Entsprechung des F-Tests für einen Wechselwirkungsterm in der ANOVA-Tabelle.
Jede Linie verbindet die Durchschnittswerte für einen einzelnen Prüfer (oder für einen anderen Term, den Sie angeben).
Interpretation
Zusammenfallende Linien zeigen an, dass die Prüfer gleich messen. Linien, die nicht parallel verlaufen oder einander schneiden, verweisen darauf, dass die Fähigkeit eines Prüfers, ein Teil beständig zu messen, vom jeweils gemessenen Teil abhängt. Eine Linie, die durchgehend höher oder niedriger als die übrigen liegt, zeigt an, dass ein Prüfer eine systematische Messabweichung beiträgt, indem er beständig zu hohe oder zu niedrige Messwerte erfasst.