In diesem Thema
Varianzkomponenten
Das Diagramm Beitrag der Varianzkomponenten und die Tabelle Varianzkomponenten zeigen die Streuung aus verschiedenen Quellen.
Interpretation
Verwenden Sie die Varianzkomponenten, um die Streuung aus jeder Quelle zu bewerten. Die Test-Retest-Varianz und die Operator-Varianz sind Messfehler. Die Teilevariation stellt den Bereich der Teile in der Studie dar. Die Gesamtvarianz ist die Summe der anderen Komponenten. Wenn die Analyse die Wechselwirkung einschließt, hängt die Höhe des Messfehlers davon ab, welches Teil ein Prüfer misst.
In einem akzeptablen Messsystem ist die größte Variationskomponente die Teilevariation. Wenn Test-Retest-Variation und Operator-Variation große Mengen an Variation beitragen, untersuchen Sie die Ursache des Problems und ergreifen Sie Korrekturmaßnahmen.
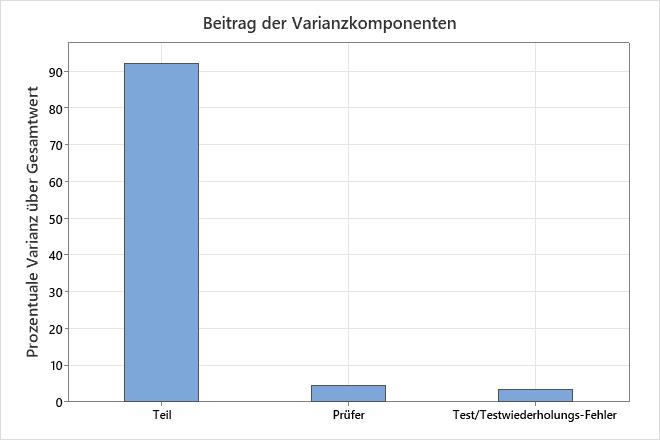
Varianzkomponenten
| Quelle | Varianz | %Gesamt | StdAbw |
|---|---|---|---|
| Test/Testwiederholungs-Fehler (Wiederholbarkeit) | 0,03997 | 3,394 | 0,19993 |
| Prüfer (Reproduzierbarkeit) | 0,05146 | 4,368 | 0,22684 |
| Teil (Produktstreuung) | 1,08645 | 92,238 | 1,04233 |
| Gesamt | 1,17788 | 100,000 | 1,08530 |
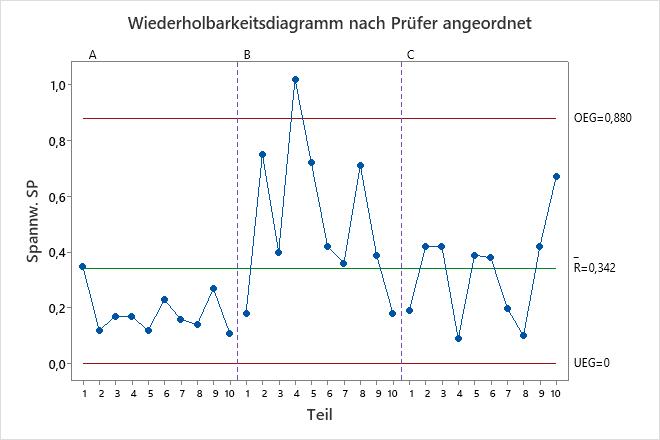
Wiederholbarkeitsdiagramm
Das Wiederholbarkeitsdiagramm ist eine Regelkarte mit Bereichen, die die Operatorkonsistenz anzeigt.
- Dargestellte Punkte
- Für jeden Prüfer ist der Stichprobenbereich die Differenz zwischen den größten und kleinsten Messungen jedes Teils. Verwenden Sie die Beispielbereiche, um die Operatorkonsistenz zu bewerten.
- Mittellinie (R-quer)
- Der Gesamtdurchschnitt für den Prozess (d. h. der Durchschnitt sämtlicher Spannweiten aller Stichproben).
- Eingriffsgrenzen (UEG und OEG)
- Der Betrag der Streuung, der für die Spannweiten der Stichproben erwartet werden kann. Minitab berechnet die Eingriffsgrenzen anhand der Streuung innerhalb der Stichproben.
Hinweis
Wenn jeder Operator jedes Teil 9 Mal oder öfter misst, zeigt Minitab im Diagramm Standardabweichungen anstelle von Bereichen an.
Interpretation
Je kleiner der Durchschnittsbereich, desto geringer die Abweichung vom Messsystem. Ein Punkt oberhalb der oberen Eingriffsgrenze (OEG) gibt an, dass der Prüfer die Teile nicht beständig misst. Die Berechnung der OEG umfasst die Anzahl der Messungen pro Teil durch jeden Prüfer und die Teilevariation. Wenn die Prüfer die Teile beständig messen, ist die Spannweite zwischen dem höchsten und dem niedrigsten Messwert bezogen auf die Streuung in der Untersuchung klein, und die Punkte sollten unter Kontrolle sein.
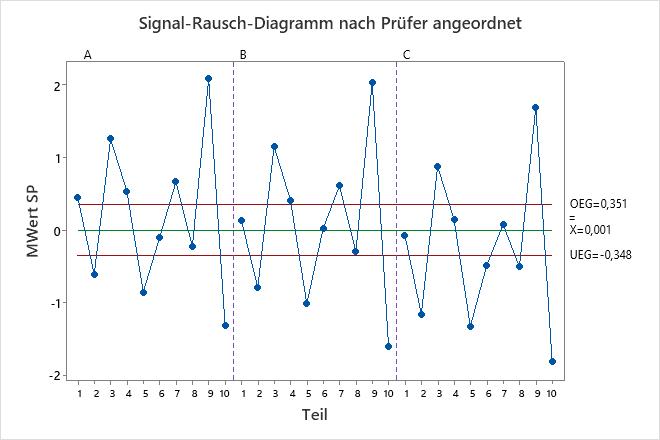
Signal-Rausch-Diagramm nach Prüfer angeordnet
Das Diagramm vergleicht die Teilevariation mit der Test-Retest-Komponente.
- Dargestellte Punkte
- Stellen den durchschnittlichen Messwert für jedes Teil angeordnet nach den einzelnen Prüfern dar.
- Mittellinie (
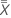 )
) - Der Gesamtdurchschnitt für alle Teilemesswerte aller Prüfer.
- Eingriffsgrenzen (UEG und OEG)
- Die Eingriffsgrenzen basieren auf der geschätzten Wiederholbarkeit und der Anzahl der Messungen in jedem Durchschnitt.
Interpretation
Die Teile, die für eine Studie ausgewählt werden, sollten die gesamte Bandbreite möglicher Teile repräsentieren. Daher sollte dieses Diagramm eine größere Variation zwischen den Teiledurchschnitten anzeigen, als von der Test-Retest-Variation allein erwartet wird.
Im Idealfall weist die Grafik enge Eingriffsgrenzen mit vielen Punkten außer Kontrolle auf, die auf ein Messsystem mit geringer Streuung verweisen.
Parallelitätsdiagramm
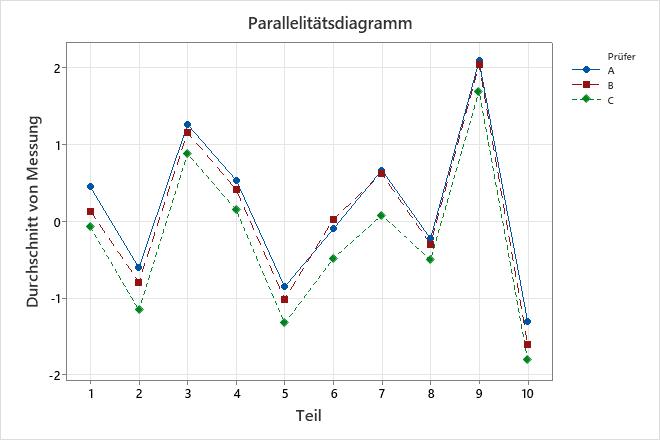
Das Parallelitätsdiagramm zeigt die durchschnittlichen Messwerte der einzelnen Prüfer für jedes Teil an. Jede Linie verbindet die Durchschnitte für jeden einzelnen Prüfer.
Das Diagramm zeigt die Interaktion zwischen zwei Variationsquellen: Teilen und Prüfer. Eine Wechselwirkung liegt vor, wenn der Effekt eines Faktors von einem zweiten Faktor abhängt.
Interpretation
Zusammenfallende Linien zeigen an, dass die Prüfer gleich messen. Linien, die nicht parallel verlaufen oder einander schneiden, verweisen darauf, dass die Fähigkeit eines Prüfers, ein Teil beständig zu messen, vom jeweils gemessenen Teil abhängt. Eine Linie, die durchgehend höher oder niedriger als die übrigen liegt, zeigt an, dass ein Prüfer eine systematische Messabweichung beiträgt, indem er beständig zu hohe oder zu niedrige Messwerte erfasst.
Analyse der Haupteffekte (ANOME) Diagramm
Das Diagramm vergleicht die durchschnittlichen Messwerte für die Operatoren.
- Dargestellte Punkte
- Die durchschnittliche Messung aller Teile für jeden Prüfer.
- Mittellinie (Durchschnitt)
- Der Gesamtdurchschnitt für alle Teilemesswerte aller Prüfer.
- Entscheidungsgrenzen (UEG und OEG)
- Die Grenzwerte basieren auf der Test-Retest-Schätzung und der Anzahl der Messungen in jedem Mittelwert.
Interpretation
Punkte außerhalb der Entscheidungsgrenzen weisen darauf hin, dass verschiedene Operatoren den Messungen eine Verzerrung hinzufügen. Im Idealfall liegen die Punkte alle innerhalb der Entscheidungsgrenzen, um anzuzeigen, dass die Gesamtdurchschnitte der Operatoren ähnlich sind.
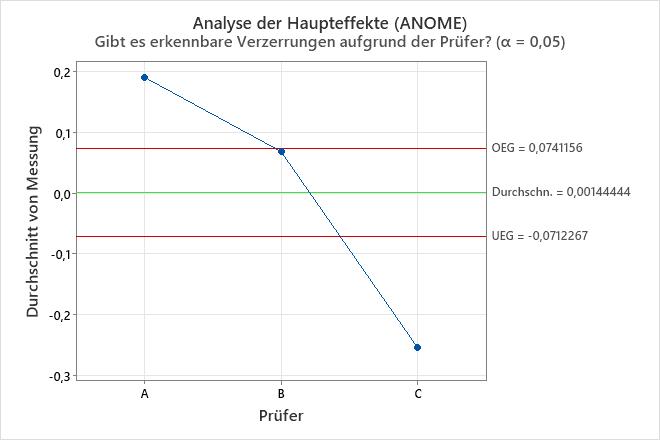
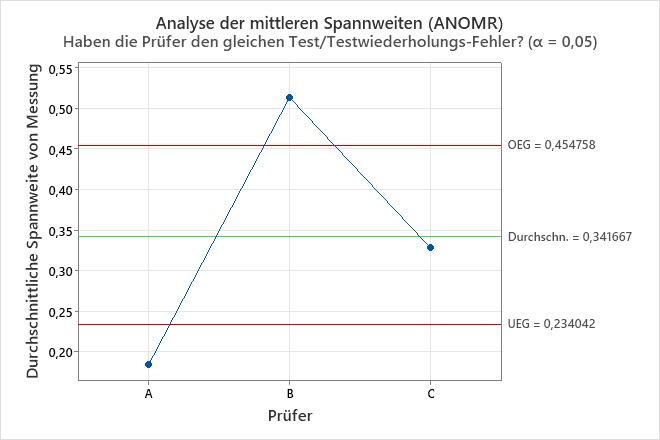
Diagramm der Analyse der mittieren Spannweiten (ANOMR)
Das Diagramm vergleicht den durchschnittlichen Messbereich für die Prüfer.
- Dargestellte Punkte
- Der Durchschnitt der Messbereiche für jedes Teil für jeden Operator.
- Mittellinie (Durchschnitt)
- Der Gesamtdurchschnitt für alle Bereiche von allen Betreibern.
- Entscheidungsgrenzen (UEG und OEG)
- Die Grenzwerte basieren auf der Test-Retest-Schätzung.
Interpretation
Punkte außerhalb der Entscheidungsgrenzen zeigen an, dass einige Operatoren mehr oder weniger konsistent messen als andere Operatoren. Im Idealfall liegen die Punkte alle innerhalb der Entscheidungsgrenzen, um anzuzeigen, dass die Gesamtbereiche der Operatoren ähnlich sind.
MPA-Statistiken und Klassifikationsrichtlinien
Die MPA-Statistik klassifiziert das Messsystem von der besten Bewertung der ersten Klasse bis zur schlechtesten Bewertung der vierten Klasse. Die Klassen entsprechen dem klasseninternen Korrelationskoeffizienten. In der Praxis erklärt der Koeffizient, wie gut das Messsystem eine Verschiebung des Prozessmittelwerts von mindestens 3 Standardabweichungen erkennt. Messsysteme erster und zweiter Klasse haben in der Regel eine hohe Wahrscheinlichkeit, solche Verschiebungen mit einer begrenzten Anzahl von Tests und Untergruppen auf einer Regelkarte zu erkennen. Bei Messsystemen dritter Klasse fügt die typische Analyse der Regelkarte Tests hinzu, um die Wahrscheinlichkeit zu erhöhen, eine Verschiebung des Prozessmittelwerts zu erkennen. Ein Messsystem vierter Klasse muss in der Regel verbessert werden, um einen Prozess zu überwachen oder um Aktivitäten zur Prozessverbesserung durchzuführen.
Die Klassifizierung bezieht sich auch auf die Dämpfung von Signalen aus dem Prozess. Die Dämpfung ist der Betrag der Änderung, der mit dem Messfehler verwechselt wird. Bei einem Messsystem, das 50 % einer Änderung abschwächt, wird eine Änderung von 2 Standardabweichungen wahrscheinlich als Änderung von 1 Standardabweichung angezeigt.
- Test-Retest-Fehler
- Die Variabilität der Messungen, wenn derselbe Prüfer dasselbe Teil mehrmals misst. Je kleiner der Wert, desto besser schneidet das Messsystem ab.
- Freiheitsgrade
- Die Freiheitsgrade (DF) für die Schätzung des Test-Retest-Fehlers. Im Allgemeinen misst DF, wie viele Informationen zur Berechnung des Fehlers zur Verfügung stehen.
- Wahrscheinlicher Fehler
- Die Unsicherheit für eine einzelne Messung. Bei der Analyse wird der wahrscheinliche Fehler mit dem Messinkrement in der Tabelle "Effektive Auflösung der Messwerte" verglichen, um festzustellen, ob die Genauigkeit der Messwerte vertrauenswürdig ist. Wheeler (2006) 1 Beschreibt Methoden zur Verwendung des wahrscheinlichen Fehlers zur Bestimmung von Spezifikationsgrenzen für einen Prozess unter Berücksichtigung der Leistung des Messsystems.
- Intraklassen-Korrelation
- Der klasseninterne Korrelationskoeffizient vergleicht die Gesamtvariation mit der Teilevariation. Werte, die näher an 1 liegen, weisen auf eine geringere Abweichung vom Messsystem hin.
- Keine Voreingenommenheit
- Ohne Verzerrung beschreibt der Koeffizient, wie gut das Messsystem funktioniert, wenn alle Prüfer die Teile im Durchschnitt gleich messen.
- Mit Voreingenommenheit
- Bei der Verzerrung beschreibt der Koeffizient, wie gut das Messsystem bei Unterschieden zwischen den Prüfern abschneidet.
- Mit Voreingenommenheit und Interaktion
- Wenn bei der Analyse festgestellt wird, dass verschiedene Operatoren unterschiedliche Teile unterschiedlich messen, enthalten die Ergebnisse die klasseninterne Korrelation mit Verzerrung und Interaktion. Der Koeffizient beschreibt, wie gut das Messsystem funktioniert, wenn verschiedene Prüfer verschiedene Teile unterschiedlich messen.
- Auswirkungen von Verzerrungen
- Die Differenz zwischen dem Intraklassenkoeffizienten mit und ohne Verzerrung. Je kleiner der Wert, desto weniger tragen die Unterschiede der Prüfer zur Variation der Messungen bei.
- Verzerrungen und Interaktionseffekte
- Die Differenz zwischen dem klasseninternen Koeffizienten mit Bias und Interaktion und dem Koeffizienten ohne Verzerrung. Je kleiner der Wert, desto weniger tragen Unterschiede in der Art und Weise, wie verschiedene Prüfer die verschiedenen Teile messen, zur Variation der Messungen bei.
MPA-Statistiken
| Statistik | Wert | Klassifikation |
|---|---|---|
| Test/Testwiederholungs-Fehler | 0,1999 | |
| Freiheitsgrade | 78,0000 | |
| Wahrscheinlicher Fehler | 0,1349 | |
| Intraklassen-Korrelation (keine Verzerrung) | 0,9645 | Erste Klasse |
| Intraklassen-Korrelation (mit Verzerrung) | 0,9224 | Erste Klasse |
| Auswirkung der Verzerrung | 0,0421 |
Klassifikationsrichtlinien
| Klassifikation | Intraklassen-Korrelation | Dämpfung der Prozesssignale | Warnwahrscheinlichkeit, Test 1* |
|---|---|---|---|
| Erste Klasse | 0,80 - 1,00 | Weniger als 11% | 0,99 - 1,00 |
| Zweite Klasse | 0,50 - 0,80 | 11 - 29% | 0,88 - 0,99 |
| Dritte Klasse | 0,20 - 0,50 | 29 - 55% | 0,40 - 0,88 |
| Vierte Klasse | 0,00 - 0,20 | Mehr als 55% | 0,03 - 0,40 |
| Klassifikation | Warnwahrscheinlichkeit, Tests* |
|---|---|
| Erste Klasse | 1,00 |
| Zweite Klasse | 1,00 |
| Dritte Klasse | 0,92 - 1,00 |
| Vierte Klasse | 0,08 - 0,92 |
Effektive Auflösung der Messwerte
Die Statistiken über die Auflösung beschreiben, wie sehr Sie der aufgezeichneten Genauigkeit der Messungen vertrauen können.
- Wahrscheinlicher Fehler (PE)
- Die Unsicherheit für eine einzelne Messung. Bei der Analyse wird der wahrscheinliche Fehler mit dem Messinkrement in der Tabelle "Effektive Auflösung der Messwerte" verglichen, um festzustellen, ob die Genauigkeit der Messwerte vertrauenswürdig ist. Wheeler (2006)1 beschreibt Methoden zur Verwendung des wahrscheinlichen Fehlers zur Bestimmung von Spezifikationsgrenzen für einen Prozess unter Berücksichtigung der Leistungsfähigkeit des Messsystems.
- Untere Grenze des Inkrements (0,1 * PE)
- Eine Untergrenze dafür, wann das Messinkrement vertrauenswürdig ist. Wenn das Messinkrement kleiner als die Untergrenze des Inkrements ist, sollten Sie unbedingt überlegen, ob die Messungen mit geringerer Genauigkeit aufgezeichnet werden sollen.
- Kleinstes effektives Inkrement (0,22 * PE)
- Eine Schätzung, wie genau das System wahrscheinlich eine Messung durchführen wird. Wenn das Messinkrement kleiner als das kleinste effektive Inkrement ist, überlegen Sie, ob die Messungen mit geringerer Genauigkeit aufgezeichnet werden sollen.
- Aktuelles Messinkrement
- Eine Schätzung aus den Daten oder ein angegebener Wert, der erklärt, wie genau die aufgezeichneten Messungen sind. Für die Werte 1,1, 1,4 und 1,9 wird bei der Analyse beispielsweise ermittelt, dass das Inkrement 0,1 beträgt, da die Messungen die Zehntelstelle enthalten.
- Größtes effektives Inkrement (2,2 * PE)
- Eine Schätzung, wie genau das System wahrscheinlich eine Messung durchführen wird. Wenn das Messinkrement größer als das größte effektive Inkrement ist, überlegen Sie, ob die Messungen genauer aufgezeichnet werden sollen.
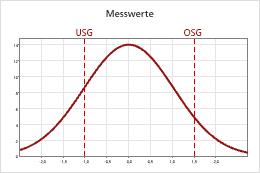
Wahrscheinlichkeiten der Fehlklassifikation
Wenn Sie mindestens eine Spezifikationsgrenze angeben, kann Minitab die Wahrscheinlichkeiten der Fehlklassifikation eines Produkts berechnen. Aufgrund der Streuung des Messsystems ist der gemessene Wert des Teils nicht immer gleich dem tatsächlichen Wert. Der Unterschied zwischen dem gemessenen Wert und dem tatsächlichen Wert bringt die Möglichkeit der Fehlklassifikation des Teils mit sich.
- Verbundene Wahrscheinlichkeit
- Wählen Sie die verbundene Wahrscheinlichkeit aus, wenn noch keine Erkenntnisse über die Annehmbarkeit der Teile vorliegen. Sie nehmen beispielsweise Stichproben von der Fertigungslinie und wissen nicht, ob ein bestimmtes Teil gut oder schlecht ist. Es gibt zwei Fehlklassifikationen, die Sie machen können:
- Die Wahrscheinlichkeit, dass das Teil schlecht ist, Sie es aber annehmen.
- Die Wahrscheinlichkeit, dass das Teil gut ist, Sie es aber ablehnen.
- Bedingte Wahrscheinlichkeit
- Verwenden Sie die bedingte Wahrscheinlichkeit, wenn bereits Erkenntnisse über die Annehmbarkeit der Teile vorliegen. Sie entnehmen zum Beispiel Stichproben von einem Stapel, der nachbearbeitet werden muss, oder von einem Stapel, dessen Produkte für gut befunden wurden und in Kürze ausgeliefert werden sollen. Es gibt zwei Fehlklassifikationen, die Sie machen können:
- Die Wahrscheinlichkeit, dass Sie ein Teil annehmen, das als Stichprobe aus einem Stapel schlechter Produkte gezogen wurde, der nachbearbeitet werden muss (auch als falsche Annahme bezeichnet).
- Die Wahrscheinlichkeit, dass Sie ein Teil zurückweisen, das als Stichprobe aus einem Stapel guter Produkte gezogen wurde, der zur Lieferung ansteht (auch als falsche Rückweisung bezeichnet).
Interpretation
Verbundene Wahrscheinlichkeiten einer Fehlklassifikation
| Beschreibung | Wahrscheinlichkeit |
|---|---|
| Ein zufällig ausgewähltes Teil ist schlecht, wird aber akzeptiert | 0,037 |
| Ein zufällig ausgewähltes Teil ist gut, wird aber zurückgewiesen | 0,055 |
Bedingte Wahrscheinlichkeiten einer Fehlklassifikation
| Beschreibung | Wahrscheinlichkeit |
|---|---|
| Ein Teil aus einer Gruppe von schlechten Produkten wird akzeptiert | 0,151 |
| Ein Teil aus einer Gruppe von guten Produkten wird zurückgewiesen | 0,073 |
Die verbundene Wahrscheinlichkeit, dass ein Teil schlecht ist und Sie es annehmen, beträgt 0,037. Die verbundene Wahrscheinlichkeit, dass ein Teil gut ist und Sie es zurückweisen, beträgt 0,055.
Die bedingte Wahrscheinlichkeit einer falschen Annahme, also dass Sie ein Teil bei der Nachprüfung annehmen, während es tatsächlich nicht den Spezifikationen entspricht, beträgt 0,151. Die bedingte Wahrscheinlichkeit einer falschen Rückweisung, also dass Sie ein Teil bei der Nachprüfung zurückweisen, während es tatsächlich den Spezifikationen entspricht, beträgt 0,073.
